
laba 3 vt
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ОБНИНСКИЙ ИНСТИТУТ АТОМНОЙ ЭНЕРГЕТИКИ ─ филиал Федерального государственного автономного образовательного высшего профессионального образования
«Национальный исследовательский ядерный университет МИФИ»
(ИАТЭ НИЯУ МИФИ)
Отделение интеллектуальных кибернетических систем
Лабораторная работа №3
По дисциплине
Моделирование систем ВТ
На тему
«Расчет надежности системы.»
Выполнил студент
группы ИВТ-Б17
Петровский В.Б.
Проверил:
Перегуда А.И.
Цель работы:
1. Построить структурную схему;
2. Найти множество минимальных путей и минимальных сечений;
3. Оценить вероятность безотказной работы системы и элементов системы или вероятность отказа.
Постановка задачи: Оценить показатели надежности системы методом Монте-Карло.
Теория:
Опишем общую схему применения методов Монте-Карло к рассматриваемой задаче. Для оценки надежности сети методом Монте-Карло нам нужно случайным образом сгенерировать определенное число реализаций сети, усреднить по полученной выборке интересующий нас показатель и получить таким образом оценку показателя надежности. Данный метод можно представить в виде:
1) моделирование на ЭВМ псевдослучайных последовательностей с заданным законом распределения вероятностей, имитирующих случайные значения параметров при каждом испытании;
2) использование полученных числовых последовательностей в имитационных математических моделях.
3) статистическая обработка результатов моделирования.
Минимальным путем называется последовательный минимальный набор работоспособных элементов данной системы, который обеспечивает функционирование системы, а отказ любого одного из этих элементов приводит к отказу системы.
Минимальным сечением называется последовательный набор неработоспособных элементов, который приводит к отказу системы, а восстановление одного из них приводит к восстановлению работоспособности всей системы.
Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки не произойдет ни одного отказа.
Вероятность безотказной работы обозначается как P(l), которая определяется по формуле:
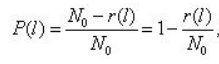
где N0 – число элементов в начале испытания; r(l) – число отказов элементов к моменту наработки.Следует отметить, что чем больше величина N0, тем с большей точностью можно рассчитать вероятность P(l).
Основными достоинствами использования данного показателя при расчетах является два фактора: во-первых, вероятность безотказной работы охватывает все факторы, влияющие на надежность элементов, позволяя достаточно просто судить о его надежности, т.к. чем больше величина P(l), тем выше надежность; во-вторых, вероятность безотказной работы может быть использована в расчетах надежности сложных систем, состоящих из более чем одного элемента.
Интенсивность отказов представляет собой условную плотность возникновения отказа объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказ не возник. Иначе интенсивность отказов – это отношение числа отказавших элементов в единицу времени или пробега к числу исправно работающих элементов в данный отрезок времени.
Схема:
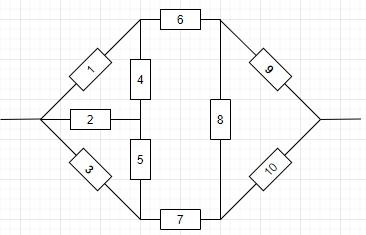
Рисунок 1 – Структурный вид схемы
|
Минимальные пути схемы |
Минимальные сечения: |
|
|
Структурная функция (эквивалентная схема путей):
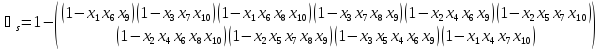
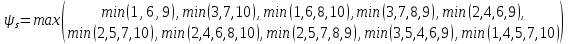
Вероятности отказа элементов системы подчиняются следующим законам:
-
Элементы 1,6,9 – экспоненциальный закон распределения
-
Элементы 3,7,10 – закон распределения Вейбулла-Гнеденко
-
Элементы 2,4,5,8 – закон гамма распределения.
Входные параметры:
Для каждого элемента параметры распределения:
-
Экспоненциальный закон распределения: 𝜆=0.5
-
закон распределения Вейбулла-Гнеденко: a=1.5 b=2.5
-
Гамма распределение: 𝜆=0.7 ,
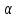 =0.3
=0.3
Число опытов N=5000.
Алгоритм построения гистограммы:
а) Сортировка полученной выборки случайных чисел по возрастанию;
б) определяем количество интервалов (L) по формуле:
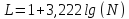 ,
где N
- объем выборки.
,
где N
- объем выборки.
в) Определяем размах выборки(R), как разницу максимального и минимального случайного числа в выборке;
г)
Определяем длину интервала(h)
по формуле:
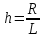 ;
;
д) Для каждого интервала определяем количество сгенерированных чисел, попавших в интервал;
е) Определяем относительные частоты для каждого интервала, как отношение количества попавших в этот интервал сгенерированных чисел к объему выборки.
Проверка выборки на соответствие распределению:
Для
проверки воспользуемся Критерием
Пирсона(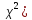 .
.
Алгоритм проверки следующий:
а)
Для каждого интервала разбиения
определяем
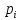 , как
, как
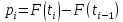 ;
;
б) Сначала определяем меру расхождения(H) по формуле:
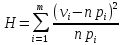 ,
где n
- объем выборки, m
- число интервалов разбиения вариационного
ряда,
,
где n
- объем выборки, m
- число интервалов разбиения вариационного
ряда,
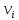 - число членов вариационного ряда,
попавших в i-ый интервал
- число членов вариационного ряда,
попавших в i-ый интервал
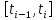 ,
,
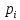 -
вероятность того, что наработка на
отказ примет значение в пределах i-ого
интервала при данном виде функции
распределения.
-
вероятность того, что наработка на
отказ примет значение в пределах i-ого
интервала при данном виде функции
распределения.
в)
По таблицы определяем значение квантили
 ;
;
г) Сравниваем квантиль с мерой расхождения, если мера расхождения меньше квантили, то считаем, что наша выборка соответствует распределению. Если же мера расхождения много больше квантили, то выборка не соответствует распределению, следовательно, нужно заменить способ генерации выборки случайных чисел.
Ход работы:
Использовал язык программирования Python. Для получения случайных чисел r использовал модуль random, встроенный в программную оболочку языка.
Листинг кода программы:
import random as r
import math as m
from scipy import stats
from scipy import special
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
lamda = 0.8
mu1 = 3
lamda1 = 0.4
mu = 3
sigma = 1
#функции
def expF(x):
return 1-m.exp(-lamda*x)
def koshiF(x):
return 0.5+1/3.14*m.atan((x-mu1)/lamda1)
def normalF(x):
return 0.5*(1+special.erf((x-mu)/sigma/m.sqrt(2)))
#плотности
def exp(x):
return lamda*m.exp(-lamda*x)
def koshi(x):
return lamda1/(3.14*(lamda1**2+(x-mu1)**2))
def normal(x):
sq2pi = m.sqrt(2*m.pi)
return 1/(sigma*sq2pi)*m.exp(-m.pow((x-mu),2)/2/sigma/sigma)
def lognormalCheck(x, muC, sigmaC):
sq2pi = m.sqrt(2*m.pi)
return 1/(sigmaC*sq2pi)*m.exp(-m.pow((x-muC),2)/2/sigmaC/sigmaC)
#генерация чисел
def expG(x):
return -1/lamda*m.log(x)
def koshiG(x):
return mu1+lamda1*m.tan(2*3.14*x)
def normalG(X):
return np.random.normal(mu, sigma)
def plotE(bins, vals):
left,right = bins[:-1],bins[1:]
X = np.array([left,right]).T.flatten()
Y = np.array([vals,vals]).T.flatten()
plt.plot(X,Y)
plt.show()
return
bins = []
for i in range(600):
bins.append(i/100)
bins = np.array(bins)
width = 0.8 * (bins[1] - bins[0])
center = (bins[:-1] + bins[1:]) / 2 - width/2
val = []
for value in center:
val.append(normalF(value))
val = np.array(val)
plotE(bins, val)
val = []
for value in center:
val.append(normal(value))
val = np.array(val)
plotE(bins, val)
val = []
for value in center:
val.append(expF(value))
val = np.array(val)
plotE(bins, val)
val = []
for value in center:
val.append(exp(value))
val = np.array(val)
plotE(bins, val)
val = []
for value in center:
val.append(koshiF(value))
val = np.array(val)
plotE(bins, val)
val = []
for value in center:
val.append(koshi(value))
val = np.array(val)
plotE(bins, val)
tau = []
L = int(1 + 3.222 * m.log(5000, 10))
for i in range(5000):
y1 = normalG(r.random())
y2 = normalG(r.random())
y3 = expG(r.random())
y4 = expG(r.random())
y5 = normalG(r.random())
y6 = normalG(r.random())
y7 = koshiG(r.random())
y8 = expG(r.random())
y9 = expG(r.random())
y10 = koshiG(r.random())
y11 = koshiG(r.random())
tau.append(max(min(y1,y8,y9),min(y1,y5,y10,y11),min(y1,y6,y10,y11),
min(y2,y8,y9),min(y2,y5,y10,y11),min(y2,y6,y10,y11),min(y3,y4,y10,y11),
min(y3,y7,y11),min(y3,y4,y5,y8,y9),min(y3,y4,y5,y8,y9)))
p, x = np.histogram(tau, bins=L)
pf = []
for i in range(L):
pf.append(float(p[i]) / 5000.0)
plotE(x,pf)
cumulative = []
cumulative.append(pf[0]);
for i in range(1,len(pf)):
cumulative.append(pf[i]+cumulative[i-1])
plotE(x, cumulative)
width = 0.9 * (x[1] - x[0])
center = (x[:-1] + x[1:]) / 2 - width/2
plt.bar(center, pf, align='center', width=width)
plt.show()
mTau = 0
dTau = 0
for i in range(L):
mTau += x[i]*p[i]
mTau /= 5000
for i in range(L):
dTau += (x[i] - mTau) * (x[i] - mTau)
dTau/=L
dTau=m.sqrt(dTau)
print(L)
print("X:", mTau)
print("sigma:",dTau)
tal99=2.5582
tal975=2.1791
tal95=1.6821
tal90=1.2715
tal80=0.7649
tal60=0.2298
tal55=0.1134
print("P=0.80:")
print("left:", mTau-tal90*dTau/m.sqrt(L-1))
print("right:", mTau+tal90*dTau/m.sqrt(L-1))
expected = []
for i in range(L):
expected.append(lognormalCheck(x[i], mTau, dTau))
print("Chi-square:",stats.chisquare(pf, expected))
iofunc = []
x = []
y = []
y.append(expG(r.random()))
y.append(koshiG(r.random()))
y.append(normalG(r.random()))
y.append(koshiG(r.random()))
y.append(koshiG(r.random()))
y.append(normalG(r.random()))
y.append(expG(r.random()))
y.append(koshiG(r.random()))
y.append(normalG(r.random()))
y.append(expG(r.random()))
y.append(koshiG(r.random()))
y.append(normalG(r.random()))
for i in range(1,10001):
broken=0
for j in range(9):
if (i/2000 > y[j]):
broken+=1
if broken != 0:
x.append(i/2000)
if broken != 9:
iofunc.append(broken/i*2000/(9-broken))
else:
iofunc.append(4)
plt.plot(x,iofunc)
plt.show()
Моделирование случайных величин:
-
Экспоненциальный закон распределения:
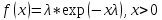
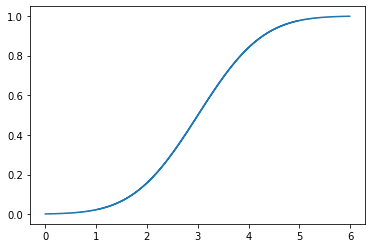
Рисунок 3 – Функция распределения
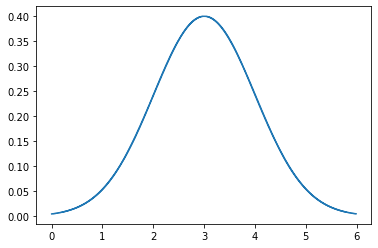
Рисунок 4 – Плотность вероятности
-
Распределение Коши:
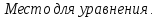
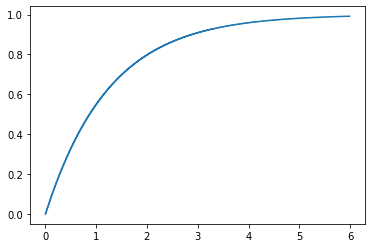
Рисунок 5 – Функция распределения
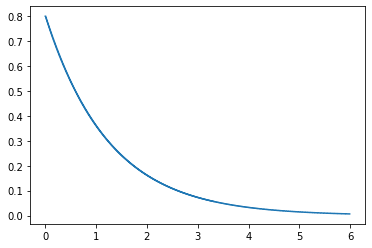
Рисунок 6 – Плотность вероятности
-
Нормальный закон распределения:
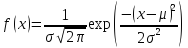
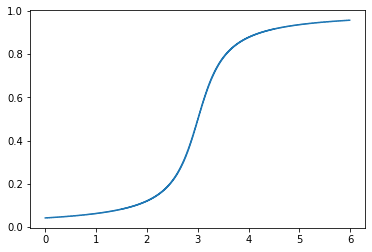
Рисунок 7 – Функция распределения
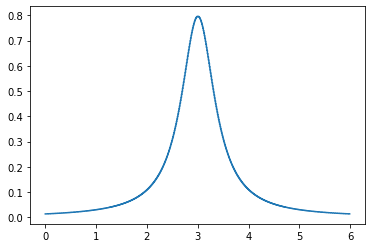
Рисунок 8 – Плотность вероятности
Получившееся распределение:
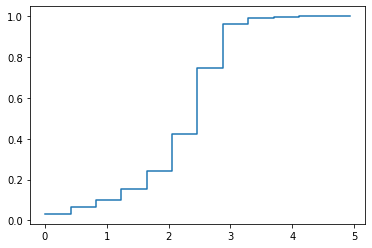
Рисунок 9 – Эмпирическая функция распределения
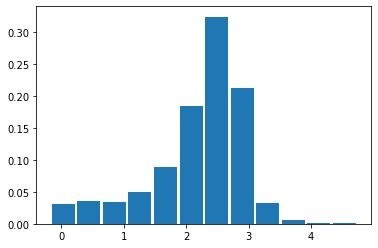
Рисунок 10 – Гистограмма
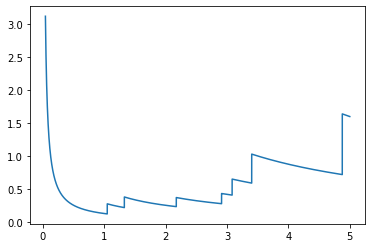
Рисунок 11 – Интенсивность отказов
По полученным графикам можем сделать вывод о полученном распределении. Это логнормальное распределение, что подтвердим с помощью критерия хи квадрат.

Данная выборка подчиняется логнормальному закону распределения.
Математическое ожидание: 2.174
Интервал, верхнее и нижнее значение, в котором находится мат. ожидание: от 1.591 до 2.757
Среднеквадратичное сигма получилось равным: 1.417
Вероятность безотказной работы P=0.80
Из графика интенсивности отказов мы можем сделать вывод о том, что в первый момент времени выходят из строя бракованные элементы, следом идет низкая интенсивность отказов, а именно рабочая нагрузка система. После чего из-за эффекта старения количество отказов возрастает.
Вывод: смоделировав вычисления показателей надёжности технической системы с помощью метода Монте-Карло, я получил, что при заданных параметрах система подчиняется логнормальному распределению, а также вычислил необходимые характеристики системы. Интенсивность отказов данной системы находится на достаточном уровне, учитывая количество проведенных испытаний.
Обнинск 2019
