2.2. Случайная величина непрерывного типа. Плотность вероятности распределения случайной величины

Определение 2.2.1. Случайная величина Х называется случайной величиной непрерывного типа, если существует неотрицательная функция f(x), определенная на (- , ) и такая, что функция распределения F(x) имеет вид

F(x) = 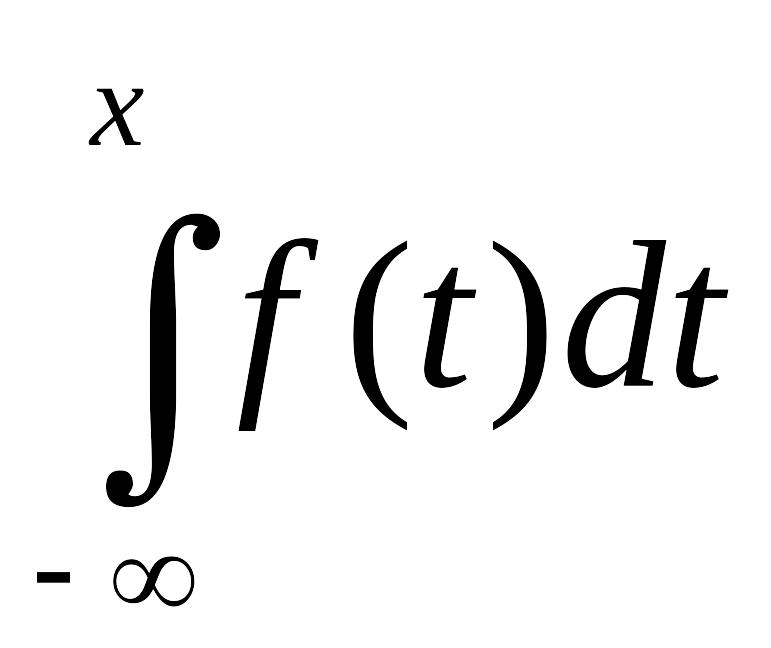, –∞ < x < ∞. (2.2.1)

Функция f(x) называется плотностью вероятности случайной величины или плотностью распределения случайной величины.

В отличие от случайной величины дискретного типа случайная величина непрерывного типа принимает несчетное множество значений.

Свойства плотности вероятности

Свойство 1. Р(x₁ X < x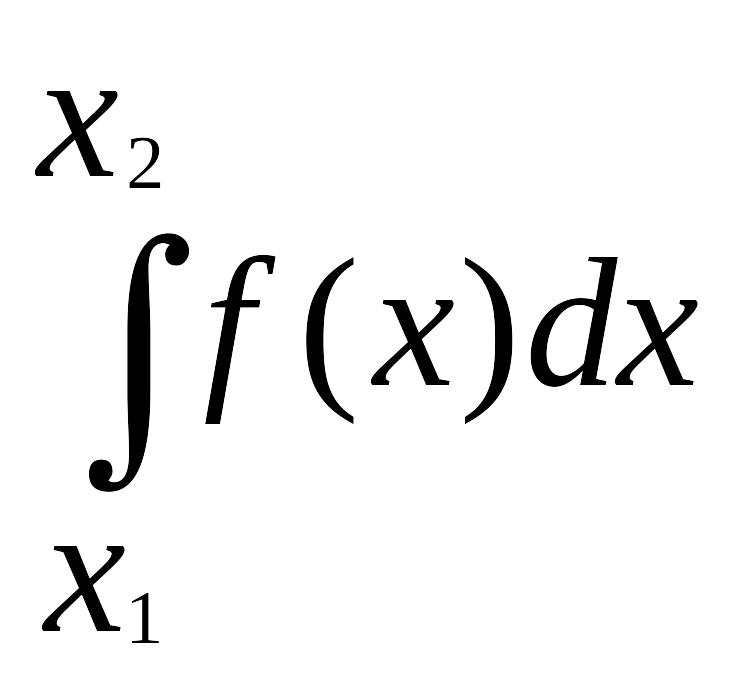₂) = . (2.2.2)

Доказательство. Р(x₁ X < x₂) = F(x₂) – F(x₁) = - =

= + = .

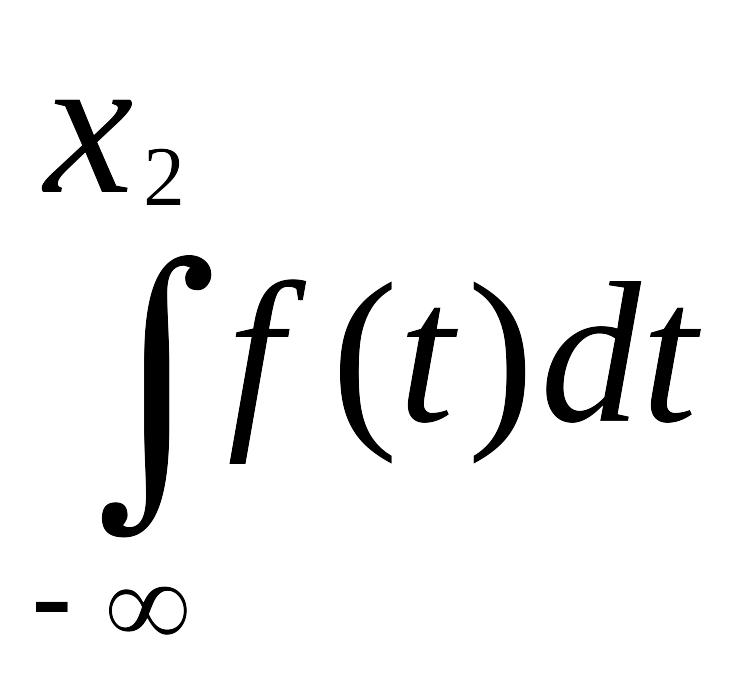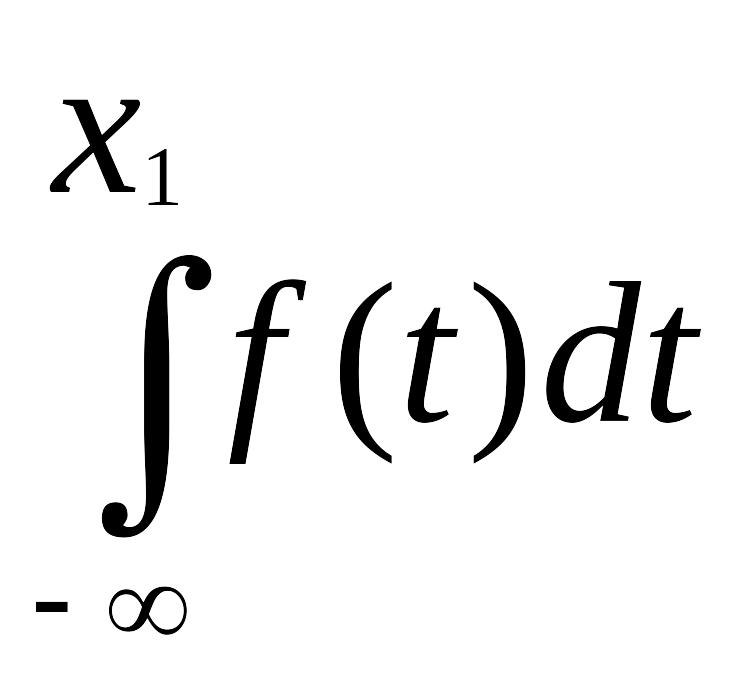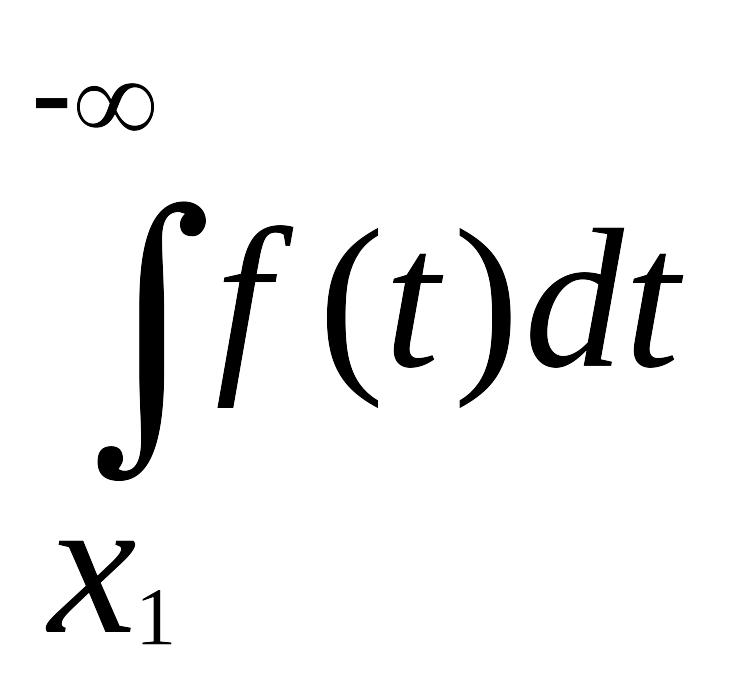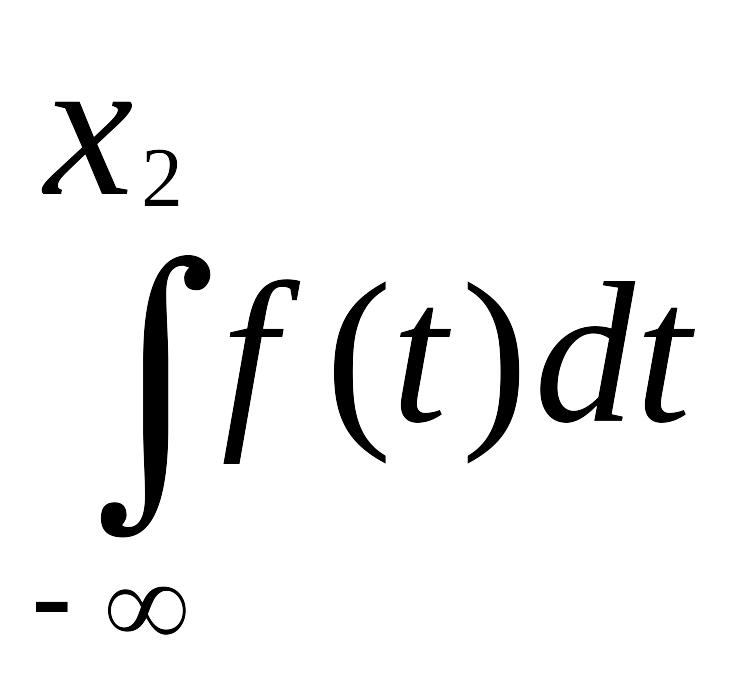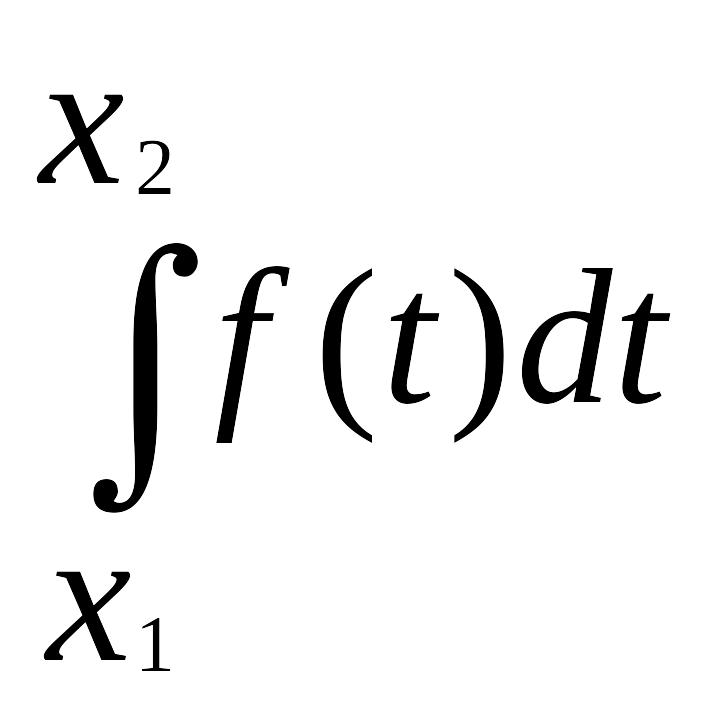Следствие 1. Р(x₁ X x₂) = Р(x₁ < X < x₂) = .

Здесь использовано свойство определенного интеграла, связанное с неизменностью его значения при добавлении (или исключении) любого конечного числа точек к промежутку интегрирования.

Следствие 2. Р(x < X < x + x) f(x)x. (2.2.3)

Равенство (2.2.3) выражает вероятностный смысл плотности вероятности и является следствием свойства 1.

Свойство 2. Р(Х = х) = 0. (2.2.4)

Доказательство следует из (2.2.3) при переходе к пределу при x  0.

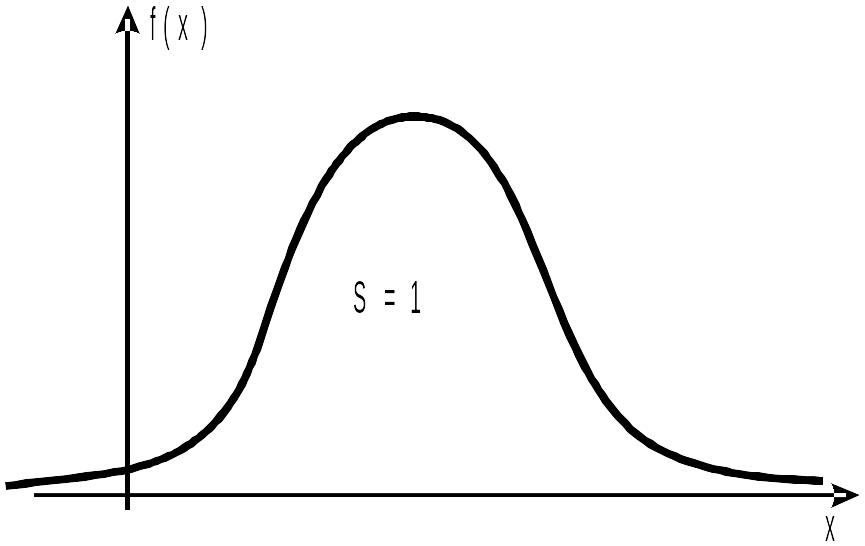
Свойство 3. (Условие нормировки) = 1 (2.2.5)

Д

Рис. 2.2.1

оказательство. F(x) =  , F(+ ) = = 1.

Замечание. Геометрически условие нормировки (2.2.5) выражает тот факт, что площадь криволинейной трапеции, расположенной под графиком плотности вероятности f(x), равна 1 (рис. 2.2.1).

Свойство 4. В точках x непрерывности f(x) выполняется равенство

F'(х) = f(x), (2.2.6)

т.е. F(x) является первообразной для f(x).

Доказательство следует из соответствующего свойства интеграла с переменным верхним пределом.

Примеры случайных величин непрерывного типа

1. Случайная величина, равномерно распределенная на отрезке [а, b]

С

Рис. 2.2.2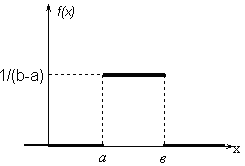

лучайная величина Х имеет равномерное распределение на отрезке [a, b], если ее плотность вероятности имеет вид

f(x) = .

Постоянную С можно определить из условия нормировки (2.2.5)

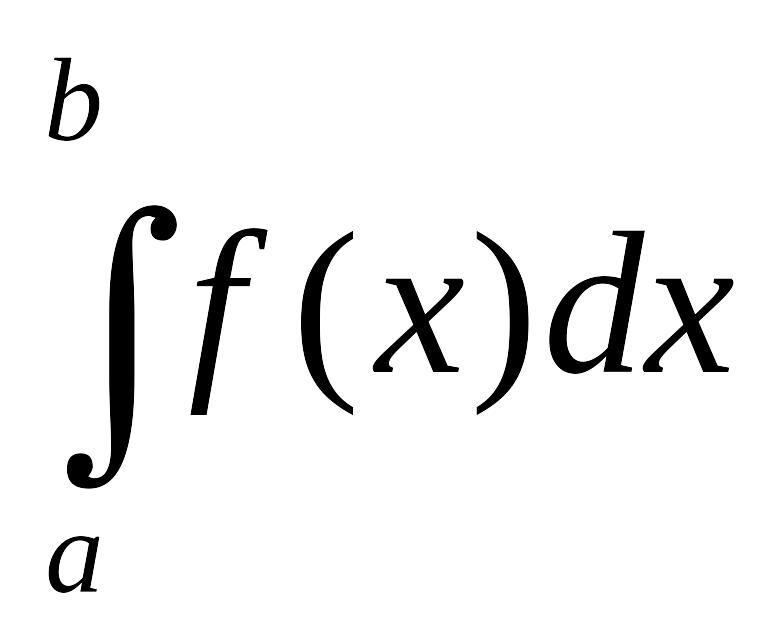= = С = С(b – a) = 1,

откуда С = 1/(b - a). Поэтому выражение для f(x) можно переписать в следующем виде:

f(x) = . (2.2.7)

График плотности вероятности равномерного распределения (2.2.7) представлен на рис. 2.2.2.

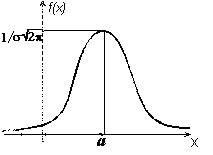
2. Случайная величина с нормальным законом распределения

Случайная величина Х называется распределенной по нормальному закону (закону Гаусса), если ее плотность вероятности имеет следующий вид:

, –∞ < x <∞, (2.2.8)

г

Рис. 2.2.3

де С(C > 0), а, ( > 0) – некоторые константы.

Замечание. Постоянную С в формуле для f(x) можно определить из условия нормировки – . Поэтому формулу для нормального распределения можно переписать в следующем виде:

f(x) = 1/( ) , –∞ < x <∞, (2.2.9)

Константы а,  называют параметрами нормального распределения. Поэтому нормальное распределение обозначают N(а,). График плотности вероятности нормального распределения показан на рис. 2.2.3.

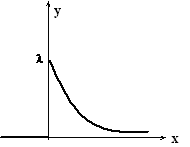
3. Случайная величина с показательным законом распределения

Случайная величина имеет показательное (экспоненциальное) распределение, если ее плотность вероятности имеет следующий вид:

f

Рис. 2.2.4

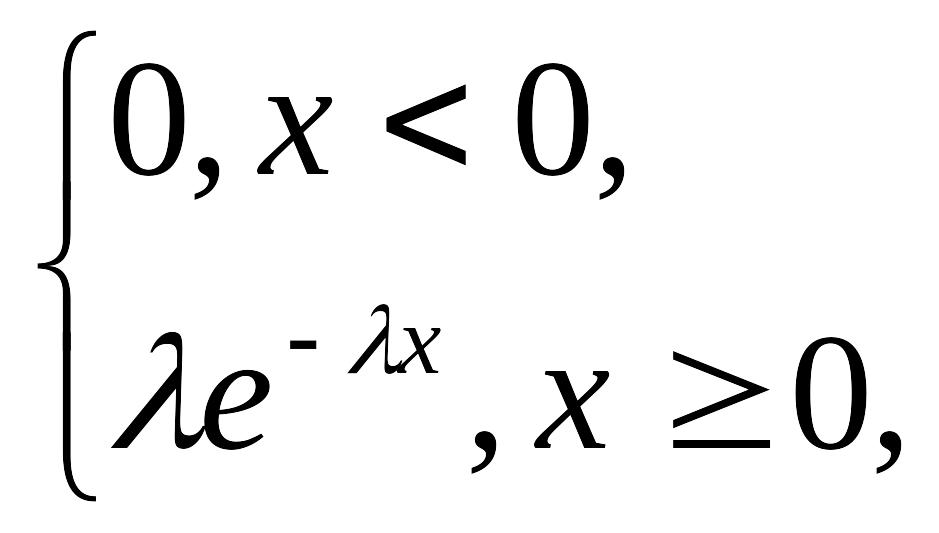= (2.2.10)

где – параметр показательного распределения. График f(x) представлен на рис. 2.2.4.

В приложениях теории вероятностей (например, теории массового обслуживания) случайная величина с показательным законом распределения часто выражает время безотказной работы системы или устройства.

Задача 2.2.1. Найти вероятность попадания случайной величины с нормальным законом распределения на заданный интервал ( ).

Решение. Плотность вероятности для случайной величины с нормальным законом распределения имеет вид f(x) = .

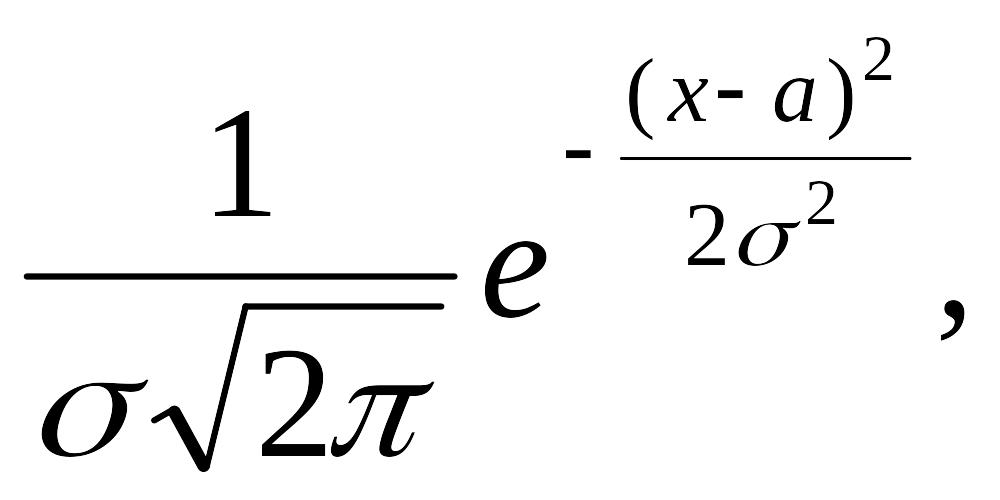
С учетом формулы (2.2.2) имеем

P = = = = = = = 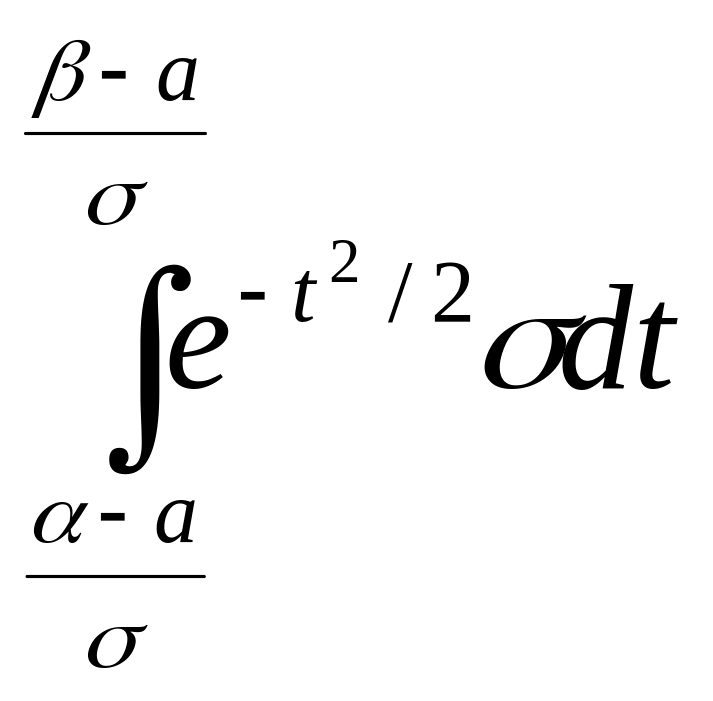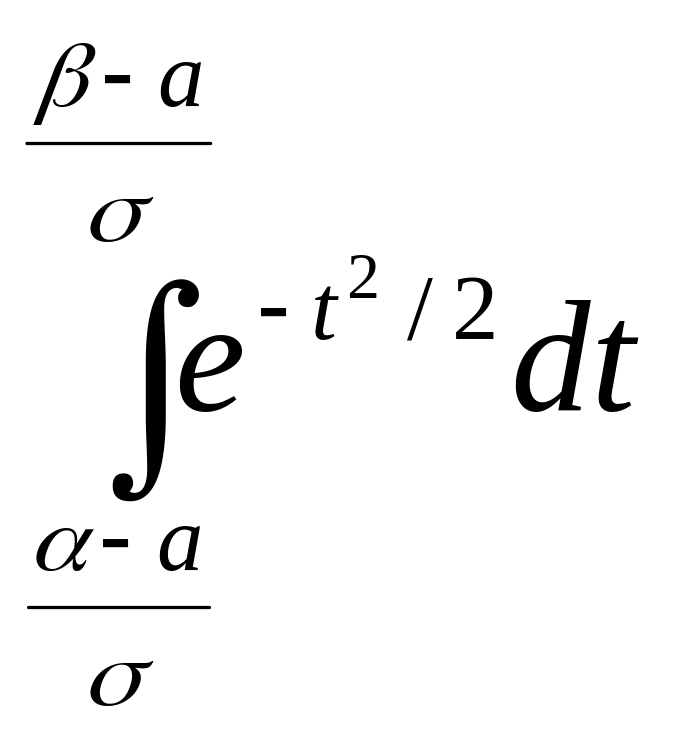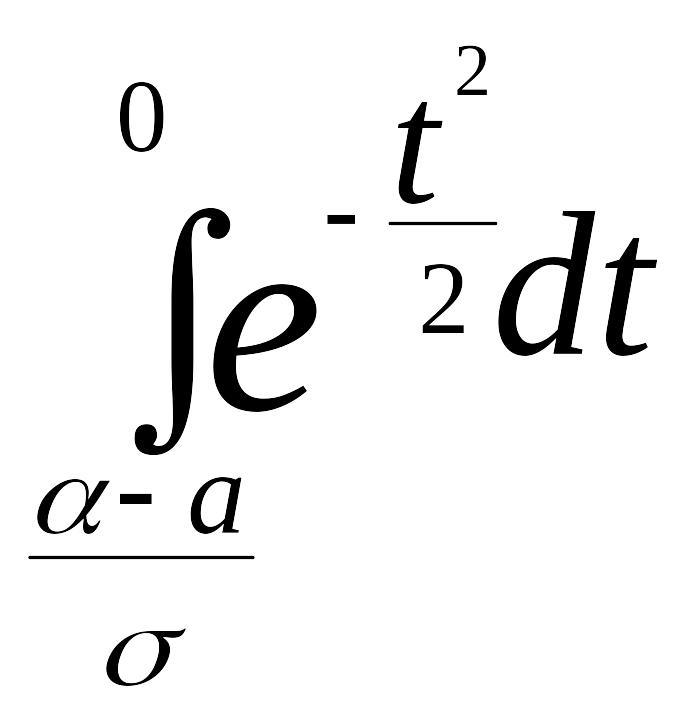+ 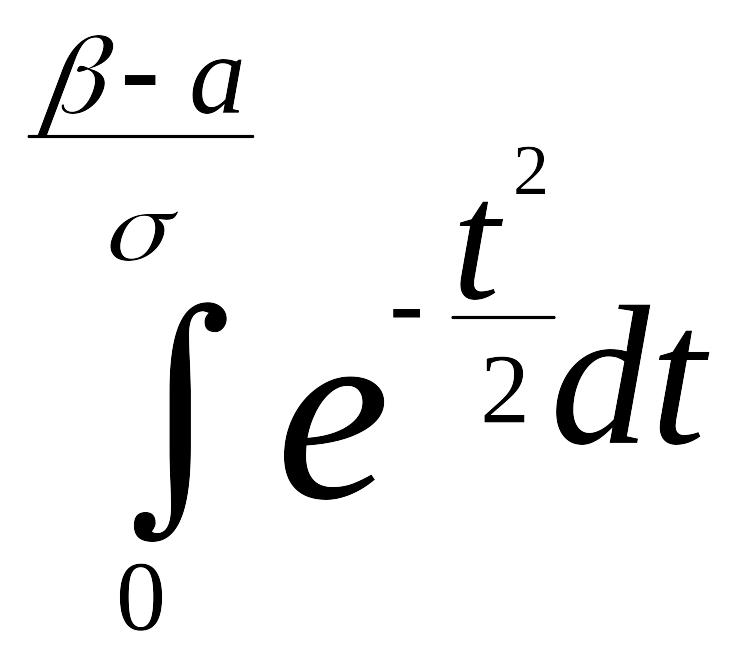= Ф - Ф .

Таким образом, P = Ф - Ф , (2.2.11)

где Ф(х) = — функция Лапласа, введенная ранее в подр. 1.8, значения которой определяются по табл. 4 приложения.

В частности, если требуется найти вероятность Р( ), имеем с помощью формулы (2.2.11)

Р( ) = Р( ) = Ф( ) - Ф( ) = Ф( ) - Ф(- ) = 2Ф( ).

Таким образом,

Р( ) = 2Ф( ). (2.2.12)