2. Случайные величины

2.1. Случайные величины. Случайные величины дискретного типа. Ряд распределения. Функция распределения

До сих пор мы имели дело со случайными событиями, которые являются качественной характеристикой опыта со случайным исходом. Количественной характеристикой его является случайная величина.

Случайной величиной будем называть переменную величину Х, которая в результате испытания принимает числовые (действительные) значения случайным образом, причем вероятности этих значений считаются известными.

Примеры. Число выпадений ''герба'' при n бросаниях; число попаданий в мишень при m выстрелах из орудия; число дефектных изделий в партии из k штук; число вызовов, поступающих на телефонную станцию в течение суток; ошибка при измерении дальности радиолокатором; рост при обследовании определенной совокупности людей; время безотказной работы телевизора; оценка на экзамене.

Случайные величины принято обозначать заглавными буквами латинского алфавита – X, Y, Z и т.д.

Более строгое определение случайной величины заключается в следующем.

Определение 2.1.1. Случайной величиной называется однозначная функция X(ω), определенная на Ω, для которой множество вида , т.е. является множеством, элементы которого являются случайными событиями для любого .

Определение 2.1.2. Случайная величина называется случайной величиной дискретного типа, если множество ее возможных значений является конечным или счетным множеством.

Простейшей формой закона распределения случайной величины дискретного типа является ряд распределения, представляющий собой таблицу, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:

Х	х1	х2	...	хn
P	p1	p2	...	pn

Здесь p_i = Р(Х = х_i), i = (вероятность того, что случайная величина Х принимает значение x_i). При этом p_i = 1.

Определение 2.1.3. Функцией распределения случайной величины Х называется функция, определенная на (-∞,∞) и определяемая равенством

F(x) = P(X < x). (2.1.1)

Задача 2.1.1. Построить ряд распределения, а также функцию распределения числа выпадений ''герба'' при трех бросаниях ''правильной'' монеты.

Решение. В этой задаче Х – число выпадений ''герба'' при трех бросаниях монеты. Значения, которые может принимать эта случайная величина Х – 0, 1, 2, 3. Вероятности этих значений вычисляются по формуле Бернулли: Р₃(0) = (1/2)⁰(1/2)³ = 1/8; Р₃(1) = (1/2) (1/2)² = 3/8; Р₃(2) = (1/2)² (1/2) = 3/8; Р₃(3) = (1/2)³ (1/2)⁰ = 1/8.

Ряд распределения этой случайной величины имеет вид

Х	0	1	2	3	.
Р	1/8	3/8	3/8	1/8

На основе определения 2.1.3 и ряда распределения можем найти функцию распределения:

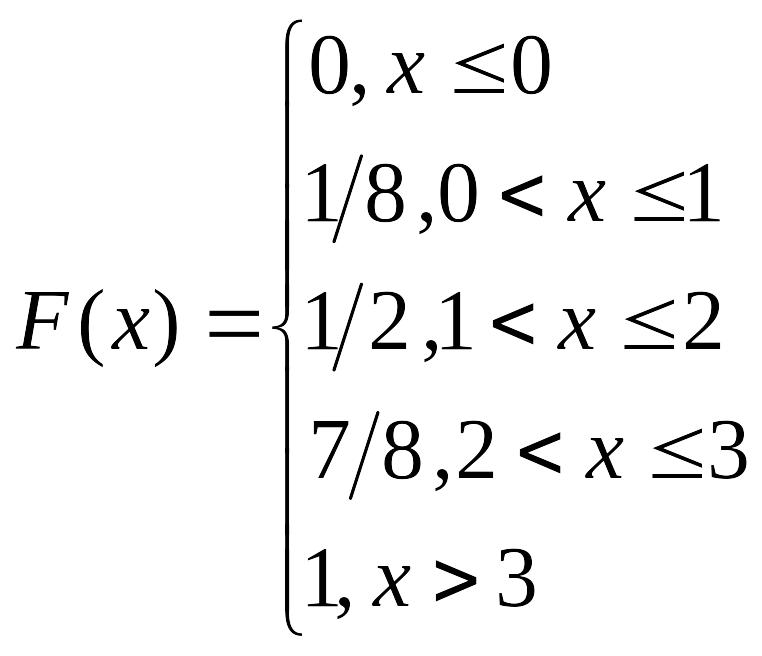
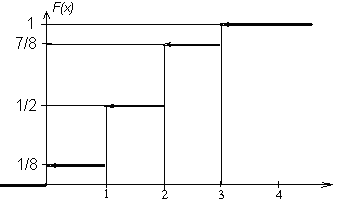
График функции F(x) представлен на рис. 2.1.1.

x

Рис. 2.1.1

Примеры случайных величин дискретного типа

1. Случайная величина биномиального типа

В схеме независимых испытаний Бернулли случайной величиной является Х – число ''успехов'' в n независимых испытаниях; она и называется случайной величиной с биномиальным законом распределения. Значения, которые может принимать эта случайная величина – 0, 1, 2, ..., n; вероятности этих значений вычисляются по формуле Бернулли:

.

Ряд распределения этой случайной величины имеет вид

Х	0	1	2	3	...	n	.
Р	Pn(0)	Pn(1)	Pn(2)	Pn(3)	...	Pn(n)

2. Случайная величина с геометрическим законом распределения

Случайной величиной с геометрическим законом распределения называется Х – число испытаний до первого ''успеха'' в схеме независимых испытаний Бернулли. Ряд распределения этой случайной величины имеет вид

X	1	2	3	...	k	...	.
Р	р	qp	q2p	...	qk-1p	...

3. Случайная величина, распределенная по закону Пуассона

Случайной величиной, распределенной по закону Пуассона, называется случайная величина Х, принимающая любые целые неотрицательные значения, вероятности которых вычисляются по формуле Пуассона:

Р(k) = , k = 0, 1, 2, ... .

Здесь – параметр этого распределения. Известно, что случайная величина, распределенная по закону Пуассона, является предельным случаем биномиального распределения при n и p 0 (np = ).

Ряд распределения этой случайной величины имеет вид

Х	0	1	2	...	K	...	.
P				...		...

Свойства функции распределения случайной величины

Свойство 1. Функция распределения является неубывающей функцией на (‑ , ).

Доказательство. Требуется доказать, что для .

В

Рис. 2.1.2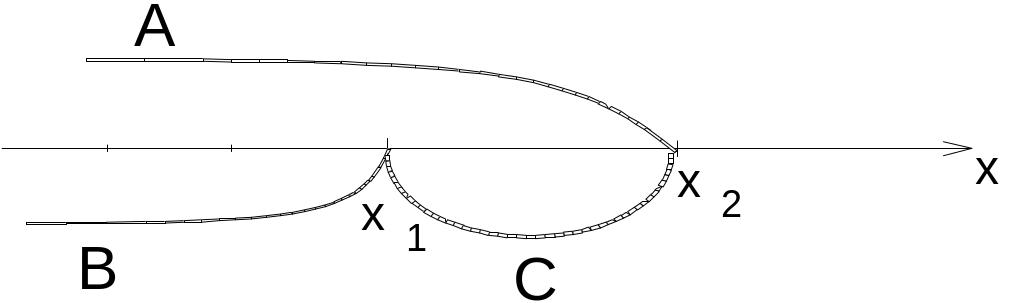

ведем следующие случайные события: А = {X < x₂}, В = {X < x₁}, C={x₁  X < x₂}.

Запись А = {X < x₂} обозначает случайное событие, заключающееся в том, что случайная величина Х принимает значения, меньшие х₂; аналогично раскрываются случайные события В и С. Тогда, очевидно, А = В + С, и по теореме сложения для несовместных событий имеем:

Р(А) = Р(В + С) = Р(В) + Р(С), Р(Х < х₁) = Р(Х < х₁) + + Р(x₁  X < x₂), откуда имеем

F(x₂)=F(x₁) + P(x₁ X < x₂). (2.1.5)

Из (2.1.5) очевидно, что F(x₁) F(x₂).

Свойство 2. Р(x₁ X < x₂) = F(x₂) - F(x₁).

Доказательство. Следует из равенства (2.1.5).

Свойство 3. Функция распределения F(x) случайной величины непрерывна слева в х  (– , ), т.е. F(x – 0) = F(x).

Свойство 4. Для х (-∞,∞) Р(Х  x) = F(х + 0).

Свойство 5. Р(x₁  X  x₂) = F(х₂ + 0) – F(x₁).

Доказательство. Аналогично доказательству свойства 1 введем случайные события: А = {X  x₂}, В = {X < x₁}, C= {x₁  X  x₂}. Тогда имеем

Р(А) = Р(В) + Р(С), или Р(Х  х₂) = Р(Х < х₁) + Р(x₁  X  x₂),

но Р(Х  x₂) = F(x₂ + 0), Р(Х < х₁) = F(x₁), и тогда Р(x₁  X  x₂) = F(x₂ + 0) – F(x₁). Свойство 6. F(–∞) = 0, F(+∞) = 1.

Здесь под символами F(- ) и F(+ ) понимаем следующие пределы: , .

Доказательство очевидно, если заметить, что F(–∞) = P(X < –∞) = 0;

F(+∞) = P(X < ∞) = 1.