1.8. Схема независимых испытаний Бернулли. Формула Бернулли. Формула Пуассона. Локальная и интегральная теоремы Муавра-Лапласа

Пусть имеем серию n независимых испытаний, в каждом из которых некоторое случайное событие А наступает с одной и той же вероятностью p = P(A), не изменяющейся от испытания к испытанию. Само событие А условно называется “успехом” (обозначается впредь У в отличие от “неуспеха”, обозначаемого H), а последовательность n независимых испытаний с двумя исходами У и H называется последовательностью независимых испытаний Бернулли.

Найдем вероятность того, что в серии из n испытаний Бернулли "успех" (У) наступит ровно k раз. В этом случае любой исход n испытаний Бернулли представляет собой последовательность длины n, состоящую из k "успехов" (У) и (n – k) "неуспехов" (Н). Вероятность каждого такого исхода по теореме умножения независимых случайных событий равна p^k(l - p)^n-k или p^kq^n-k, где q=1 - p. Число таких комбинаций равно числу способов выбора k мест из n для "успеха", т.е. .

Таким образом, вероятность того, что в серии из n испытаний Бернулли "успех" наступит ровно k раз, равна

P_n(k)= p^kq^n-k. (1.8.1)

Формула (1.8.1) называется формулой Бернулли. Сравнивая формулы (1.8.1) и (1.3.9), видим, что правая часть формулы Бернулли равна общему члену разложения бинома Ньютона

.

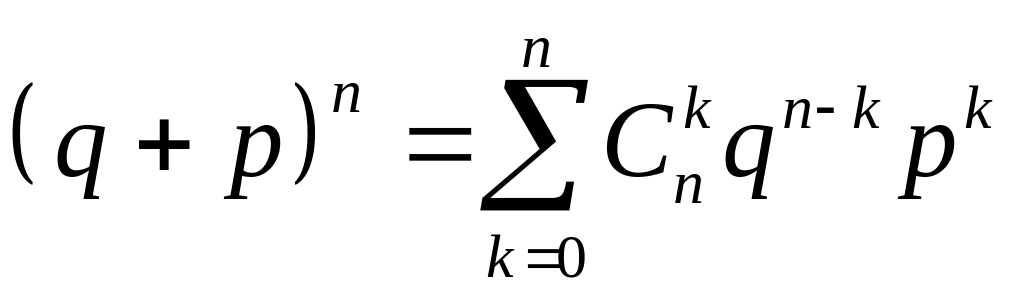Рассмотрим частные случаи формулы Бернулли.

1. Вероятность того, что в n испытаниях "успех" наступит n раз, равна

.

2. Вероятность того, что в n испытаниях Бернулли "успех" вообще не наступит, равна

.

3. Вероятность того, что в n испытаниях Бернулли "успех" наступит не более чем m раз, равна

P(k m) = P_n(0) + P_n(l) + ... + P_n(m)=

4. Вероятность того, что "успех" наступит в n испытаниях не менее m раз, равна

P(k m) = P_n(m) + P_n(m-l)+... + P_n(n) = (1.8.2)

Задача 1.8.1. Найти вероятность того, что в семье, имеющей 5 детей будет: 1) 2 мальчика; 2) не менее двух мальчиков. Считать, что вероятности рождения мальчиков и девочек одинаковы и равны 0,5.

Решение.

1. Считая "успехом" рождение мальчика с p=0,5 (q = 0,5), имеем по формуле Бернулли (1.8.1): Р₅(2)= 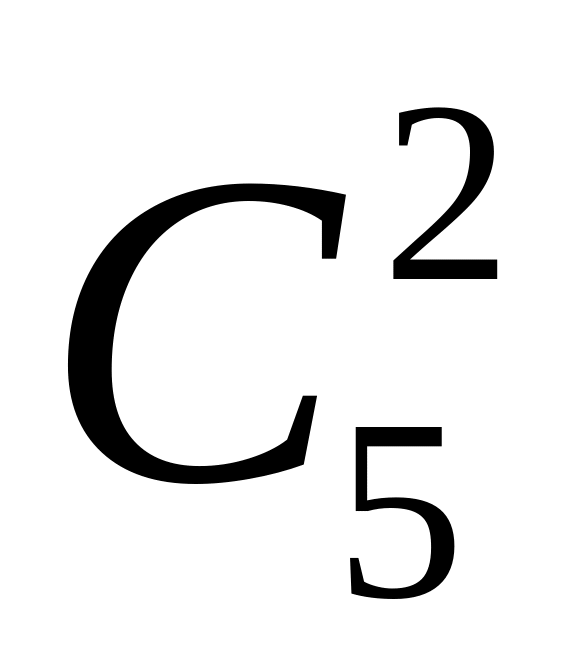(1/2)²(1/2)³= 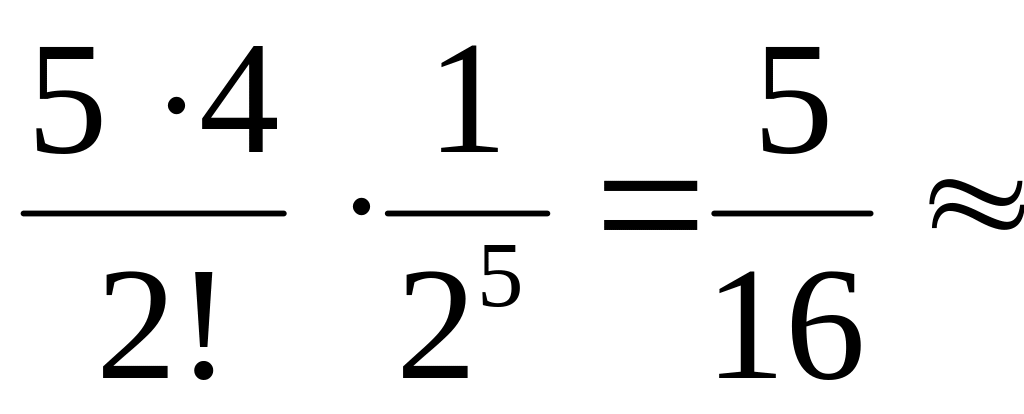0,31.

2. Используя формулу (1.8.2) c n = 5, m =2, имеем

P₅(k 2) = Р₅(2) + Р₅(3) + Р₅(4) + Р₅(5) =

= (1/2)²(1/2)³+ (1/2)³(1/2)² + (l/2)4(1/2) + (l/2)⁵ ≈ 0,81.

Задача 1.8.2. Что вероятнее: выиграть у равносильного противника в шахматы 2 партии из трех или 3 партии из четырех?

Решение. Считая "успехом" выигрыш у равносильного противника с p = 1/2, найдем вероятности по формуле Бернулли(1.8.1):

Р₃(2)= (1/2)²(1/2) = 3/8, Р₄(3) = (1/2)³(1/2) = 1/4.

Вероятнее выиграть 2 партии из трех.

Наивероятнейшим числом наступлений события А (успеха) в n независимых испытаниях Бернулли называется число, для которого вероятность P_n(m₀) не меньше вероятности любого из остальных возможных исходов испытаний. Пусть m₀ — наивероятнейшее число наступлений события А в n испытаниях Бернулли; тогда по определению Р_n(m₀) P_n(m₀ + 1) и P_n(m₀) Ρ_n(m₀ - 1).

Раскрывая эти соотношения с помощью формулы (1.8.1), получим неравенство для определения m₀:

nр - q m₀ nр + р. (1.8.З)

Схема выборочного контроля

Пусть покупатель готов принять партию товара грейпфрутов лишь в том случае, если менее 2% фруктов не удовлетворяют стандарту. Пусть, кроме того, он считает, что нестандартные плоды встречаются случайно. (Это может оказаться неверным для дефектов, вызванных, например, грибковыми заболеваниями, которые распространяются от одного плода на соседние. Однако предположение о случайности обоснованно, если дефекты возникают вследствие механического повреждения, порчи кожуры, высыхания плода и т. д.).

Покупатель не в состоянии проверить все фрукты в тысячах ящиков, а если бы он этим и занялся, за время проверки число испорченных плодов наверняка стало бы больше, чем было вначале.

Если предложить покупателю выбрать сотню фруктов, и если он найдет лишь один испорченный плод или не найдет ни одного, можно ли считать, что содержание дефектных плодов в партии не превосходит 2%?

Рассмотрим гипотезу, что во всей партии ровно 2% дефектных плодов. Какова вероятность того, что в случайной выборке из 100 плодов мы обнаружим 0 или 1 дефектный плод? В очень большой партии, содержащей тысячи грейпфрутов, после сравнительно небольшой выборки доля нестандартных плодов изменится незначительно. Поэтому вероятность появления в выборке 0 или 1 дефектного плода можно подсчитать по формуле Бернулли: первая равна 0,98¹⁰⁰ 0,133; вторая – 0,270. Поэтому искомая вероятность равна p = 0,133 + 0,270 = 0,403, т.е. вероятность того, что партия будет принята, равна 40%. С другой стороны, если бы все плоды в выборке были стандартны, партия определенно будет принята, с вероятностью 1 или 100% (ведь в выборке нет дефектных фруктов); если же все плоды в выборке нестандартны, такая партия будет отвергнута.

При 5-процентном содержании нестандартных плодов вероятность выборки, содержащей не более одного испорченного фрукта, составляет всего 0,037 или 3,7%.

Как отнесется к этому методу выборочного контроля оптовый поставщик и его клиенты? Шансы для действительно качественной партии грейпфрутов быть принятой составляет всего 40% и в то же время существует вероятность 3,7%, что будет принята партия с 5% нестандартных плодов.

При большом числе n повторных испытаний использование формулы Бернулли (1.8.1) затруднительно в связи с необходимостью выполнения действий над большими и малыми числами. Например, при n = 50, k = 20, p = 0,1, q = 0,9 , 50!=30414093·10⁵⁷; 30!=2652286·10²⁵; 20!=24329020·10¹¹.

Поэтому возникает необходимость в асимптотических формулах, позволяющих с достаточной степенью точности определить эти вероятности. Впервые такая формула была найдена А. Муавром для частного случая p=q=1/2, а затем обобщена П. Лапласом на случай произвольного p, отличного от 0 и 1. Этот результат носит название локальной теоремы Муавра-Лапласа.

Локальная теорема Муавра-Лапласа. Пусть вероятность "успеха" р в каждом из n испытаний Бернулли постоянна и отлична от 0 и 1. Тогда имеет место следующая приближенная формула (которая тем точнее, чем больше n):

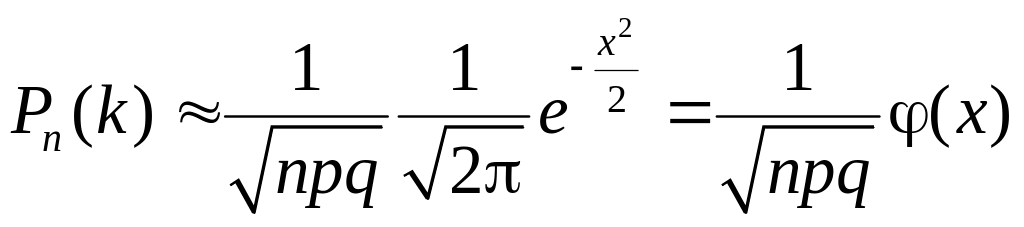, (1.8.4)

где , .

Функция , очевидно, является четной и ее значения для положительных значений x приведены в табл.3 приложения.

Задача 1.8.3. Вероятность успеха в каждом испытании равна 1/4. Какова вероятность того, что при 300 испытаниях успех наступит ровно 85 раз?

Решение. Используя формулу (1.8.4), имеем

0,1647;

Следует заметить, что формула (1.8.4) непригодна (дает слишком большую погрешность), если вероятность события мала (р 0,1). При больших n и малых p используют асимптотическую формулу Пуассона

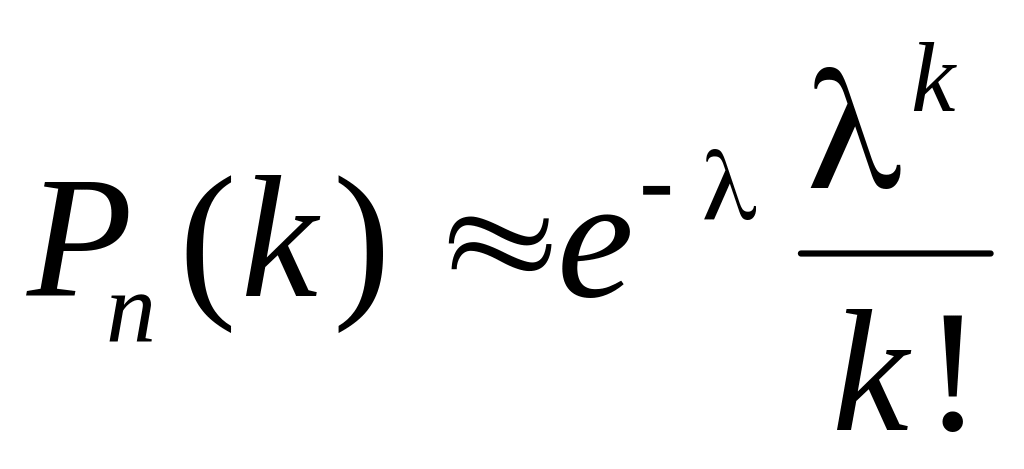, (1.8.5)

где λ =np.

В приближенной формуле (1.8.5) параметры n и р объединены в один параметр λ = np; n должно быть не менее нескольких десятков, а лучше сотен, а значение параметра λ = np должно находиться между 0 и 10. При больших λ рекомендуется применять локальную теорему Лапласа.

Закон Пуассона (1.8.5) находит применение в следующих типовых задачах.

Задача о распределении случайных точек в области D

Пусть в области D с площадью S размещаются n точек, причем события, заключающиеся в попадании случайной точки в любую заранее заданную ее часть Δ постоянной (например, единичной) площади, равновероятны. Если λ = n/S – среднее число точек, попадающих в Δ, то при больших n и S (p = 1/S мало) вероятность того, что в заданную область Δ попадает ровно k точек, вычисляют приближенно по формуле Пуассона.

Задача о вызовах на АТС. Пусть n – число вызовов абонентов, поступающих за время t на АТС. Если λ = n/t – среднее число вызовов, поступающих на АТС за единицу времени (например, за 1 минуту), то вероятность того, что за единицу времени поступит k вызовов, также можно вычислить по формуле Пуассона (1.8.5).

Задача 1.8.4. АТС получает в среднем за 1 час 300 вызовов. Какова вероятность того, что за минуту она получит ровно 2 вызова?

Решение. За минуту АТС получает в среднем 300/60 = 5 вызовов, т.е. λ =5. Искомую вероятность найдем по формуле Пуассона (1.8.5):

Страхование. Рассмотрим случайную величину X - число требований в течение времени t. Эта случайная величина считается распределенной по закону Пуассона, и вероятность того, что за время t появятся точно k требований, вычисляется по формуле

.

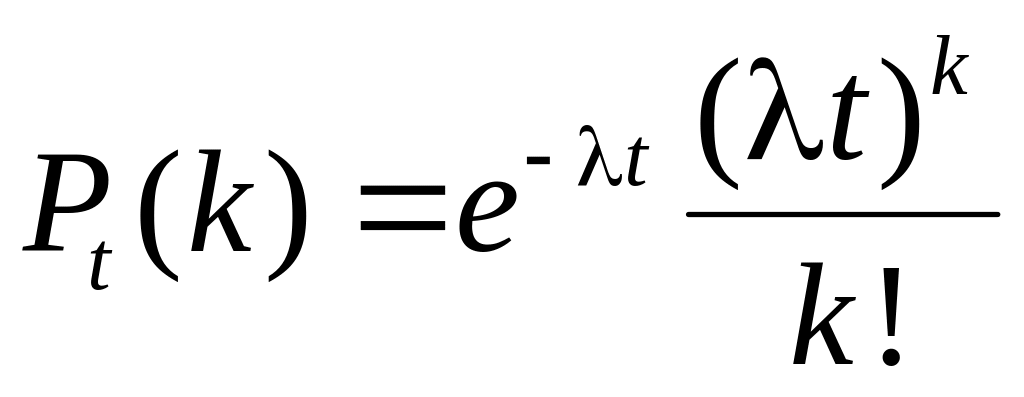Здесь λ – ожидаемое (среднее) число требований в единицу времени (например, за 1 день). Тогда вероятность того, что в течение года появится ровно k требований равно

.

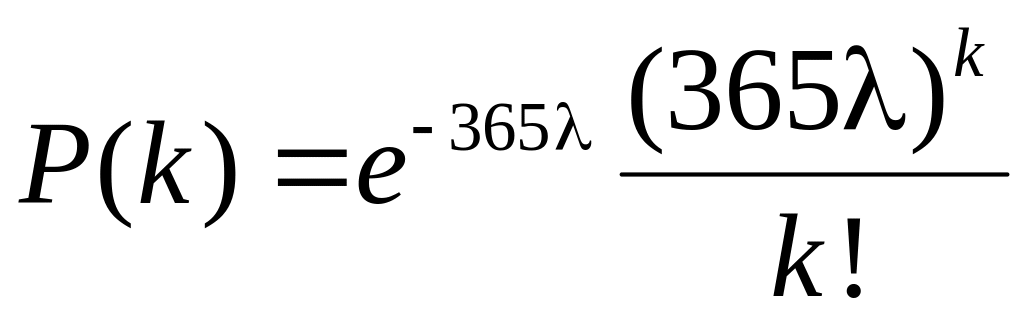Здесь 365λ – ожидаемое (среднее) число требований в год.

Однако практически при большом числе испытаний n и не слишком малой вероятности p нас редко интересует вероятность того, что "успех" наступит точно m раз; наиболее важно оценить вероятность того, что число "успехов" лежит в некотором интервале. Такую вероятность можно оценить с помощью интегральной теоремы Муавра-Лапласа.

Интегральная теорема Муавра-Лапласа. Пусть m – число "успехов" в серии из n независимых испытаний, p – вероятность "успеха" в каждом испытании, 0<р<1, ,b R, <b. Тогда

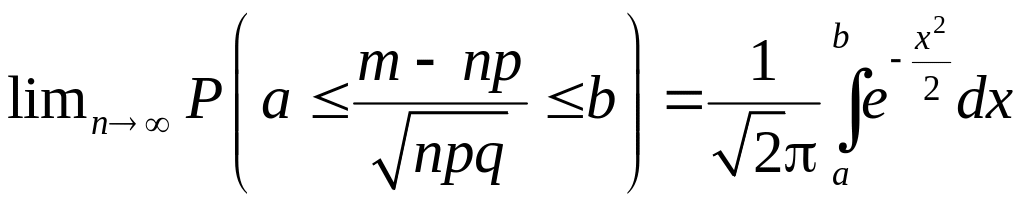, (1.8.6)

причем стремление к пределу равномерно относительно a и b, ‑∞ <   < b < +∞.

Практическое применение интегральной теоремы Муавра-Лапласа основано на приближенной формуле

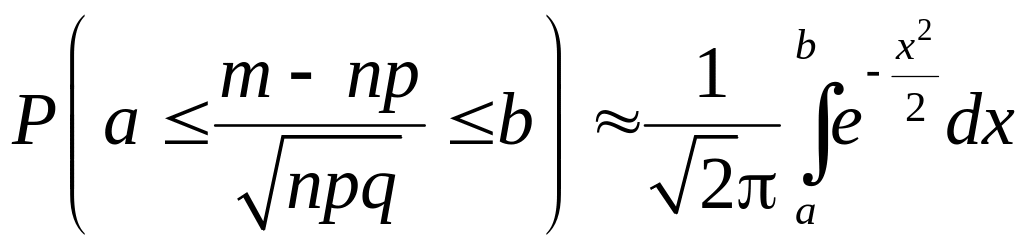. (1.8.7)

Формула (1.8.7) обеспечивает хорошую точность уже при значениях npq10.

Рассмотрим типичные задачи, связанные с интегральной теоремой Муавра-Лапласа.

1. В серии из n испытаний с вероятностью успеха в каждом испытании р требуется найти вероятность того, что число успехов будет заключено между заданными числами α и β, 0α<βn. Имеем

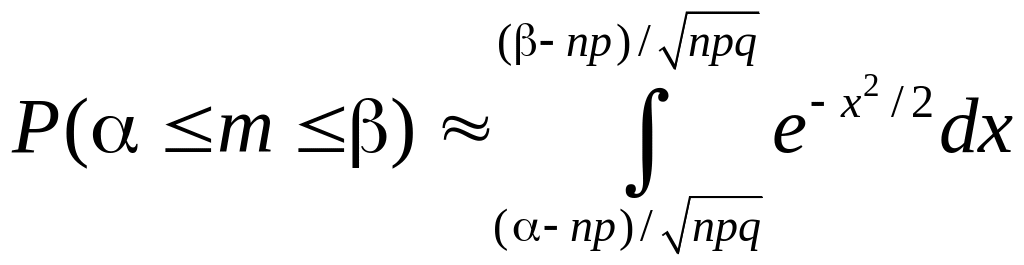. (1.8.8)

Введем функцию

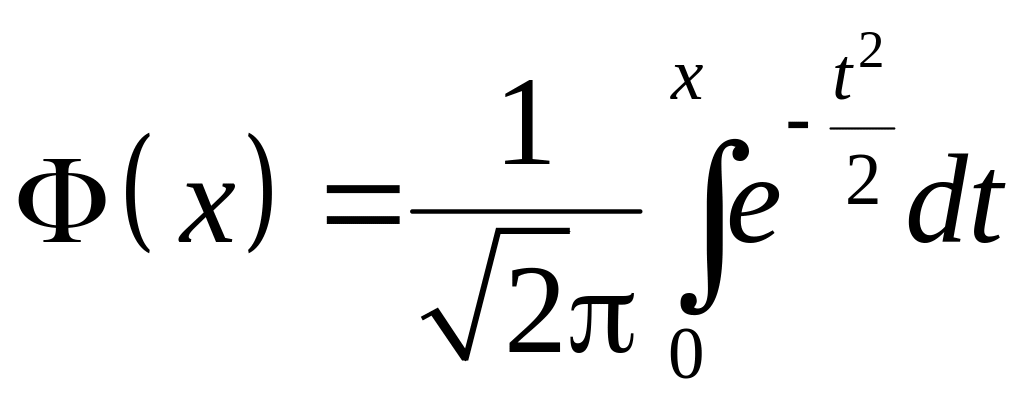, (1.8.9)

называемую интегралом Лапласа (интегралом вероятности). Эта функция обладает следующими свойствами: 1) Ф(х) является возрастающей функцией на промежутке (‑∞, +∞); 2) Ф(х) – нечетная функция; 3) Ф(0) = 0; Ф(-∞) = -1/2; Ф(∞) = 1/2. Функция Ф(х) довольно быстро стремится к 1/2 при х→∞, например, Ф(3)≈0,499. Значения Ф(х) заданы в табл. 4 приложения. Поэтому формула (1.8.8) может быть переписана в следующем виде:

. (1.8.10)

Задача 1.8.5. Какова вероятность того, что при 100 бросаниях правильной монеты герб появится от 40 до 60 раз?

Решение. Используя формулу (1.8.10), имеем Ф(2) – Ф(–2) = 2Ф(2) ≈ 2∙0,4772 = 0,9544 (значение Ф(2) вычислено по табл.4).

2. В схеме независимых испытаний Бернулли требуется оценить вероятность того, что частота m/n появлений успеха в n испытаниях (при больших n) отклоняется от вероятности p по модулю не больше, чем на ε .

. (1.8.11)

Если же требуется определить, какое наименьшее число испытаний надо произвести, для того чтобы с вероятностью, не меньшей β, частота m/n появлений успеха отклонялась от вероятности ρ по модулю не больше, чем на ε, требуемое n определяем, решив неравенство

.

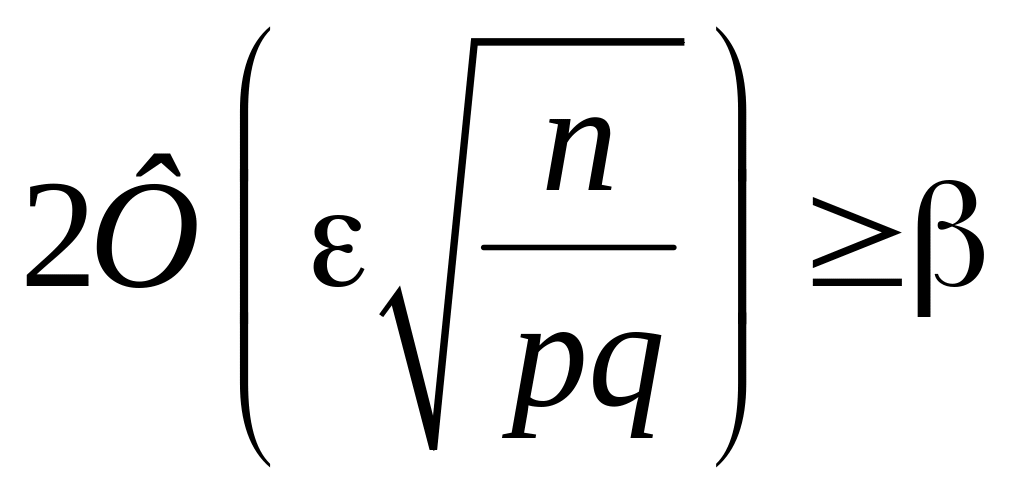Задача 1.8.6. Найти вероятность того, что частота m/n появлений герба в серии из 100 бросаний "правильной" монеты отклоняется от вероятности р=1/2 по модулю не более чем на 0,01.

Решение. Используя формулу (1.8.11), имеем

.