1.6. Формула полной вероятности и формула Байеса

Пусть событие А может произойти с одним и только с одним из событий В₁,В₁,...,В_n (называемых впредь гипотезами), которые образуют полную группу попарно несовместных событий. Пусть даны вероятности этих гипотез Р(В₁),...,Р(В_n), а также условные вероятности события А при условиях этих гипотез Р(А/В₁),..., Р(А/В_n). Требуется определить Р(А).

Имеем очевидное равенство Α = Α·Β₁+Α·Β₂+…+А·В_n.

Применяя последовательно аксиому сложения для несовместных событий, а затем теорему умножения для каждого слагаемого суммы, имеем

Р(А) = Р(В₁)· Р(A/В₁)+...+P(B_n)· Р(А/В_n) (1.6.1)

или

P(A)=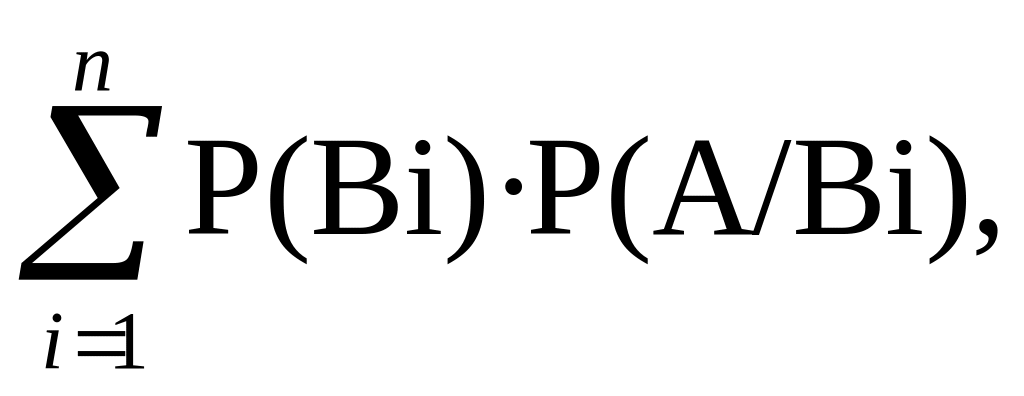

которая называется формулой полной вероятности.

Задача 1.6.1. Имеются 2 урны, в каждой из которых находится по 10 шаров, причем в 1-й урне 7 белых и 3 черных шара, во 2-й – 2 белых и 8 черных. Некто подходит наудачу к одной из урн и вынимает шар. Найти вероятность того, что вынут белый шар.

Решение. Пусть А – вытягивание белого шара. Введем гипотезы, при которых может произойти событие А: B₁ – подход к 1-й урне, В₂ – подход ко 2-й урне. Тогда Р(А) можно вычислить по формуле полной вероятности

Р(А) = Р(В₁) Р(А/В₁) + Р(В₂) P(A/В₂);

имеем

Р(А)= .

Задача 1.6.2. На экзамене 30 билетов, из которых для студента 25 "счастливых", которые он знает. Каким более выгодно брать ему билет: первым или вторым?

Решение. Пусть А - вытягивание счастливого билета. Если студент X берет билет первым, то Р(А)= . Если студент Х берет билет вторым (после студента Y), то Р(А) зависит от гипотез В₁ и В₂: В₁ - Υ вытянул "счастливый" для X билет; В₂- Υ вытянул "несчастливый" для X билет. Тогда

Ρ(Α) = Ρ(Β₁)Ρ(Α/Β₁) + Ρ(Β₂)Ρ(Α/Β₂)

и

P(А) = .

Вывод: вероятность для X вытянуть "счастливый" билет не зависит от того, каким он будет брать билет – первым или вторым.

Пусть теперь при прежних условиях относительно случайных событий А и гипотез В₁, В₂, …, В_n известен результат опыта, т. е. известно, что событие А произошло. Требуется найти так называемые апостериорные (послеопытные) вероятности Р(В_i/A), i=l, 2, ..., n - вероятности гипотез после опыта. Используя теорему умножения вероятностей, имеем P(AB_i) = Р(B_i)P(А/B_i) = = P(A)P(B_i/A).

Из последнего равенства получим формулу Байеса

, i=1, 2, …, n, (1.6.2)

где Р(А) вычисляется предварительно по формуле полной вероятности (1.6.2).

Задача 1.6.3. При составе двух урн из задачи 1.6.1 некто подходит наудачу к одной из урн и вынимает шар. Он оказался белым. Найти вероятность того, что он вытянут из 2-й урны.

Решение. Пусть как и прежде А – вытягивание белого шара из урны, В₁ – подход к 1-й урне, В₂ – подход ко 2-й урне. Требуется найти Р(В₂/А). По формуле Байеса (1.6.2) имеем

_,

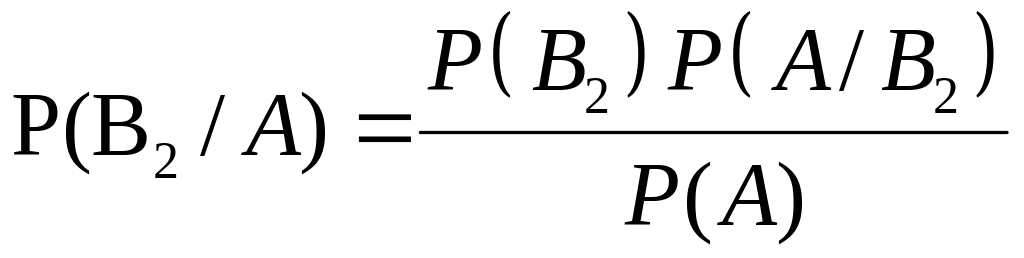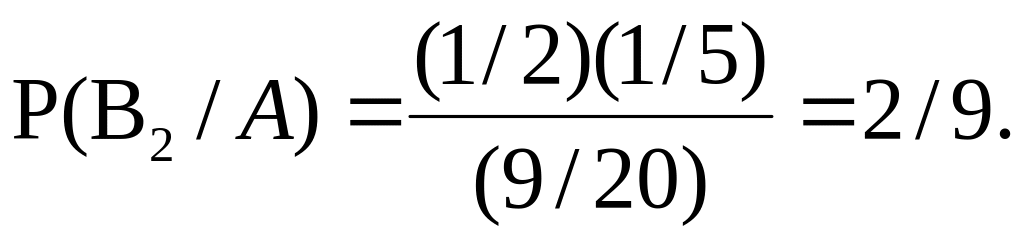
1.7. Геометрические вероятности

В некоторых случаях пространство элементарных событий  содержит несчетное множество исходов. В этом случае аксиоматическое определение вероятности случайного события представляет определенные сложности, главным образом, в части ее счетной аддитивности.

Этот недостаток можно преодолеть, используя геометрическое определение вероятности, находя вероятность попадания точки в некоторую область, имеющую меру (длину – для отрезка; площадь для области на плоскости; объем для области в пространстве). Например, если поставлена задача о вероятности попадания точки в некоторую область A, являющуюся частью области попадания , при условии, что эта вероятность не зависит от положения области A в области , а зависит лишь от меры области A, то эту вероятность можно определить по следующей формуле:

Р(А)=m(A)/m(). (1.7.1)

Рассмотрим следующую классическую задачу.

Задача о встрече. Два лица договорились о встрече в течение времени Т. Любой из пришедших первым ждет в течение времени t Т, после чего уходит. Найти вероятность того, что встреча состоится.

Решение. Обозначим моменты прихода первого и второго лица через x и y соответственно, причем 0 х, у Т.

Встреча состоится, если выполнится неравенство |у–х| t, которое можно переписать в виде х–t у х+t. Представим соответствующие области А и  на координатной плоскости (рис. 1.7.1).

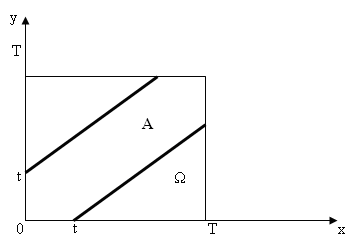
Рис. 1.7.1

Используя геометрическое определение вероятности попадания точки внутрь области А, определяющую вероятность встречи, имеем

.
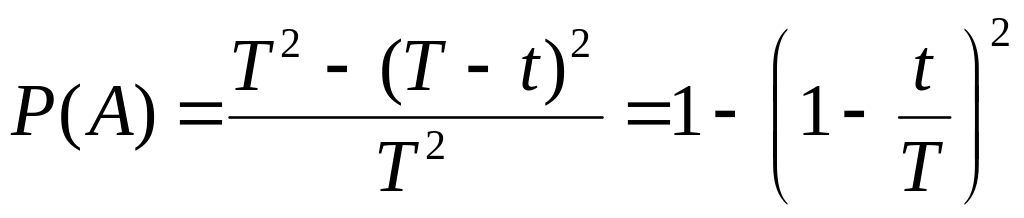