Вариант 7
Задача 1. Два автомата производят детали, которые поступают на общий конвейер. Производительность первого автомата вдвое меньше второго. Вероятность изготовить бракованную деталь на первом автомате равна 0,06, на втором 0,09. Взятая наудачу деталь оказалась стандартной. Какова вероятность того, что она изготовлена первым автоматом
Задача 2. Подбрасываются две игральные кости. Составить закон распределения суммы очков и вычислить числовые характеристики этого распределения.
Задача 3. Вероятность рождения мальчика 0,515. Чему равна вероятность того, что среди 80 новорожденных 42 мальчика
Задача 4. Случайная величина Х задана функцией распределения F (x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.
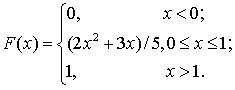
Задача 5. Известны математическое ожидание а и среднее квадратическое отклонение нормально распределенной случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (,); а=6, =2, =3, =10.
Задача 6. Дисперсия случайной величины Х равна 4. Сколько требуется произвести независимых опытов, чтобы с вероятностью не менее 0,9 можно было ожидать, что среднее арифметическое значение этой случайной величины будет отличаться от ее математического ожидания менее чем на 0,5
Задача 7. Дана двумерная случайная величина (X, Y). Найти ее корреляционную матрицу.
-
X\Y
- 2
3
-1
0,05
0,1
1
0,25
0,15
2
0,15
0,3
Вариант 8
Задача 1. Из 1000 ламп 640 и 80 принадлежат соответственно первой и второй партиям, остальные – из третьей партии. В первой партии обнаружено 6 бракованных ламп, во второй – 5, в третьей – 4. Наудачу выбирают одну лампу. Определить вероятность того, что выбранная лампа годная.
Задача 2. На пути движения автомобиля четыре светофора. Каждый из них с вероятностью 0,5 либо разрешает, либо запрещает автомобилю дальнейшее движение. Составить закон распределения числа светофоров, пройденных автомобилем до первой остановки, а также математическое ожидание и дисперсию этой случайной величины.
Задача 3. В страховом обществе застраховано 10000 лиц одного возраста одной социальной группы. Вероятность смерти в течение года для каждого лица р=0,006. Каждый застрахованный вносит 1 января 12 рублей страховых, и в случае его смерти родственники получают от общества 1000 руб. Чему равна вероятность того, что:
а) общество потерпит убытки;
б) общество получит прибыль, не меньшую 40000 руб.?
Задача 4. Случайная величина Х задана функцией распределения F (x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.
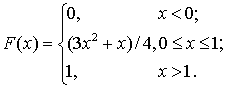
Задача 5. Известны математическое ожидание а и среднее квадратическое отклонение нормально распределенной случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (,); а=6, =3, =2, =11.
Задача 6. На поле 1500 Га для определения средней урожайности с каждого гектара взята проба с 1м2. Оценить вероятность того, что отклонение средней выборочной урожайности отличается от средней урожайности по всему полю не более, чем на 0,1 ц, если по каждому гектару поля дисперсия её не превышает 5.
Задача 7. Дана двумерная дискретная случайная величина (X, Y). Найти ее корреляционную матрицу.
-
X\Y
-2
0
-2
0,25
0,15
-1
0,3
0,1
3
0,15
0,05