8. Варианты контрольной paбoты № 1 по теории вероятностей вариант 1

Задача 1. Три контролера проверяют стандартность однотипных деталей. Один из них успевает проверить вдвое больше, чем остальные (поровну) вместе. Вероятности допустить ошибку у них соответственно равны 0,5; 0,1; 0,2. Пропущенная деталь оказалась с браком. Какова вероятность, что ее пропустил первый контролер?

Задача 2. Производится два независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,7. Случайная величина X – разность между числом попаданий и числом промахов. Составить закон распределения случайной величины X и вычислить числовые характеристики.

Задача 3. Известно, что 3/5 рабочих никелевого завода имеет среднее образование. Для некоторого обследования наудачу выбирается 1500 человек. Найти вероятность того, что 920 человек из них имеют среднее образование.

Задача 4. Случайная величина Х задана функцией распределения F (x). Найти плотность распределения вероятности, математическое ожидание и дисперсию случайной величины.

Задача 5. Известны математическое ожидание а и среднее квадратическое отклонение  нормального распределения случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (,); a= 7, = 2, =3, =10.

Задача 6. Дисперсия каждой из 400 независимых случайных величин не превышает 0,25. Какой величины не должен превышать модуль разности средней арифметической этих случайных величин и средней арифметической их математических ожиданий, чтобы вероятность такого отклонения превышала 0,99.

Задача 7. Дана двумерная дискретная случайная величина (X, Y). Найти ее корреляционную матрицу.

X\Y	-1	1	2
-3	0,1	0,15	0,05
1	0,2	0,25	0,25

Вариант 2

Задача 1. В ящике находятся изделия, которые изготовили на трех станках, причем 20 изготовлены на первом станке, 18 - на втором и 14 - на третьем. Вероятности того, что изделия, изготовленные на первом, втором и третьем станках отличного качества соответственно равны 0,7; 0,85; 0,9. Извлеченное наудачу изделие оказалось отличного качества. Какова вероятность того, что оно изготовлено на втором станке?

Задача 2. Охотник, имеющий 4 патрона, стреляет в цель до первого попадания (или пока не израсходует все патроны). Вероятность попадания при каждом выстреле – 0,3. Случайная величина X - число израсходованных патронов. Составить закон распределения вероятностей случайной величины X, найти числовые характеристики этой случайной величины.

Задача 3. На проверку всхожести зерна берут 500 зерен. Установлено, что количество всхожих семян составляет 3/4 всего количества зерен. Найти вероятность того, что из взятых 500 зерен 400 окажутся всхожими.

Задача 4. Случайная величина X задана функцией распределения F (x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.

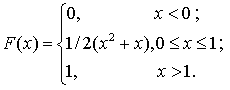
Задача 5. Известны математическое ожидание а и среднее квадратическое отклонение  нормально распределенной случайной величины X. Найти вероятность попадания этой величины в заданный интервал a= 8, = 4, =4, =9.

Задача 6. Имеется 3200 независимых случайных величин, дисперсии которых ограничены. Какой должна быть нижняя граница этих дисперсий, чтобы отклонение средней арифметической данных случайных величин от среднего арифметического их математических ожиданий не превышало по абсолютной величине 0,25 с вероятностью, большей 0,96.

Задача 7. Дана двумерная дискретная случайная величина (Х, Y). Найти ее корреляционную матрицу.

X\Y	1	3
-2	0,1	0,1
1	0,2	0,3
2	0,1	0,2