Вопросы для самопроверки

1. Чем отличается выборочная совокупность от генеральной совокупности распределения?

2. Что называется эмпирической функцией распределения?

3. Что такое гистограмма?

4. Сформулируйте понятие точечной оценки параметра закона распределения случайной величины?

5. Какая оценка называется несмещенной? состоятельной? эффективной?

6. Какая оценка для математического ожидания обладает свойствами несмещенности и состоятельности в случае n независимых равноточных измерений?

7. Какая оценка для дисперсии распределения обладает свойствами несмещенности и состоятельности в случае n независимых равноточных измерений?

8. Что называется доверительным интервалом для точечной оценки параметра распределения?

9. Как находится доверительный интервал для оценки математического ожидания случайной величины, распределенной по нормальному закону с известным ? неизвестным ?

10. В чем состоит идея метода моментов для нахождения оценок параметров распределения?

11. В чем состоит идея метода наибольшего правдоподобия для нахождения оценок параметров распределения?

12. Найти функцию правдоподобия для случайной величины дискретного типа и для случайной величины непрерывного типа.

13. В чем состоит различие задания выборочных данных системы случайных величин в случае несгруппированных и сгруппированных данных?

14. Написать уравнение прямых линий регрессии Y на X и X на Y по выборочным данным.

15. Какой вид имеет оценка для коэффициента корреляции двух случайных величин?

16. Сформулируйте задачу статистической проверки гипотез. Приведите примеры.

17. Что такое критерий и критическая область в методе статистической проверки гипотез?

18. Какими могут быть критические области и как они находятся?

19. В чем сущность, идея метода проверки гипотезы о значимости выборочного коэффициента корреляции? Какой критерий используется?

20. В чем сущность метода проверки гипотезы о распределении генеральной совокупности с помощью критерия согласия К. Пирсона (критерия ²) в случае полностью определенного гипотетического распределения?

21. В чем сущность метода проверки гипотезы о распределении генеральной совокупности с помощью критерия ² в случае, когда гипотетическое распределение содержит некоторое количество неизвестных параметров?

22. Как производится сравнение генеральных средних двух распределенных по нормальному закону случайных величин методом статистических гипотез? Какой критерий при этом используется?

23. Как производится сравнение генеральных средних двух произвольно распределенных случайных величин в случае больших независимых выборок методом статистических гипотез?

24. Как производится сравнение генеральных средних двух нормально распределенных случайных величин в случае малых независимых выборок методом статистических гипотез? Какой критерий при этом используется?

25. Как производится сравнение двух дисперсий нормальных генеральных совокупностей методом статистических гипотез? Какой критерий используется?

26. Как производится сравнение наблюдаемой относительной частоты с гипотетической вероятностью события методом статистических гипотез?

Задачи

1. Найти эмпирическую функцию распределения для выборки, представленной статистическим рядом:

Х	2	5	7	8
	1	3	2	4

Ответ:

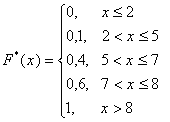
2. Построить гистограмму относительных частот выборки, представленной в виде интервального статистического распределения

I	10-12	12-14	14-16	16-18	18-20	20-22	22-24
ni	2	4	8	12	16	10	3

3. Ниже приведены результаты измерения роста (в см) случайно отобранных 100 школьников в возрасте 14 лет.

Х (рост)	154-158	158-162	162-166	166-170	170-174	174-178	178-182
ni	10	14	26	28	12	8	2

Найти выборочное среднее и несмещенную выборочную дисперсию роста обследованных школьников.

Ответ: .

4. В течение продолжительного срока при анализе данного материала на содержание железа установлено стандартное отклонение 0,12%. Найти с доверительной вероятностью 0,95 доверительный интервал для истинного содержания железа в образце, если по результатам 6 анализов среднее содержание железа составило 32,56 %.

Ответ: I = (32,46; 32,66).

5. Из генеральной совокупности извлечена выборка объема n = 10.

X	-2	1	2	3	4	5
ni	2	1	2	2	2	1

Оценить с доверительной вероятностью 0,95 математическое ожидание нормально распределенного признака генеральной совокупности по выборочному среднему с помощью доверительного интервала

Ответ: = (0,3;3,7).

6. Сырье, поступающее на завод из карьера, содержит два полезных компонента - минералы A и В. Результаты анализов десяти образцов сырья, поступившего в разное время из разных мест карьера, приведены в таблице, где Х и Y - соответственно процентное содержание минералов А и В в образцах.

Номер образца	1	2	3	4	5	6	7	8	9	10
Х	67	54	72	64	39	22	58	43	46	34
Y	24	15	23	19	16	11	20	16	17	13

Найти выборочный коэффициент корреляции и уравнения прямых регрессии Y на Х и Х на Y. Проверить значимость выборочного коэффициента корреляции при .

Ответ:

является значимым.

7. Часы, выставленные в витринах часовых мастерских, показывают случайное время. Некто наблюдал показания 500 часов и получил следующие результаты:

i	0	1	2	3	4	5	6	7	8	9	10	11
	41	34	54	39	49	45	41	33	37	41	47	39

где - номер промежутка от -го часа до -го, , а - число часов, показания которых принадлежали -му промежутку.

Согласуются ли эти данные при уровне значимости  = 0,05 с гипотезой о том, что показания часов равномерно распределены на интервале (0, 12)?

Ответ: согласуются.

8. Распределение числового признака X в выборке определяется следующей таблицей:

I	3,0-3,6	3,6-4,2	4,2-4,8	4,8-5,4	5,4-6,0	6,0-6,6	6,6-7,2
ni	2	8	35	43	22	15	5

При уровне значимости = 0,01 проверить гипотезу о нормальности распределения Х в генеральной совокупности.

9. По двум независимым выборкам, объемы которых соответственно равны m = 60, n = 50, извлеченных из нормальных генеральных совокупностей X и Y, найдены выборочные средние . Генеральные дисперсии известны . При уровне значимости  = 0,01 проверить нулевую гипотезу при конкурирующей гипотезе .

Ответ: нулевая гипотеза отвергается. Z_наб = -12,5; Z_кр = 2,58.

10. По двум независимым выборкам, объемы которых соответственно равны m =5, n=6, извлеченных из нормальных совокупностей Х и Y, найдены выборочные средние и «исправленные» выборочные дисперсии . При уровне значимости  = 0,05 проверить нулевую гипотезу при конкурирующей гипотезе .

Ответ: нет оснований отвергнуть нулевую гипотезу. T_наб = 0,88; t_кр = 2,26.

11. По двум независимым выборкам, объемы которых соответственно равны m = 10, n = 18, извлеченных из нормальных генеральных совокупностей X и Y, найдены «исправленные» выборочные дисперсии и . При уровне значимости  = 0,01 проверить нулевую гипотезу при конкурирующей гипотезе .

Ответ: _наб = 3, _кр = 2,5. Нулевая гипотеза отвергается.

12. По 100 независимым испытаниям найдена относительная частота . По уровню значимости  = 0,05 проверить нулевую гипотезу при конкурирующей гипотезе .

Ответ: наб. = -1,23, кр. = 1,96. Нет оснований отвергнуть нулевую гипотезу.

13. По 20-ти равноточным измерениям физической величины, имеющей нормальный закон распределения, найдено «исправленное» среднее квадратическое отклонение =1,42. Найти точность измерений с надежностью 0,95.

Ответ: .