7.12. Сравнение наблюдаемой относительной частоты с гипотетической вероятностью наступления события

Пусть произведено достаточно большое число испытаний n, в каждом из которых некоторое событие наступает с вероятностью р, которое неизвестно. Требуется по относительной частоте проверить нулевую гипотезу, состоящую в том, что неизвестная вероятность р равна гипотетической вероятности , т.е. . Так как вероятность оценивается по относительной частоте, то требуется установить значимо или незначимо отличается относительная частота от гипотетической вероятности. В качестве критерия возьмем следующую случайную величину:

. (7.12.1)

Известно, что при случайная величина сходится по вероятности к . Нетрудно показать, что при больших n случайную величину К можно считать приближенно распределенной по нормальному закону . Критическая область строится в зависимости от вида конкурирующей гипотезы.

Двусторонняя критическая область

Пусть при конкурирующей гипотезе . Задаем уровень значимости ; двусторонняя критическая область определяется из условия, чтобы вероятность попадания критерия в эту область (в предположении справедливости нулевой гипотезы, была равна ). Левую и правую критические точки выбираем из условий

P (K<k_лев.кр)=/2, P (K>k_пр.кр)=/2.

В силу симметрии закона распределения К критические точки k_лев.кр и k_пр.кр симметричны относительно точки z=0 и обозначаются соответственно -k_кр и k_кр (рис. 7.12.1); поэтому задача сводится к нахождению k_кр.

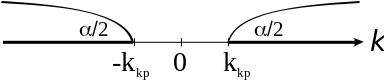
Рис. 7.12.1

Так как P (0<K<k_кр)=Ф (k_кр) и P (0<K<k_кр)+P (K>k_кр)=1/2,

P (0<K<k_кр)=Ф (k_кр), P (K> k_кр)=/2, то

Ф (k_кр)=(1-)/2. (7.12.2)

Из равенства (7.12.2) по табл. 4 приложения определяется k_кр. Таким образом, критическая область определяется неравенствами: К<- k_кр, K> k_кр.

По формуле (7.12.1) и данным задачи определяем K_наб. Если |K_наб | < k_кр, нулевая гипотиза принимается; если же | K_наб | > k_кр, – принимается Н_0.

Правосторонняя критическая область

Пусть Н₀: р=р₀ при конкурирующей гипотезе Н₁: р > р₀. В этом случае критическая область определяется из условия: P (K> k_кр)=.

Так как P (0<K<k_кр) + P (K>k_кр) = 1/2, то

Ф (k_кр)=1/2-. (7.12.3)

находим из формулы (7.12.3) по табл. 4 приложения. Таким образом, правосторонняя критическая область определяется неравенством (рис. 7.12.2).

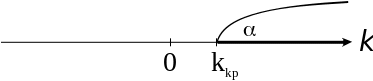
Рис. 7.12.2

Если K_наб > k_кр – нулевая гипотеза отвергается.

Если K_наб < k_кр – нулевая гипотеза принимается.

Левосторонняя критическая область

Пусть при нулевой гипотезе конкурирующая имеет вид . В этом случае речь идет о левосторонней критической области, определяемой равенством P (K< k_кр) = . (рис. 7.12.3)

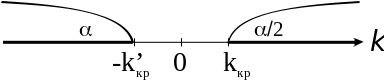
Рис. 7.12.3

В силу симметричности распределения K относительно , заключаем, что k’_кр симметрична такой k_кр>0, что P (K > k_кр) = ., т.е. . Следовательно, находим сначала вспомогательную точку по равенству , а затем полагаем k’_кр = –k_кр.

Если – нулевая гипотеза отвергается.

Если – нулевая гипотеза принимается.

Задача 7.12.1. По 100 независимым испытаниям найдена относительная частота . При уровне значимости =0,05 проверить нулевую гипотезу при конкурирующей гипотезе .

Решение. Находим сначала по табл. 4 приложения критическую точку для двусторонней критической области из равенства (6.4.2).

.

Находим по формуле (7.12.1) наблюдаемые значения критерия :

.

Очевидно, . Нет оснований отвергнуть нулевую гипотезу.