1.4. Аксиоматическое введение вероятности

Пусть Ω – пространство элементарных событий, F – алгебра событий. Тогда следующие 5 условий образуют систему аксиом вероятности.

1. F является σ-алгеброй случайных событий.

F будем называть σ-алгеброй событий, если для любой счетной последовательности случайных событий {A_i}, i = 1,2,…, A_iF, их объединение 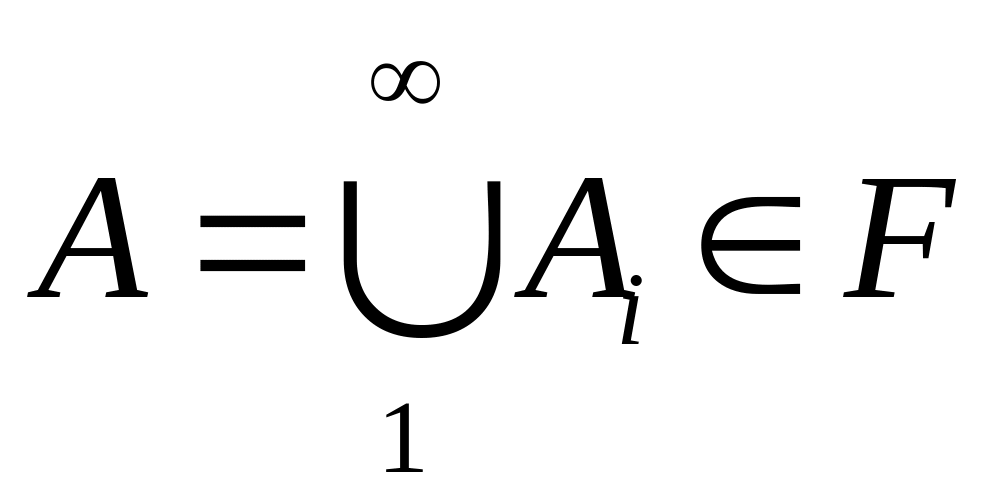, т.е. является случайным событием. Из принципа двойственности следует, что и .

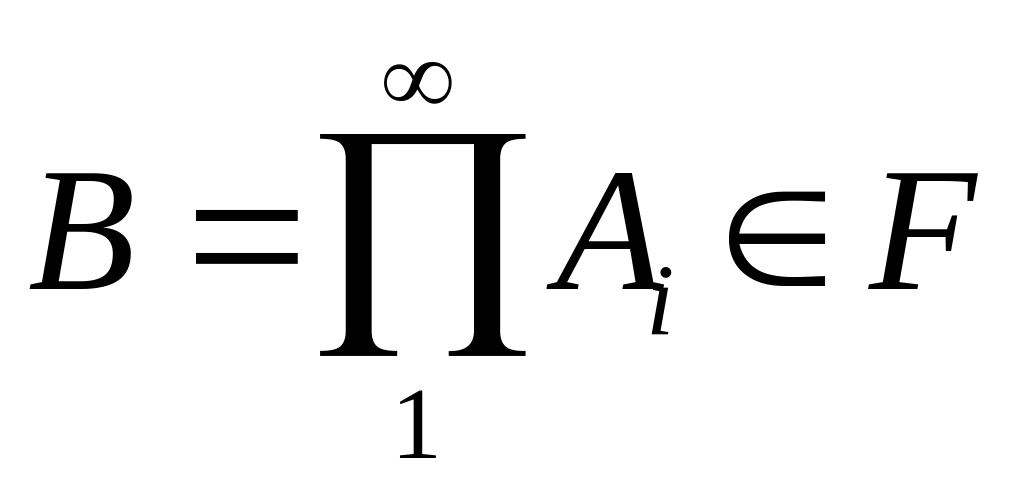2. На σ-алгебре F определена функция Р(·), принимающая для любых 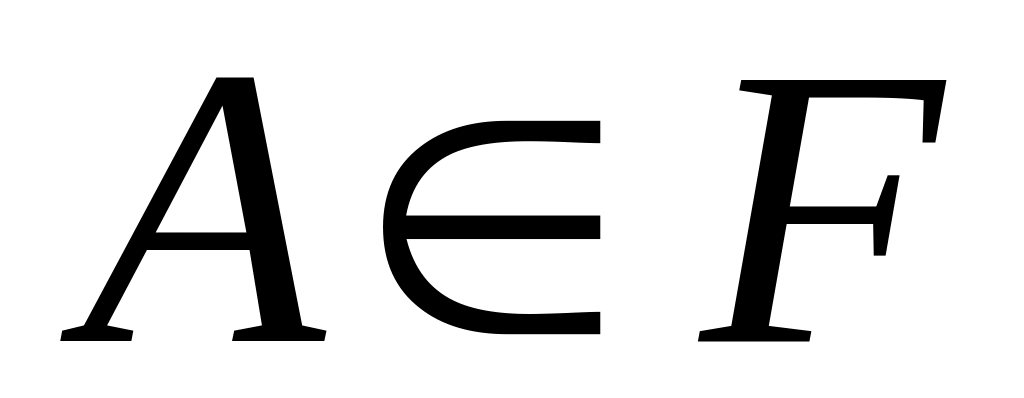неотрицательные значения, т.е. Р(А) 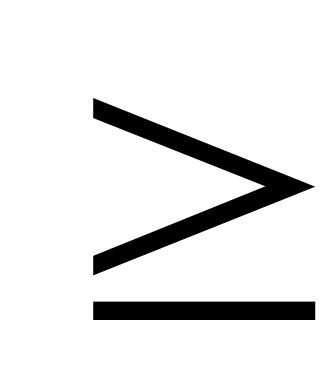0.

3. Для любых двух несовместных событий А,ВF имеет место равенство

Р(А+В)=Р(А)+Р(В), (1.4.1)

называемое аксиомой сложения вероятностей.

4. Для произвольной счетной последовательности {A_i} несовместных событий имеет место равенство

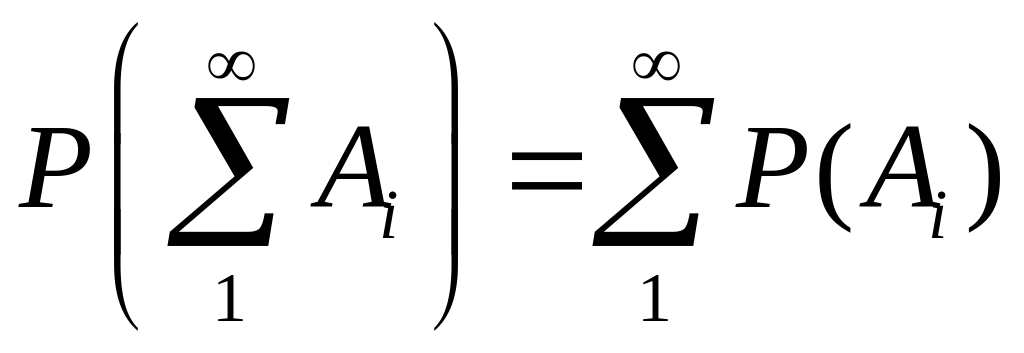. (1.4.2)

Эта теорема определяет счетную аддитивность вероятности, иначе называемую аксиомой непрерывности вероятности.

5. Р(Ω)=1.

Пространство элементарных событий Ω, σ-алгебра событий F и вероятность Р(·) на F, удовлетворяющие 5-ти аксиомам вероятности определяют вероятностное пространство, обозначаемое (Ω, F, P).

1.5. Теоремы о вероятностях случайных событий

Из аксиом вероятности, сформулированных в предыдущем параграфе, вытекает ряд следующих теорем.

Теорема 1. Для любого события имеет место следующее равенство:

. (1.5.1)

Доказательство. Действительно, так как , равенство (1.5.1) следует из аксиом 3 и 5 вероятности.

Теорема 2. Если , то Р(А\В)=Р(А)–Р(В).

Доказательство. Имеем очевидное равенство А=В+(А\В), где В и А\В являются несовместными событиями. Используя аксиому 3 вероятности, имеем Р(А\В)=Р(А)–Р(В); отсюда вытекает, что .

Теорема 3. Для любых двух случайных событий А и В F имеет место равенство

. (1.5.2)

Доказательство. Если А и В – произвольные случайные события, то ; здесь событие представляется в виде суммы двух несовместимых событий. Используя аксиому 3 вероятности, имеем:

.

Задача 1.5.1. Два стрелка, независимо друг от друга стреляют по одной мишени, произведя залп. Вероятности попадания в мишень для первого стрелка 0,9; для второго – 0,8. Найти вероятность поражения мишени.

Решение. Пусть А – попадание в мишень первого стрелка; В – попадание в мишень второго стрелка. Тогда – поражение мишени (хотя бы одним стрелком). Имеем . Имеем .

Теорема 4. Для произвольных случайных событий А₁, А₂, …, А_n F имеет место равенство

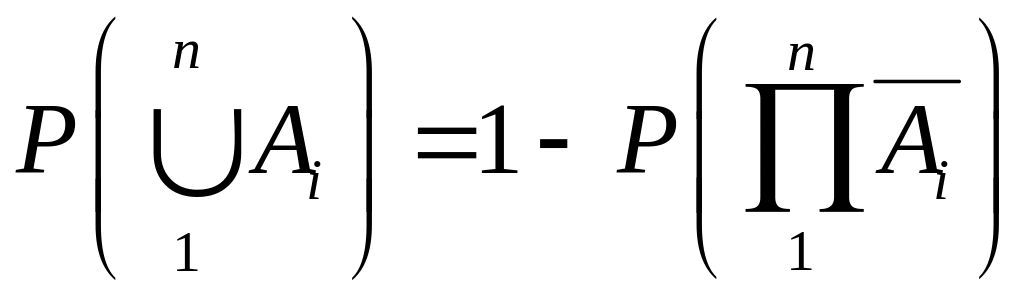. (1.5.3)

Доказательство. Учитывая, что события и являются взаимно противоположными, из теоремы 1 имеем равенство (1.5.3).

Теорема 5. Вероятность невозможного события  равна нулю.

Доказательство. Имеем очевидное равенство  +  = . Отсюда из аксиом 1 и 5 имеем Р()+Р()= Р() или Р()=0.

Теорема 6. Для любого случайного события АF имеем

. (1.5.4)

Доказательство следует сразу же из теоремы 2, если учесть, что А и , отсюда следует (1.5.4).

Пусть имеем вероятностное пространство (, F, Р). Введем условную вероятность события А при условии, что произошло событие В, с помощью следующего равенства:

P(A/B)=P(AB)/P(B), Р(В)>0. (1.5.5)

Аналогично определяется условная вероятность события В при условии, что А произошло:

P(B/A)=P(AB)/P(A), Р(А)>0. (1.5.6)

Из определений (1.5.5) и (1.5.6) следует следующая теорема.

Теорема 7. Для любых случайных событий А,ВF имеет место следующее равенство:

Р(АВ)=Р(B)Р(А/В) или Р(АВ)=Р(А)Р(В/А). (1.5.7)

Эта теорема называется теоремой умножения вероятностей.

Определение 1.5.1. Два случайных события А и В называются независимыми, если вероятность любого из них не изменяется в зависимости от того, произошло другое событие или не произошло.

В случае независимых случайных событий Р(А/В)=Р(А) и Р(В/А)=Р(В); поэтому теорему умножения для независимых случайных событий можно переписать в виде

Р(АВ)=Р(А)Р(В). (1.5.8)

Во многих случаях равенство (1.5.8) используют в качестве определения независимых случайных событий.

Теорема умножения вероятностей может быть обобщена на случай любого конечного числа случайных событий.

Теорема 8. Для любого конечного числа случайных событий А₁, А₂, …, А_nF имеем

Р(А₁А₂…А_n)=Р(А₁)Р(А₂/А₁)Р(А₃/А₁А₂)… Р(А_n/А₁А₂…А_n-1). (1.5.9)

В случае n случайных событий (n>2) следует различать попарную независимость случайных событий, если любые 2 являются независимыми, и независимость в совокупности, если каждое из них и любая комбинация остальных событий есть события независимые. В этом последнем случае теорема умножения (1.5.9) может быть записана так:

Р(А₁А₂…А_n)=Р(А₁)Р(А₂)…Р(А_n). (1.5.10)

Очевидно, что из независимости в совокупности следует попарная независимость случайных событий; однако из попарной независимости случайных событий не следует независимость в совокупности, что подтверждается следующей классической задачей.

Задача Бернштейна. Опыт заключается в бросании правильного тетраэдра, 3 грани которого окрашены соответственно в синий, красный, зеленый цвета, четвертая же грань окрашена всеми этими цветами одновременно. Если С, К, З – случайные события, заключающиеся в том, что тетраэдр падает на грани, окрашенные соответственно в синий, красный и зеленый цвета, то можно показать, что эти события попарно независимы, но не являются независимыми в совокупности.

Действительно, Р(СК)=1/4=0,5∙0,5=Р(С)Р(К); следовательно, события С и К независимы. Аналогично Р(СЗ)=Р(С)Р(З) и Р(КЗ)=Р(К)Р(З). Таким образом, случайные события С,К,З – попарно независимы. Но Р(СКЗ)=1/4≠1/8=P(С)P(К)P(З); следовательно, они не являются независимыми в совокупности.

Задача 1.5.2. Студент пришел на экзамен, зная лишь 25 из 30 вопросов. В билете 3 вопроса. Найти вероятность того, что студент ответит на все три вопроса билета.

Решение. Пусть А – случайное событие, заключающееся в том, что студент ответит на 1-й вопрос; В – студент ответит на 2-й вопрос; С – студент ответит на 3-й вопрос. По теореме умножения вероятностей для трех событий имеем Р(АВС)=Р(А)Р(В/А)Р(С/АВ). Поэтому

P(ABC)=(25/30)(24/29)(23/28)=115/203.