7.5. Нахождение оценки для коэффициента корреляции двух случайных величин

Пусть над системой случайных величин (X, Y) произведено в одинаковых условиях n независимых опытов. Результаты опытов:

(7.5.1)

являются независимыми системами случайных величин, математические ожидания, дисперсии и корреляционные моменты которых одинаковы, т.е.

.

Требуется на основании статистических данных (7.5.1) найти оценки этих числовых характеристик системы.

Для математических ожиданий и дисперсий компонент системы имеем известные формулы для их оценок:

. (7.5.2)

Так как корреляционный момент равен , будем искать оценку для него в виде

(7.5.3)

причем в силу равноточности измерений . Неизвестный коэффициент определяется из условия несмещенности оценки (7.5.3):

.

После преобразования выражений, стоящих под знаком суммы, получим несмещенную, состоятельную оценку для корреляционного момента

(7.5.4)

Выборочный коэффициент корреляции определяется по формуле

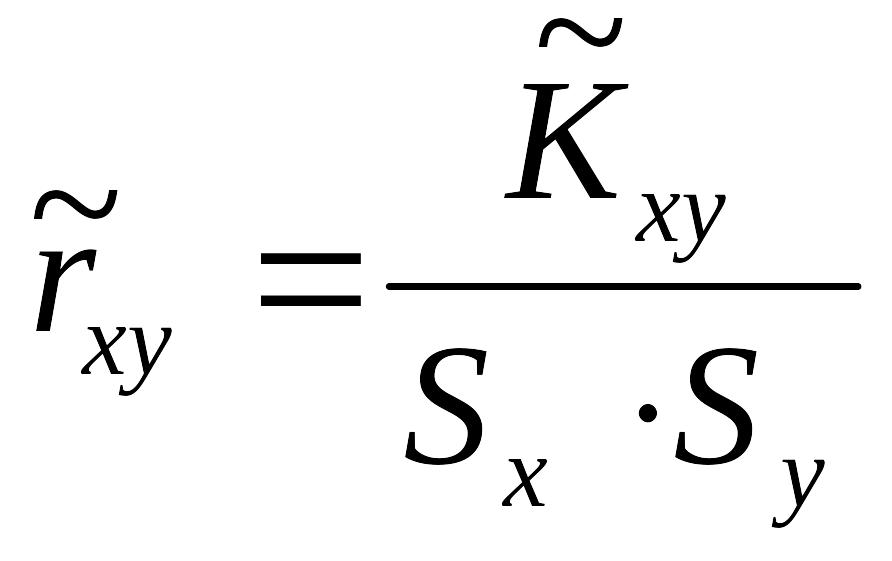. (7.5.5)

Вместо формул (7.5.4) и (7.5.5) для выборочного коэффициента корреляции полезно иметь расчетные формулы, использующие статистические данные (7.5.1).

Имеем

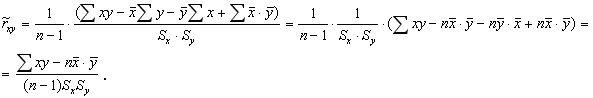
Таким образом, для выборочного коэффициента корреляции имеем следующую формулу:

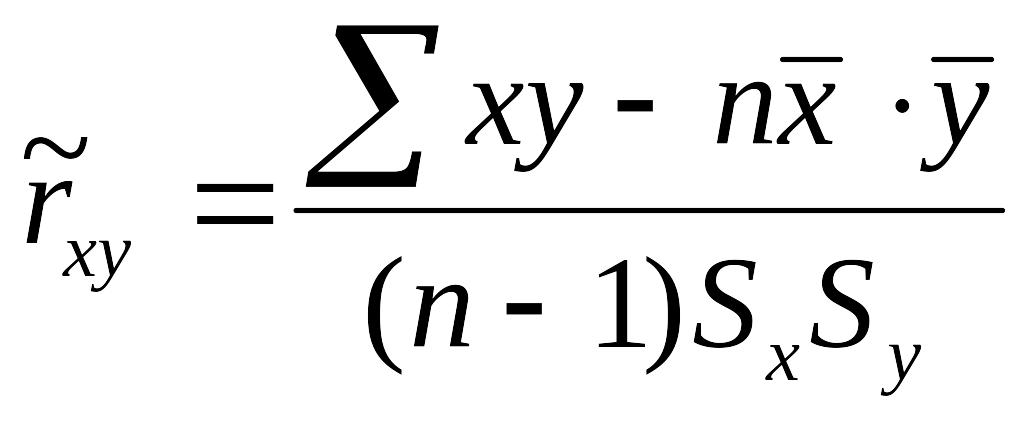. (7.5.6)

Если использовать вместо “исправленных” выборочных дисперсий и выборочные дисперсии и , то с использованием формулы их связи вместо формулы (7.5.6) получим:

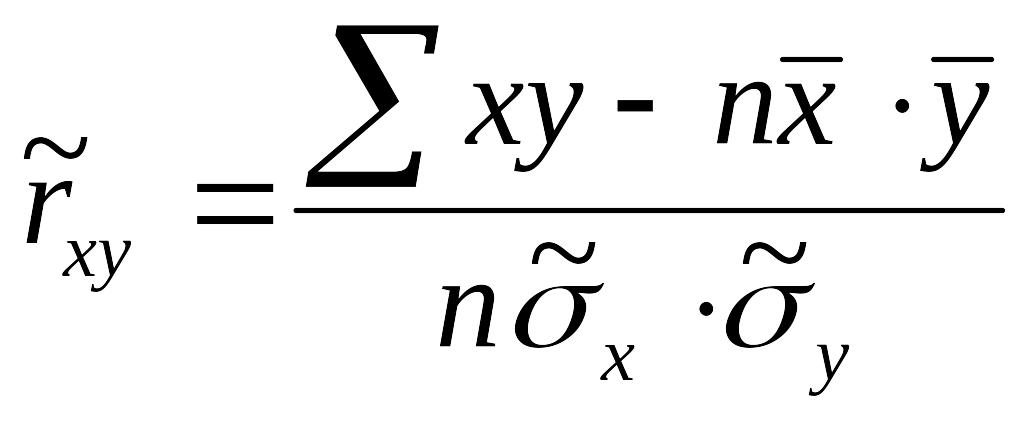. (7.5.7)

Если использовать сгруппированные статистические данные, несложно получить вместо (7.5.7) для выборочного коэффициента корреляции следующую расчетную формулу:

. (7.5.8)

Выборочный коэффициент корреляции является оценкой коэффициента корреляции .

Задача 7.5.1. Используя данные задачи 7.4.1, найти выборочный коэффициент корреляции.

Решение. По полученным данным вспомогательной таблицы решения задачи 7.4.1, найдем сначала выборочные средние , а также выборочные дисперсии :

_.

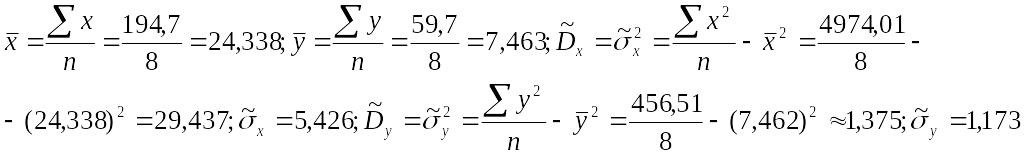Используя формулу (7.5.7), имеем .

7.6. Статистическая проверка гипотез. Статистическая гипотеза. Нулевая и конкурирующая гипотеза. Статистический критерий. Критическая область

При исследовании случайной величины X на основании статистических данных довольно часто необходимо знать закон распределения генеральной совокупности или, если закон распределения известен, его параметры. В этих случаях выдвигают гипотезы о виде предполагаемого распределения или о предполагаемой величине параметра известного распределения.

Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Нулевой (основной) называют выдвинутую гипотезу . Конкурирующей (альтернативной) называют гипотезу , которая противоречит основной.

Например, если нулевая гипотеза состоит в предположении, что математическое ожидание нормального распределения равна 5, то конкурирующая гипотеза состоит в предположении, что . Кратко это записывают так: ; .

Проверку выдвинутой гипотезы осуществляют статистическими методами, поэтому ее называют статистической проверкой гипотез. В итоге статистической проверки гипотезы может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов:

1) ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза;

2) ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Правильное решение может быть принято также в двух случаях:

1) гипотеза принимается, причем она и в действительности правильная;

2) гипотеза отвергается, причем она и в действительности неверна.

Вероятность совершить ошибку первого рода (отвергнуть правильную гипотезу) принято обозначать через ; ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если, например, принят уровень значимости 0,01, то это значит, что имеется риск отвергнуть правильную гипотезу в одном случае из ста.

Статистическим критерием (или просто критерием) называют случайную величину , которая служит для проверки нулевой гипотезы. Часто критерием служит случайная величина, распределенная по закону ² или закону Стьюдента.

Наблюдаемым значением _наб называют значение критерия, вычисленное по выборке, т.е. получают частное (наблюдаемое) значение критерия, вычисленное с помощью частных значений, входящих в критерий величин. После установления множество его значений разбивается на два пересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, другое – при которых она принимается.

Критической областью называют множество значений критерия, при которых нулевую гипотезу отвергают.

Областью допустимых значений (область принятия гипотезы) называют множество значений критерия, при которых нулевую гипотезу принимают.

Идея метода статистических гипотез состоит в следующем: если наблюдаемое значение критерия принадлежит критической области – нулевую гипотезу отвергают; если наблюдаемое значение принадлежит области допустимых значений – нулевую гипотезу принимают.

Критическая область и область принятия гипотезы представляют собой интервалы, поэтому существуют точки, которые их разделяют.

Критическими точками _кр называют точки, разделяющие критическую область и область принятия гипотезы.

Различают односторонние критические области (правосторонние и левосторонние) и двусторонние.

Правосторонней называют критическую область, определяемую неравенством _кр, где _кр > 0 (рис. 7.6.1, а).

Л

Рис. 7.6.1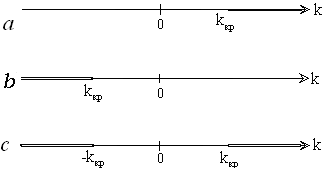

евосторонней называют критическую область, определяемую неравенством _кр, где _кр < 0 (рис. 7.6.1,b).

Двусторонней называют критическую область, определяемую неравенствами , где . В частности, если критические точки симметричны, двусторонняя критическая область определяется неравенствами _кр, _кр или _кр (рис. 7.6.1, c).

Нахождение правосторонней критической области

Как известно, правосторонняя критическая область определяется неравенством _кр. Для нахождения критической точки _кр задаем достаточно малую вероятность – уровень значимости . Затем находим критическую точку исходя из требования, чтобы при условии справедливости нулевой гипотезы вероятность того, что _кр., была равна

_{кр = .} (7.6.1)

Обоснование равенства (7.6.1) заключается в следующем: так как вероятность события _кр мала ( – малая вероятность), то при справедливости нулевой гипотезы это событие не должно наступить в единичном испытании; если же оно произошло, т.е. наблюдаемое значение критерия оказалось больше _кр, то это можно объяснить тем, что нулевая гипотеза ложна и должна быть отвергнута. С другой стороны, наблюдаемое значение может оказаться большим _кр не потому, что нулевая гипотеза ложна, а по другим причинам (малый объем выборки, недостатки методики эксперимента и др.). В этом случае, отвергнув нулевую гипотезу совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости .

Критическая точка _кр находится по таблицам критических точек распределения критерия и заданному уровню значимости .

Если критическая точка _кр уже найдена, по данным выборки вычисляют наблюдаемое значение критерия _наб и, если окажется, что _наб > _кр - нулевую гипотезу отвергают; если же _наб < _кр – нет оснований отвергать нулевую гипотезу.

Нахождение левосторонней критической области

Левосторонняя критическая область определяется неравенством < _кр( _кр<0). Критическую точку _кр находят исходя из требования, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий примет значение, меньшее _кр, была равна принятому уровню значимости :

_кр . (7.6.2)

Если _{наб кр} – нулевая гипотеза отвергается, если _{наб >} k_кр – нет оснований отвергать нулевую гипотезу.

Нахождение двусторонней критической области

Двусторонняя критическая область определяется неравенствами ( ). Задаем уровень значимости . Критические точки и находят исходя из требования, чтобы при справедливости нулевой гипотезы выполнялось равенство

. (7.6.3)

Ясно, что критические точки и могут быть выбраны бесконечным числом способов. Если распределение является симметричным относительно , выбирают симметричные критические точки: _кр, _кр, ( _кр > 0). В этом случае _кр) _кр), и поэтому

_кр) . (7.6.4)

Из соотношения (7.6.4) определяют _кр. После ее нахождения находят _наб и, если _{наб кр} – нулевую гипотезу отвергают; если _{наб кр} – нет оснований отвергать нулевую гипотезу.