1. Нахождение параметров выборочных уравнений прямой линии регрессии по несгруппированным данным

Пусть в результате n независимых опытов получены n пар значений системы ( ): , которые могут быть заданы табл. 7.5.1. По этим статистическим данным найдем сначала параметры (коэффициенты) уравнения (7.4.3) регрессии Y на X: .

Так как различные значения X и соответствующие им значения наблюдались по одному разу, то группировать данные нет необходимости; также нет надобности использовать понятие условной средней, поэтому уравнение (7.4.3) можно записать

. (7.4.5)

Подберем параметры и так, чтобы точки , построенные по данным наблюдениям на плоскости , лежали как можно ближе к прямой (7.4.5). Разность является отклонением ординаты , вычисленной с помощью уравнения (7.4.5) при от наблюдаемой ординаты, соответствующей значению . Используем в дальнейшем метод наименьших квадратов, а именно подберем параметры и так, чтобы сумма квадратов отклонений была минимальной, т.е. составим функцию (вместо будем писать ): .

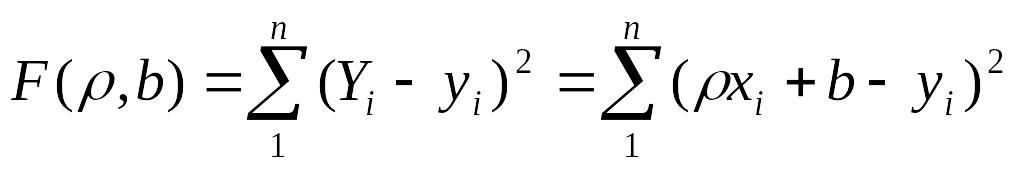Исследуя функцию на минимум, приравняем нулю ее частные производные первого порядка:

, .

Выполняя в последних уравнениях элементарные преобразования и применяя безындексную форму (вместо пишем ), получим систему двух линейных уравнений относительно и :

. (7.4.6)

Решив эту систему, получим:

, . (7.4.7).

Аналогично можно найти выборочные уравнения прямой линии регрессии X на Y:

. (7.4.8)

Формулы для параметров и имеют вид

, (7.4.9)

2. Нахождение параметров выборочных уравнений прямой линии регрессии по сгруппированным данным

Пусть теперь статистические данные сгруппированы и заданы в виде корреляционной табл. 7.5.2. Перепишем систему уравнений (7.4.6) так, чтобы она отражала данные корреляционной таблицы. Для этого учтем следующие тождества:

.

В результате вместо системы (7.4.6) получим систему уравнений:

^(7.4.10)

Решив эту систему, найдем параметры и уравнения прямой линии регрессии:

, (7.4.11)

, . (7.4.12)

Однако иногда уравнение регрессии (7.4.11) удобно записать в другой форме, вводя выборочный коэффициент корреляции. Найдя из второго уравнения (7.4.10) и подставив его в уравнение (7.4.11), получим:

. (7.4.13)

Если ввести соотношение , где

, (7.4.14)

является выборочным коэффициентом корреляции, уравнение (7.4.13) может быть представлено в следующем виде:

. (7.4.15)

Оно называется выборочным уравнением регрессии Y на X.

Аналогично находится выборочное уравнение линейной регрессии X на Y:

. (7.4.16)

Задача 7.5.1. Методами корреляционного анализа исследовать зависимость между урожайностью пшеницы и картофеля на соседних участках на основании статистических данных (США). Построить выборочное уравнение линейной регрессии.

Годы	1926	1927	1928	1929	1930	1931	1932	1933
Урожайность пшеницы (ц)	20,1	23,6	26,3	19,9	16,7	23,2	31,4	33,5
Урожайность картофеля (т)	7,2	7,1	7,4	6,1	6,0	7,3	9,4	9,2

Решение: Составим вспомогательную таблицу

i
1	20,1	7,2	404,01	51,84	144,72
2	23,6	7,1	556,96	50,41	167,56
3	26,3	7,4	691,69	54,76	194,62
4	19,9	6,1	396,01	37,21	121,39
5	16,7	6,0	278,89	36,0	100,2
6	23,2	7,3	538,24	53,29	169,36
7	31,4	9,4	985,96	88,36	295,16
8	33,5	9,2	1122,25	84,64	308,2
	= 194,7	= 59,7	= 4974,01	= 456,51	= 1501,21

Выборочное уравнение линейной регрессии Y на X имеет вид

,

коэффициенты которого и вычисляются по формулам (7.4.7).

Используя вспомогательную таблицу, получим

, .

Таким образом, уравнение линейной регрессии Y на X имеет вид

.

Аналогично уравнение линейной регрессии X на Y имеет вид

,

где коэффициенты и вычисляются по формуле (7.4.9), имеем

, .

Таким образом, уравнение линейной регрессии X на Y имеет вид

.