3. Доверительные интервалы для оценки среднего квадратического отклонения  нормального распределения

Пусть исследуемая случайная величина X генеральной совокупности распределена по закону N (a,). По статистическим данным найдено “исправленное” среднее квадратическое отклонение S. Требуется найти для него доверительный интервал с надежностью .

Требуется найти такое  > 0, чтобы выполнялось равенство

. (7.3.12)

Неравенство |-S|< с помощью ряда равносильных преобразований можно переписать в виде

.

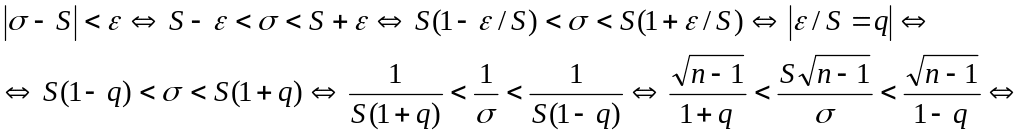
Поэтому равенство (7.3.14) можно переписать в виде

P (|-S|<)=P ( << ) = , (7.3.13)

где

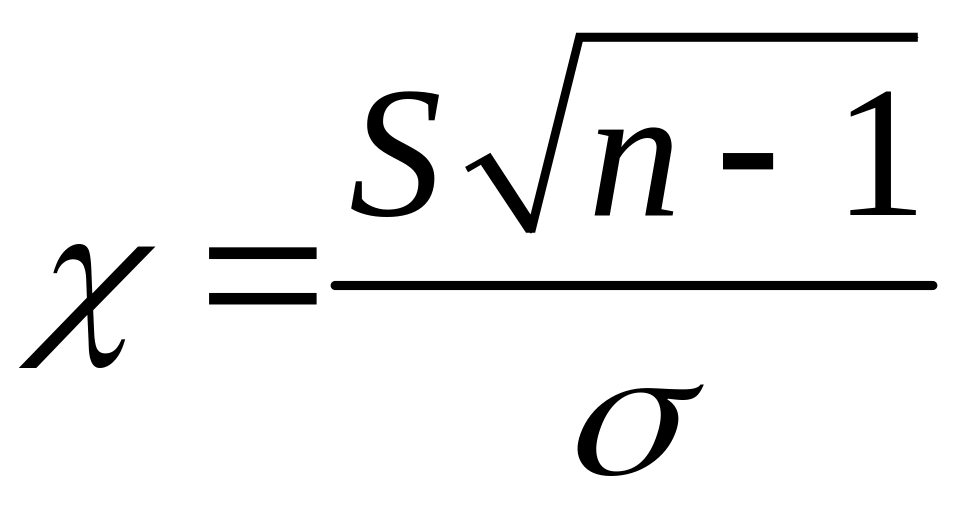. (7.3.14)

Случайная величина (7.3.14) распределена по закону (имеет - распределение) с степенями свободы. Плотность вероятности -распределения с (n-1) степенями свободы имеет вид

Тогда равенство (7.3.13) можно переписать в виде . Из этого уравнения по заданным и можно найти ; для этого используется табл. 6 вероятности попадания случайной величины с - распределением в заданный интервал, зависящий от . После нахождения доверительный интервал определяется равенством

. (7.3.15)

Задача 7.3.4. Количественный признак генеральной совокупности распределен по нормальному закону N (a,). По выборке объема найдено “исправленное” среднее квадратическое отклонение . Найти доверительный интервал для этой оценки с надежностью .

Решение. По табл. 6 приложения по и найдем . Доверительный интервал имеет вид I_ = (1,24(1–0,44); 1,24(1+0,44)) = (0,69;1,79).

Замечание. В теории измерений принято точность измерений (точность измерительной системы) характеризовать с помощью . Для оценки  используют “исправленное” среднее квадратическое отклонение . Поэтому для оценки точности измерений применяется доверительный интервал для , теория построения которого изложена выше.

7.4. Построение прямых линий регрессии по выборочным данным

Две случайные величины могут быть связаны либо функциональной зависимостью, либо быть независимыми, либо связаны зависимостью другого рода, называемой статистической (иначе стохастической). Как правило, функциональная зависимость реализуется редко, так как одна или две случайные величины подвержены действию многих случайных факторов. Случайные величины независимы, если закон распределения одной из них не зависит от того, какие значения принимает другая случайная величина.

Статистической называется такая зависимость, при которой изменение одной из них влечет за собой изменение распределения другой. В частности, если при изменении одной из величин изменяется среднее значение другой, статистическую зависимость называют корреляционной.

Приведем примеры статистической зависимости.

Примеры. Рост X школьников и их возраст Y; месячная зарплата рабочих предприятия X и их месячный расход на бензин Y; тоннаж X, перевезенный за определенный период времени товарными поездами по железной дороге и Y – автотранспортом; количество удобрений X, внесенных на 1 га и урожай Y с этого участка.

О влиянии курения на рак легких. Статистические данные указывают, что процент заболевания раком легких среди тех, кто выкуривает много сигарет в день, гораздо выше, чем среди тех, кто курит мало или не курит вообще. Это указывает на связь, но не на причину заболевания. Не может ли совершенно другая причина вызывать как интенсивное курение, так и рак легких без какой-либо причинно-следственной связи между ними? Могут существовать, например, генетические особенности, которые делают человека более восприимчивым к раку легких и в то же время служат причиной вспыльчивого характера, а поэтому склонности к курению для успокоения нервов? Р. Фишер, известный как генетик не меньше, чем как статистик, рассуждал практически также.

Роль табака как фактора, вызывающего рак легких, была установлена точно лишь тогда, когда из него выделили канцерогены-вещества, тесно связанные со смолой, содержащейся в табаке; было также доказано, что они легче поглощаются организмом из сигарет, чем из сигар или трубочного табака. Таким образом, биохимические исследования подтверждают предполагаемую статистическую связь между курением и раком легких.

Пусть изучается система количественных признаков . В результате опытов выборочные данные могут быть несгруппированными и сгруппированными.

В первом случае (несгруппированных данных) в результате n независимых опытов получены n пар чисел: , которые могут быть представлены в виде таблицы:

Таблица 7.4.1

X			...
Y			...

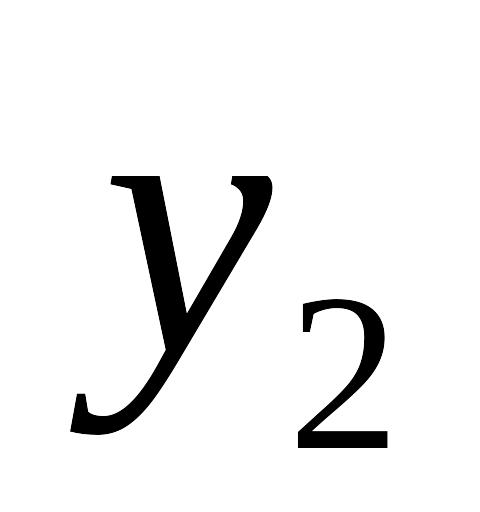
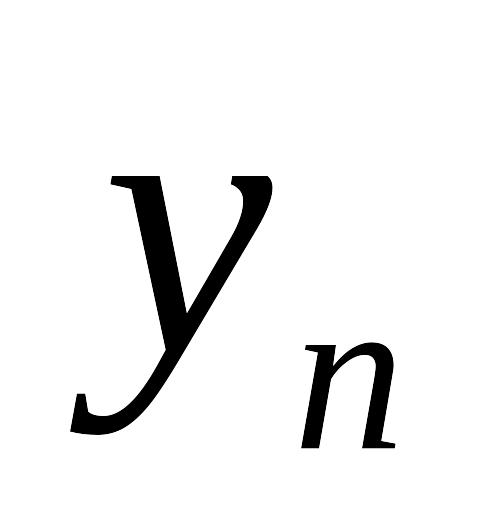
Во втором случае (случай сгруппированных данных) мы имеем дело с корреляционной таблицей. В ней перечислены значения случайных величин Х и У, а также их частоты , равные числу появлений в выборке пары ( )(табл. 7.4.2).

Если количество значений X и Y велико или эти величины распределены непрерывно, то производится группировка их значений по интервалам. В этом случае и представляют собой середины соответствующих интервалов:

Таблица 7.4.2

X/Y	y1	y2	...	yj	...	yl	nx
x1	n11	n12	...	n1j	...	n1l
x2	n21	n22	...	n2j	...	n2l
...	...	...	...	....	...	...	...
xi	ni1	ni2	...	nij	...	nil
...	...	...	...	...	...	...	...
xk	nk1	nk2	...	nkj	...	nkl
ny			...		...		n

Корреляционная таблица содержит всю информацию, полученную в результате выборки наблюдаемых величин X и Y объемом n.

Условным средним называют среднее арифметическое наблюдавшихся значений Y, соответствующих X = x.

Условным средним называют среднее арифметическое наблюдавшихся значений X, соответствующих Y= y.

С помощью корреляционной табл. 7.4.2 для каждого значения можно построить условное эмпирическое распределение случайной величины Y. В табл. 7.4.3 перечислены все значения случайной величины Y, а также соответствующие частоты:

Таблица 7.4.3

Y			.....		.....
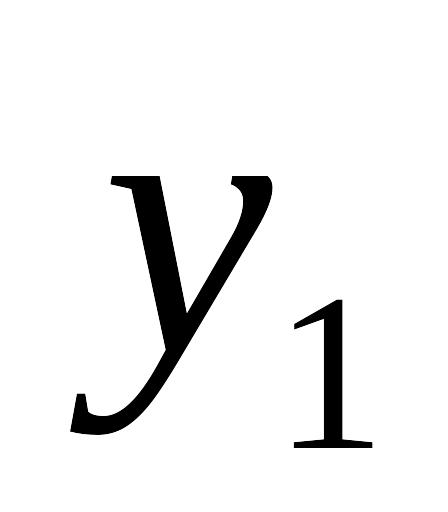
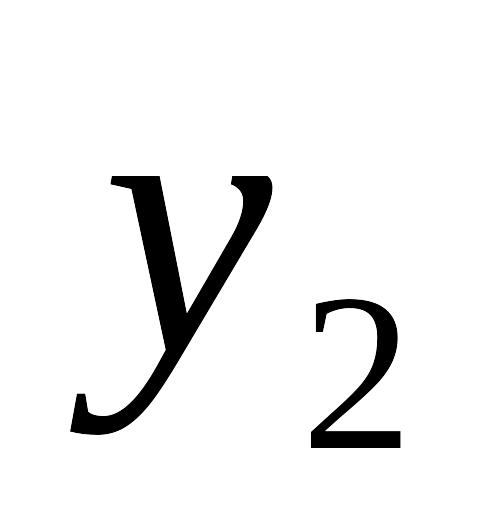
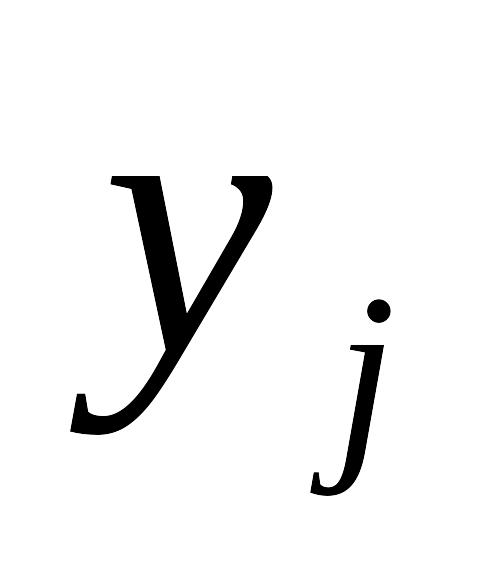
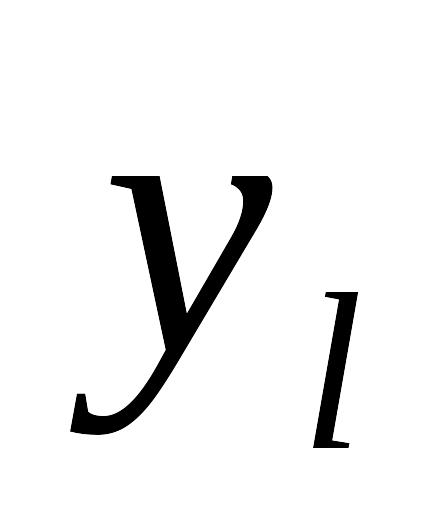
nx			.....		.....

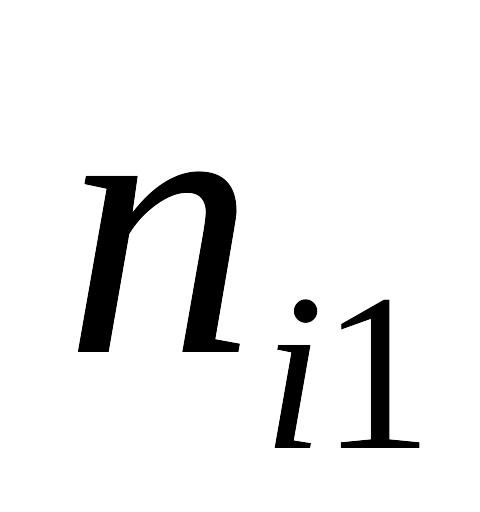
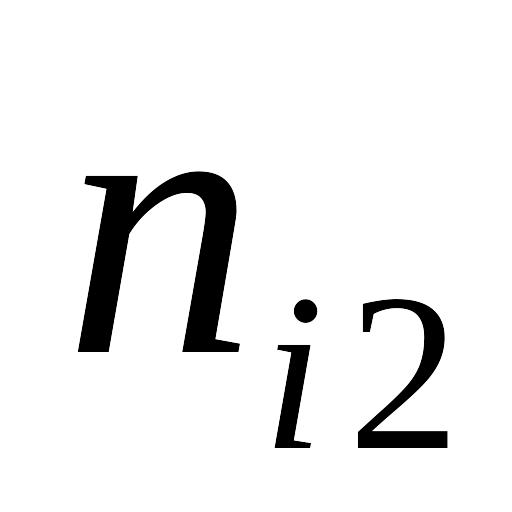
На основании табл. 7.4.3 можно определить условное среднее :

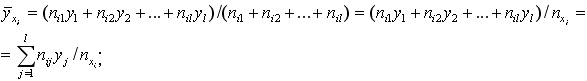
Если подобным образом определить условные средние значения Y , то можно составить таблицу, в первой строке которой перечислены все встречающиеся в выборке значения величины X, а во второй - соответствующие условные средние значения величины Y (Табл. 7.4.4).

Таблица 7.4.4

X			.....		.....
			.....		.....

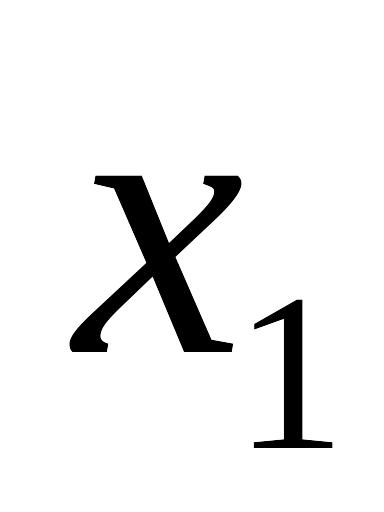
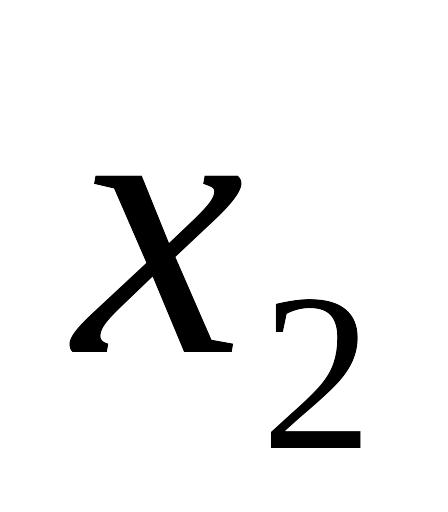
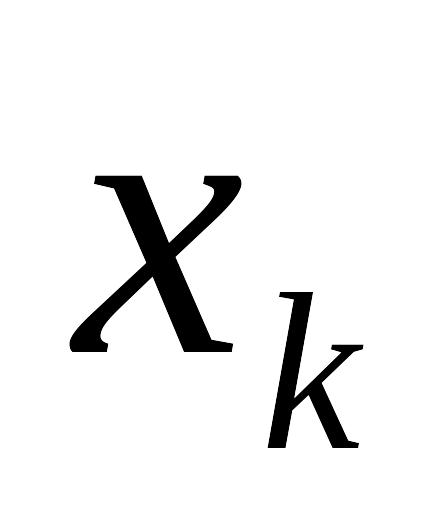
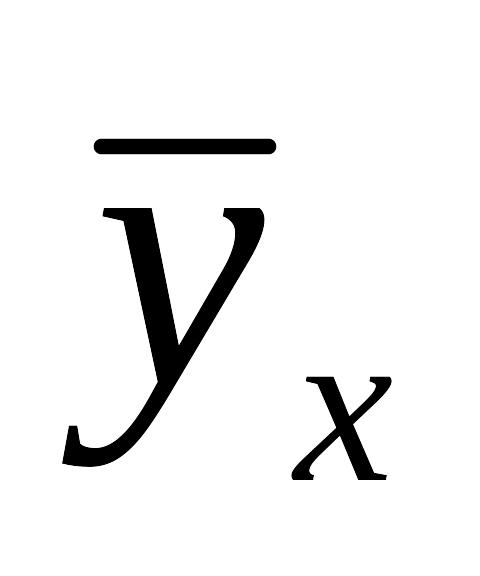
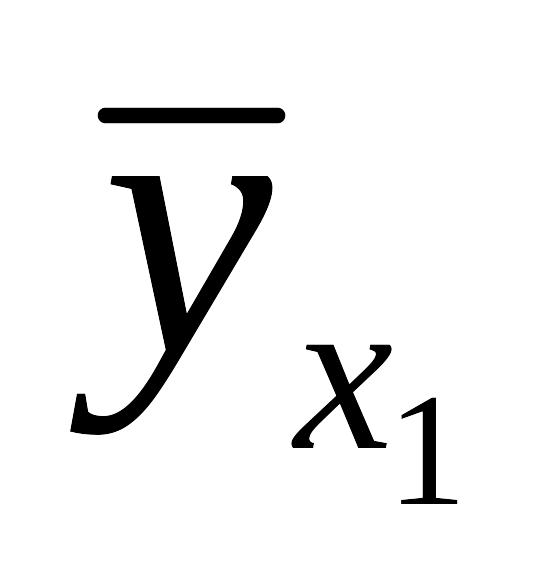
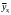
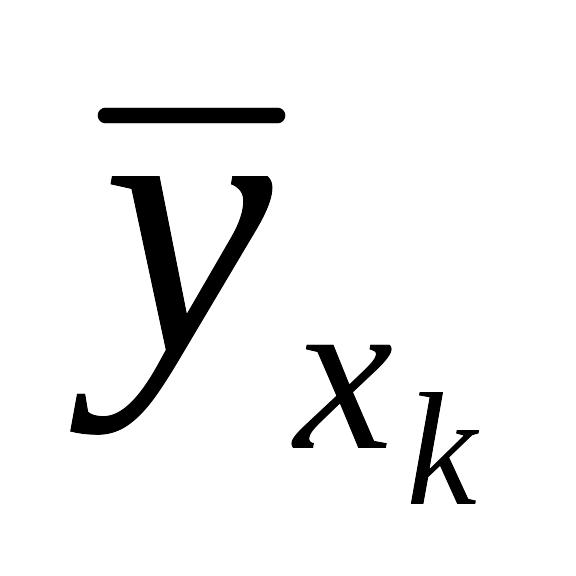
Таблицу 7.4.4 можно рассматривать как зависимость условного среднего значения Y от величины X, т.е. корреляционную зависимость.

Если построить точки ( ) в прямоугольной системе координат, то характер расположения этих точек, построенных по выборочной статистической совокупности, может привести к предположению о форме корреляционной зависимости Y от X.

Действительно, если указанные точки расположены приближенно вдоль прямой линии (рис. 7.4.1), естественно высказать предположение о существовании линейной корреляционной зависимости между изучаемыми величинами. Если же точки расположены приближенно вдоль параболы (рис. 7.4.2) – о квадратичной корреляционной зависимости.

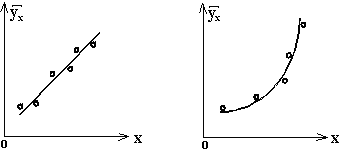
Рис. 7.4.1 Рис. 7.4.2

Аналогично, с помощью корреляционной табл. 7.4.2 для каждого значения можно составить таблицу эмпирического распределение величины X.

Таблица 7.4.5

X			.....		.....
			.....		.....

Условное среднее можно вычислить по формуле:

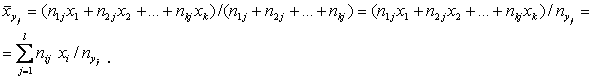
Вычисляя условные средние , составим таблицу, отражающую экспериментальную зависимость условного среднего значения от Y.

Таблица 7.4.6

Y			...		...
			...		...

Построив в прямоугольной системе координат точки , по характеру их расположения можно высказать предположение о форме корреляционной зависимости величины X от Y.

Рассмотрим случай, когда есть основания предполагать наличие линейной корреляционной зависимости между величинами X и Y (в генеральной совокупности их значений), т.е. когда линейные уравнения регрессии имеют вид

, (7.4.1)

. (7.4.2)

В этих случаях для описания корреляционных зависимостей между величинами X и Y по результатам выборочных наблюдений вводят выборочные уравнения линейной регрессии Y на X и X на Y:

, (7.4.3)

, (7.4.4)

где – выборочные коэффициенты линейной регрессии, имеющие смысл выборочных оценок коэффициентов A и C в формулах (7.4.1) и (7.4.2). При этом , являются оценками условных математических ожиданий и , а параметры и – оценками и .