7.3. Интервальные оценки. Доверительный интервал. Нахождение доверительных интервалов для математического ожидания и дисперсии нормального распределения случайной величины

В ряде задач требуется не только найти с помощью статистических данных точечную оценку для параметра распределения, но и оценить ее точность и надежность, так как в силу случайности приближенная замена на может привести к серьезным ошибкам. Для точности оценки в математической статистике используют доверительные интервалы.

Пусть для параметра распределения случайной величины Х получена несмещенная оценка . Задаем достаточно высокую вероятность (например, ) и находим такое значение  > 0, для которого

. (7.3.1)

Равенство (7.3.1) можно переписать в другом виде

. (7.3.2)

Последнее равенство (7.3.2) можно истолковать следующим образом: неизвестное значение параметра а с вероятностью попадает в интервал .

Но так как неизвестное значение параметра является неслучайной величиной, оценка этого параметра – случайной, то равенство (7.3.2) можно истолковать более точно следующим образом: интервал с высокой вероятностью покрывает неизвестный параметр .

Интервал называется доверительным интервалом; центр его находится в точке , радиус его . Вероятность называется доверительной вероятностью или надежностью.

Итак, доверительный интервал – это интервал с центром в точке и радиусом , который с высокой вероятностью (надежностью) покрывает неизвестный параметр . Найти доверительный интервал – это значит по статистическим данным найти центр интервала и радиус его > 0.

1. Доверительный интервал для оценки математического ожидания нормального распределения случайной величины с известным 

Пусть случайная величина X имеет нормальное распределение с неизвестным математическим ожиданием и известной дисперсией ². Пусть произведено n независимых опытов и на основании статистических данных получено выборочное среднее:

Задаем достаточно высокую доверительную вероятность . Требуется построить доверительный интервал . Прежде всего, заметим, что случайная величина также имеет нормальное распределение . Действительно,

;

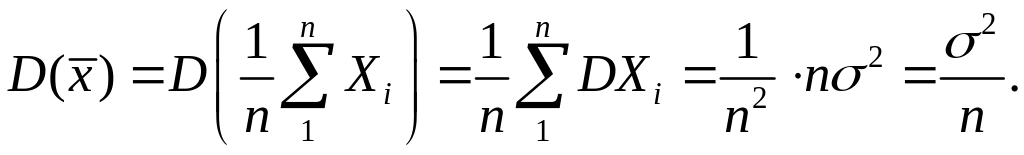
Вероятность попадания случайной величины с нормальным законом распределения в симметричный интервал с центром в точке и радиусом ε равен

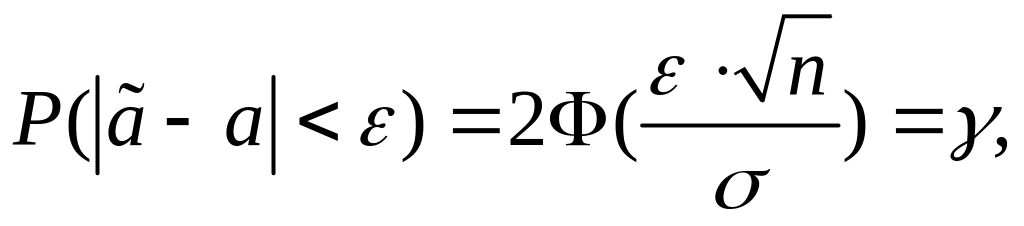(7.3.3)

где – функция Лапласа.

Обозначая , имеем Ф(t) = /2. Затем по табл. 4 приложения находим t по значению Ф(t) = /2; отсюда находится : . Таким образом, доверительный интервал имеет вид

. (7.3.5)

Задача 7.3.1. Случайная величина X имеет нормальное распределение с известным =3. Найти доверительный интервал для оценки неизвестного математического ожидания а по его выборочному среднему , если известны объем выборки и .

Решение. Имеем на основании формулы (7.3.4):

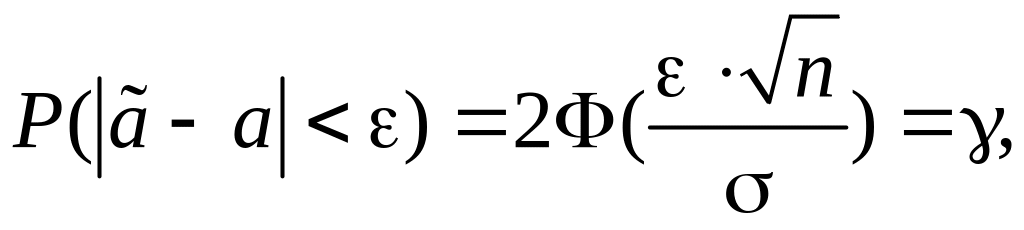t = , .

Из табл. 4 t = 1,96. Тогда . Таким образом,

.

2. Доверительный интервал для оценки математического ожидания нормального распределения с неизвестным 

В отличие от предыдущего, случайная величина X имеет нормальное распределение N (a,) с неизвестным . Пусть произведено n независимых испытаний, построены выборочная средняя и “исправленная” выборочная дисперсия S². Требуется построить доверительный интервал для оценки математического ожидания.

Рассмотрим случайную величину

. (7.3.6)

Распределение (7.3.6) является t – распределение или распределением Стьюдента с степенями свободы.

Действительно, по определению, если – случайная величина с нормальным распределением , а V – случайная величина, распределенная по закону ² с k степенями свободы, то случайная величина распределена по закону Стьюдента с k степенями свободы.

Случайная величина распределена по нормальному закону . Случайная величина

(7.3.7)

распределена также по нормальному закону (как линейная функция относительно нормального аргумента ) с законом .

Известно, что случайная величина

(7.3.8)

распределена по закону ² с степенями свободы. Поэтому случайная величина T распределена по закону Стьюдента.

С ростом степеней свободы распределение Стьюдента приближается к нормальному и уже при практически не отличается от него. Следовательно, при оценке неизвестных параметров по выборке малого объема используют распределение Стьюдента (7.3.6). При построении доверительного интервала для математического ожидания речь идет о вероятности (7.3.1). Имеем

или с учетом (7.3.6)

. (7.3.9)

Обозначая , получаем .

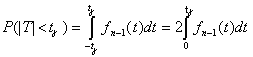Таким образом, имеем

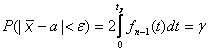. (7.3.10)

Значение определяется по вероятности из табл. 5 приложения распределения Стьюдента. Затем, принимая во внимание, что , находим . Таким образом, доверительный интервал для оценки математического ожидания с неизвестным  имеет вид

. (7.3.11)

Задача 7.3.2. Случайная величина X имеет нормальное распределение. По выборке объемом n = 15 найдены выборочная средняя , “исправленное” среднее квадратическое отклонение . Определить интервальную оценку математического ожидания с доверительной вероятностью .

Решение. По табл. 5 приложения находим . Тогда . По формуле (7.3.11) получим доверительный интервал

.

Замечание. Пусть производится n независимых равноточных измерений некоторой физической величины, истинное значение которой неизвестно и которая имеет нормальное распределение. Пусть – результаты отдельных измерений, рассматриваемые как независимые случайные величины с одним и тем распределением, и имеют одно и то же математическое ожидание (истинное значение измеряемой величины), одинаковые дисперсии ² (измерения равноточные). В этом случае истинное значение измерений физической величины оценивается с помощью среднего выборочного , для которого можно построить доверительный интервал (с неизвестным ) по методу, указанному в п. 2.

Задача 7.3.3. По данным 16-ти независимых равноточных измерений физической величины найдено выборочное среднее и “исправленное” среднее квадратическое отклонение . Требуется оценить истинное значение случайной величины с надежностью .

Решение. Истинное значение измеряемой величины равно ее математическому ожиданию . Поэтому задача сводится к оценке математического ожидания (при неизвестном ) для нормального распределения с помощью доверительного интервала. Доверительный интервал находится с помощью формулы (7.3.11).

Используя табл. 5 приложения по =0,95 и , находим . Имеем

,

.