7.2. Точечные оценки параметров генеральной совокупности по выборочным совокупностям, их свойства. Точечные оценки для математического ожидания и дисперсии случайной величины

Пусть закон распределения случайной величины X содержит неизвестный параметр . Требуется на основании опытных данных найти подходящую оценку для параметра . Пусть

(7.2.1)

наблюдаемые значения случайной величины X, получаемые в результате n независимых опытов. Но, с другой стороны, результат (7.2.1) можно представлять как набор n независимых случайных величин:

, (7.2.2)

представляющих собой n независимых копий случайной величины X, именно – случайная величина, представляющая собой результат i-го опыта, но имеющая тот же закон распределения, что исследуемая случайная величина X.

Случайная величина

, (7.2.3)

построенная на основе статистических данных (7.2.2), называется оценкой (точечной оценкой) параметра . является случайной величиной, закон распределения которой зависит, во-первых, от закона распределения случайной величины X, во-вторых, от числа опытов n. Для того чтобы оценка имела практическую ценность, она должна обладать следующими свойствами:

1. Несмещенность. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру , т.е.

. (7.2.4)

В противном случае (если ) оценка называется смещенной.

Естественно в качестве оценки, т.е. приближенного значения неизвестного параметра, брать несмещенные оценки; в этом случае мы не делаем систематической ошибки в сторону завышения или занижения.

2. Состоятельность. Оценка называется состоятельной, если она сходится по вероятности к оцениваемому параметру a при неограниченном возрастании n:

при . (7.2.5)

Состоятельность оценки означает, что при достаточно большом числе опытов n со сколько угодно большой достоверностью отклонение оценки от истинного значения параметра по модулю меньше любого заранее выбранного числа  > 0.

3. Эффективность. Оценки, обладающие свойством несмещенности и состоятельности, при ограниченном числе опытов могут отличаться дисперсиями. Чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. Поэтому необходимо, чтобы дисперсия оценки была минимальной, т.е. чтобы выполнялось условие:

. (7.2.6)

Оценка, обладающая свойством (7.2.6), называется эффективной, иначе, если при заданном объеме выборки имеет наименьшую дисперсию.

Условия несмещенности, состоятельности и эффективности являются условиями доброкачественности оценки, что является необходимым при обработке статистических данных.

Оценка для математического ожидания случайной величины

Пусть исследуется случайная величина X с математическим ожиданием . Обозначим через x₁, x₂,..., x_n значения случайной величины, полученные в результате n независимых равноточных опытов, т.е. измерений, которые проводились в одинаковых условиях. В качестве оценки для примем среднее арифметическое наблюдаемых значений

. (7.2.7)

в дальнейшем принято называть выборочной средней.

Оценка (7.2.7) является несмещенной, так как .

Оценка (7.2.7) является состоятельной, так как по теореме Чебышева (частный случай) имеем при .

Эффективность оценки (7.2.7) выполняется лишь для узкого класса распределений, в частности, для нормального распределения .

Оценка для дисперсии случайной величины

В качестве оценки для дисперсии рассмотрим следующую величину:

. (7.2.8)

Оценку (7.2.8) принято называть выборочной дисперсией. Проверим ее на состоятельность и несмещенность. Преобразуем выражение (7.2.8) к другому виду:

. (7.2.9)

Первый член в выражении (7.2.9) представляет собой среднее арифметическое n наблюдаемых значений случайной величины X², значит он сходится по вероятности к MX². Второй член сходится по вероятности к . Следовательно, правая часть (7.2.9) сходится по вероятности к величине , что означает, что оценка (7.2.8) состоятельная.

Теперь проверим, является ли выборочная дисперсия несмещенной оценкой:

.

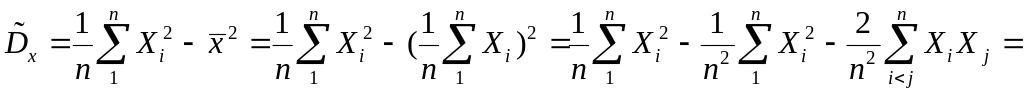
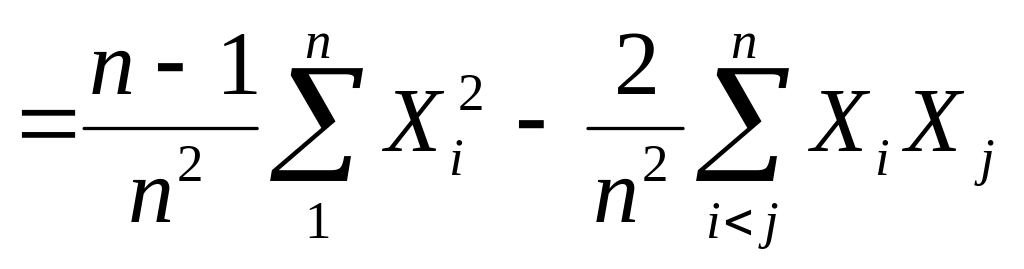Так как дисперсия не зависит от того, в какой точке выбрать начало координат, выберем его в точке ; затем найдем математическое ожидание величины . Имеем .

В силу независимости случайных величин , , и, следовательно,

. (7.2.10)

Очевидно, что выборочная дисперсия является смещенной оценкой. Однако, если умножить величину на , то мы получим для дисперсии оценку, обладающую свойством несмещенности, ибо

.

Эту оценку принято называть «исправленной» выборочной дисперсией и определять формулой

. (7.2.11)

Величину называют «исправленным» средним квадратическим отклонением. Так как множитель стремится к 1 при , то оценка (7.2.11) будет также, как и , состоятельной.

Если имеем интервальное выборочное распределение, нетрудно убедиться, что формулы для выборочной средней (7.2.7), выборочной дисперсии (7.2.8) и «исправленной» выборочной дисперсии (7.2.11) можно переписать в виде

(7.2.12)

(7.2.13)

(7.2.14)

здесь – среднее значение случайной величины X на интервале , т.е. =(x_i-1+x_i)/2.

Задача 7.2.1. Имеется статистический ряд для случайной величины X.

	0-2	2-4	4-6	6-8	8-10
nx	3	4	10	5	3

Найти выборочную среднюю, выборочную дисперсию, «исправленную» выборочную дисперсию, «исправленное» среднее квадратическое отклонение.

Решение. Для удобства вычислений составим таблицу.

		Wi
1	0,12	0,12	-4,08	16,65	1,988
3	0,16	0,48	-2,08	4,33	0,693
5	0,40	2,00	-0,08	0,01	0,04
7	0,20	1,40	1,92	3,69	0,738
9	0,12	1,08	3,92	15,37	1,844
		=5,08

Значения и получены из таблицы с использованием формул (7.2.12), (7.2.13). Имеем .