1.3. Элементы комбинаторики. Некоторые содержательные задачи

Перестановки. Различные представления n элементов называют их перестановками. Число перестановок из n элементов равно произведению всех натуральных чисел от 1 до n:

Р(n)= 1·2·3···n=n! (1.3.1)

При этом полагают 1! = 1,0! = 1. Например, из 5 элементов можно составить 5! = 1· 2· 3· 4· 5 = 120 перестановок, т. е. P(5) = 120 .

Размещения. Пусть имеется множество, содержащее n элементов. Каждое его упорядоченное подмножество, содержащее m элементов, называют размещением из n элементов по m. Размещения из n элементов по m – это все m-элементные подмножества, различающиеся хотя бы одним элементом или порядком их следования. Число размещений из n элементов по m обозначают и вычисляют по формуле

(1.3.2)

или

. (1.3.3)

Формулу (1.3.2) можно обосновать следующим образом. Первый элемент в размещении из n элементов по m можно выбрать n способами, второй (после выбора первого) можно выбрать (n-1) способами, третий – (n-2) способами и т. д., m-й – (n-m+1) способами. Варьируя способы выбора 1-го элемента со способами выбора 2-го, со способами выбора 3-го элемента и т. д. и, наконец, со способами выбора m-го элемента, получим n(n - l) ... (n-m+ 1) способов.

Задача 1.3.1. Каким числом способов можно сдать 4 зачета в 8 дней, если сдавать в 1 день 1 зачет?

Решение. Число способов определяется числом размещений из 8 по 4, т.е.

Сочетания. Пусть имеется множество, состоящее из n элементов. Каждое его подмножество, содержащее m элементов, называется сочетанием из n элементов по m. Все сочетания из n элементов по m – это все m-элементные подмножества, различающиеся друг от друга хотя бы одним элементом; все m-элементные подмножества, отличающиеся друг от друга порядком следования элементов, не считаются различными. Число сочетаний из n элементов по m обозначают и вычисляют по формуле:

(1.3.4)

или

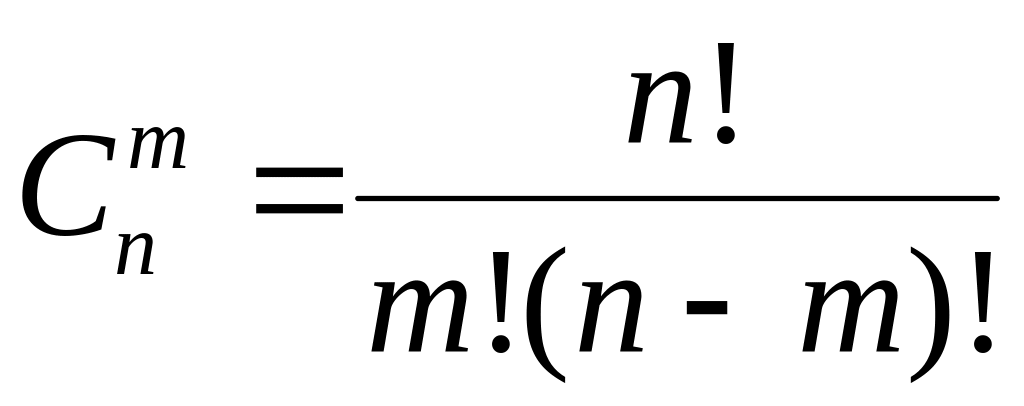. (1.3.5)

Формулу (1.3.4) можно обосновать следующим образом. Из n элементов по m можно составить размещений. Чтобы из размещений получить сочетания из n элементов по m, исключим размещения, отличающиеся друг от друга лишь порядком следования элементов, оставив из них лишь по одному; для этого число разделим на число перестановок из m, т. е. Р(m). Известно также, что .

Задача 1.3.2. Каким числом способов можно выбрать из 10 книг З книги?

Решение. Число способов определяется числом сочетаний из 10 элементов по 3, т.е.

Перестановки с повторениями. Пусть имеется множество, состоящее из n элементов, причем среди них n₁ элементов 1-го типа; n₂ элементов 2-го типа и т.д., n_k элементов k-гo типа, причем n_l+n₂+...+n_k =n. Перестановки из n элементов с повторениями – это всевозможные упорядоченные представления, составленные из данных элементов. Число перестановок с повторениями из n элементов обозначают и вычисляют по формуле

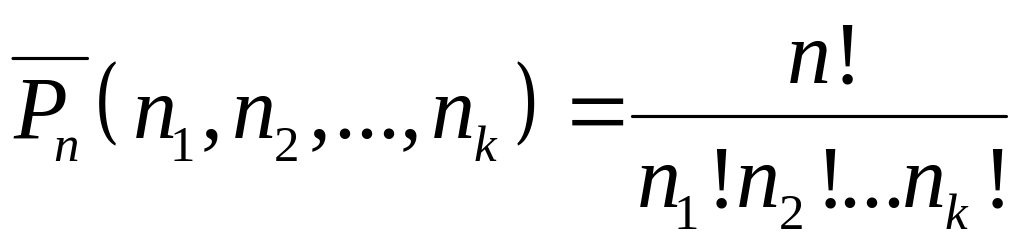. (1.3.6)

Формулу (1.3.6) можно обосновать следующим образом. Если бы все n элементов были различными, число перестановок из них равнялось бы n! Чтобы исключить из них числа перестановок, полученные перестановками одинаковых (одного типа) элементов, оставив лишь по одному их "представителю", разделим на произведение

Задача 1.3.3. Сколько "слов" можно составить путем перестановки букв слова ЭКОНОМИКА?

Решение. В слове n = 9 букв; из них Э – встречается 1 раз, К – 2 раза, О – 2 раза, Η – 1 раз, Μ – 1 раз, И – 1 раз, А – 1 раз. Поэтому число "слов" равно числу перестановок с повторениями из 9 элементов:

.

Сочетания с повторениями. Сочетаниями из n элементов по m с повторениями называются всевозможные m – элементные множества, выбранные из элементов n типов. Число сочетаний с повторениями из n элементов по m обозначают и вычисляют по формуле

. (1.3.7)

Формулу (1.3.7) можно обосновать, сводя задачу о вычислении сочетаний из n по m с повторениями к задаче размещения m одинаковых (неразличимых) шаров по n ячейкам (ящикам): |oo|o|oooo|o|oo|…|oo|.

Здесь m шаров обозначаются кружками; n ящиков ограждены (n+1) перегородками (обозначаются вертикальными палочками). Если две перегородки находятся рядом, это означает, что ящик, определяемый этими перегородками, не содержит шаров. Число размещений m шаров по n ящикам можно свести к числу способов выбора из (m + n – 1) мест (сумма числа шаров и (n–1) внутренних перегородок) (n–1) мест для внутренних перегородок или к числу способов выбора из общего числа (m +n – 1) мест m мест для шаров – .

Задача 1.3.4. Сколько существует костей домино?

Решение. Задача сводится к вычислению числа способов выбора 2 цифр (для одной кости) из цифр 7 типов (0, 1, 2, 3, 4, 5, 6) (допускаются повторения), т. е. вычислению числа сочетаний с повторениями из 7 по 2. Таким образом, число костей домино равно

^.

Размещения с повторениями. Размещениями из n элементов по k называют упорядоченные k-элементные множества, составленные из элементов n типов (допускается наличие в них элементов одного типа, считающихся "одинаковыми"). Число размещений с повторениями из n по k обозначается и вычисляется по формуле

. (1.3.8)

Формулу (1.3.8) можно обосновать следующим образом: 1-й элемент можно выбрать n способами (n типов), 2-й элемент – также n способами и т. д., k-й элемент можно выбрать также n способами. Варьируя способы выбора 1-го элемента со способами выбора 2-го элемента и т. д., получаем формулу (1.3.8).

Задача 1.3.5. Сколько можно составить семизначных телефонных номеров определенного города (считая и номер, состоящий из одних нулей)?

Решение. Каждый телефонный номер содержит 7 цифр (возможны и повторения), выбранных из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Таким образом, к = 7, n = 10, а число телефонных номеров равно числу размещений из 10 по 7 с повторениями, т. е. .

Числа называются также биномиальными коэффициентами, так как они являются коэффициентами в разложении бинома Ньютона, определяющего результат возведения бинома (двучлена) а + b в n-ю степень и имеющего вид

или (1.3.9)

.

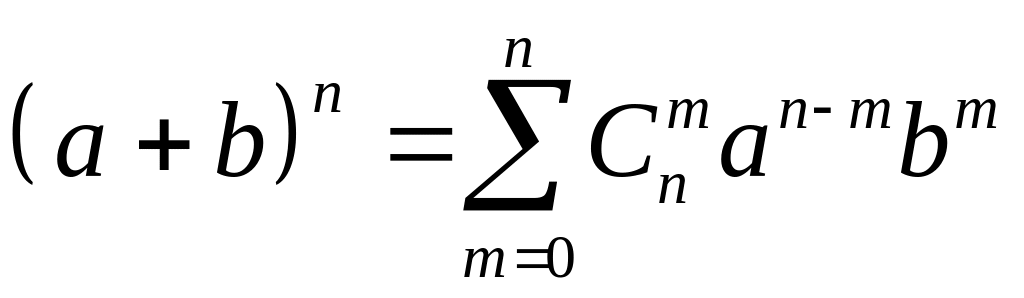Биномиальные коэффициенты, как было указано выше, вычисляются по формуле (1.3.4).

С помощью комбинаторных формул и классического определения вероятности может быть решен ряд содержательных задач. Приведем некоторые из них.

Парадокс Д. Кардано. При бросании двух “правильных” костей подсчитывается сумма выпавших чисел. Как 9, так и 10 можно получить двумя разными способами:

9 = 3 + 6 = 4 + 5 и 10 = 4 + 6 = 5 + 5. Почему тогда 9 появляется чаще, когда бросают две кости, а 10, когда бросают три?

Решение. Необходимо учесть порядок выпадения чисел (в противном случае не все исходы были бы равновозможными). В случае двух костей 9 и 10 могут быть получены соответственно 4 и 3 способами: 9 = 3+6 = 6+3 = 4+5 = 5+4 и 10 = 4+6 = 6+4 = 5+5. Если “выбрасывать” 3 кости, ситуация меняется на противоположную: 9 можно “выбросить” 25 способами, а 10 уже 26 способами.

Задача о днях рождения. Пусть в аудитории находится n студентов. Какова вероятность того, что хотя бы у двух студентов совпадают дни рождения (считать, что в году 365 дней).

Решение. Если n≥366, то очевидно P=1; поэтому рассмотрим случай, когда n≤365. Число комбинаций дней рождения, в которые день рождения не встречается больше одного раза, равно . Число всевозможных случаев определяется числом . Поэтому . Несложно проверить, что если при n=5 P=0,027, то уже при n=60 P=0,994.

Гипергеометрическое распределение. Дана совокупность из n объектов, среди которых k отмеченных (например, бракованных изделий, выигрышных билетов и т.д.). Выбирается наугад n₁≤n объектов. Какова вероятность того, что среди них окажется k₁ отмеченных?

Решение. С помощью классического определения вероятности нетрудно видеть, что , (k₁=0,1,…,min(k,n₁)).

Задача о выигрышах в «Спортлото 6 из 49». Найти вероятность выигрыша на 1 билет на 5 или 6 видов спорта.

Решение. Эта задача является частным случаем предыдущей задачи.

Поэтому . Поэтому , а .