Вопросы для самопроверки

1. Дайте определение случайной функции.

2. Что называют реализацией случайной функции?

3. Чем отличается случайный процесс от случайной функции?

4. Дайте определение математического ожидания случайного процесса.

5. Дайте определение дисперсии случайного процесса.

6. Что называют корреляционной функцией случайного процесса?

7. Какой случайный процесс называют марковским?

8. Что называют цепью Маркова?

9. Что выражает матрица вероятностей перехода цепи Маркова?

10. Напишите формулу Маркова. Что она выражает?

11. Какой случайный процесс называют непрерывной цепью Маркова?

12. Чем различаются цепи Маркова с непрерывным и дискретным временем?

13. Напишите уравнения Колмогорова для вероятностей состояния для непрерывной цепи Маркова.

14. Что называют предельными (финальными) вероятностями? Выпишите уравнения для финальных вероятностей.

15. Какой марковский процесс называют эргодическим?

16. Что называют процессом гибели и размножения? Постройте граф состояний.

17. Напишите формулы для финальных вероятностей процесса гибели и размножения.

18. Что называют простейшим потоком событий?

19. Что называют системой массового обслуживания? Что называют каналами СМО?

20. Дайте определение СМО с отказами и СМО с очередью.

21. Какие параметры характеризуют СМО?

22. Что служит характеристиками эффективности работы СМО?

23. Определите простейшую одноканальную СМО с отказами. Постройте граф состояний.

24. Напишите формулы для вероятностей состояний и характеристик эффективности работы одноканальной СМО с отказами.

25. Определите простейшую многоканальную СМО с отказами. Постройте граф состояний.

26. Напишите формулы Эрланга для вероятностей состояний и формулы для характеристик эффективности работы многоканальной СМО с отказами.

27. Определите простейшую одноканальную СМО с неограниченной очередью. Постройте граф состояний. Напишите формулы для предельных вероятностей состояний и основных характеристик эффективности СМО.

28. Определите простейшую одноканальную СМО с ограниченной очередью. Постройте граф состояний. Напишите формулы для предельных вероятностей состояний и основных характеристик эффективности СМО.

29. Определите простейшую многоканальную СМО с неограниченной очередью. Постройте граф состояний. Напишите формулы для предельных вероятностей состояний и основных характеристик эффективности СМО.

30. Определите простейшую многоканальную СМО с ограниченной очередью. Постройте граф состояний. Напишите формулы для предельных вероятностей состояний и основных характеристик эффективности СМО.

Задачи

1. Случайный процесс определяется формулой X (t)=X cos 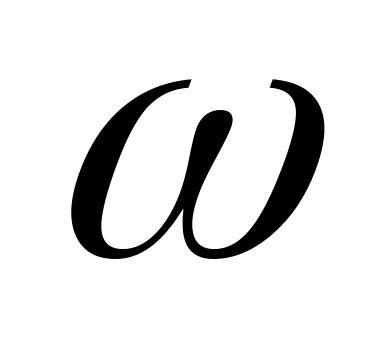t, где X – случайная величина. Найти математическое ожидание, дисперсию и корреляционную функцию этого процесса, если МХ=а, DX= σ ².

Ответ: m_x(t)= acos t; D_x(t)= σ²cos² t;

K_x (t₁, t₂)= σ ² cos t₁ cos t₂.

2. Производится многократное бросание «правильной» монеты. Определяет ли последовательность исходов цепь Маркова? Что изменится при бросаниях «правильной» монеты с вероятностью выпадения герба, равной 2/3?

3. В небольшом городе имеются два рынка – «Дешевый» и «Ближний». Покупатели достаточно лояльно относятся к своим рынкам. Однако каждую неделю 10% покупателей «Дешевого» переходят к «Ближнему» и 20% покупателей «Ближнего» меняют его на «Дешевый». Экономист, занимающийся изучением рыночной конъюнктуры, выбирает случайным образом одного местного жителя и еженедельно опрашивает его, выясняя, в каком рынке он производит свои покупки. Определяет ли данная последовательность исходов (ответов) марковскую цепь?

4. Старый политический принцип гласит, что партия, находясь у власти, имеет более высокие шансы победить на президентских выборах, чем партия оппозиции. Более того, считается, что если партия побеждала на президентских выборах несколько раз подряд, то ее шансы на очередных выборах еще более повышаются. Если такой принцип верен, определяет ли последовательность правящих партий цепь Маркова?

5. Часто кажется, что преуспевающим людям везет. Если, скажем, бизнесмен успешно завершил сделку, вероятность того, что он добьется успеха в следующей сделке, кажется нам выше. Более того, после успешного завершения ряда сделок, вероятность добиться успеха в следующей будет еще более высокой. Если это так, определяет ли такая последовательность исходов (сделок) цепь Маркова.

6. Известно, что заявки по телефону в ателье мод поступают с интенсивностью, равной 90 заявок в час, а средняя продолжительность разговора по телефону 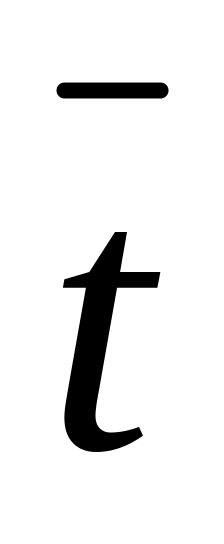_об.=2 мин. Пусть поток заявок является простейшим, а время обслуживания – показательным. При наличии только одного телефонного номера телефонная связь в ателье является одноканальной СМО с отказами. Найти финальные вероятности состояний, а также показатели эффективности работы СМО.

Ответ: p₀=0,25; p₁=0,75; Q=0,25;

P_отк=0,75; A = 22,5 з./ч.

7. Билетная касса с одним окошком представляет собой одноканальную СМО с неограниченной очередью. Касса продает билеты в пункты А и В. Пассажиров, желающих купить билет в пункт А, приходит в среднем трое за 20 мин, в пункт В – двое за 20 мин. Поток пассажиров считается простейшим, время обслуживания – показательным. Кассир в среднем обслуживает трех пассажиров за 10 мин. Найти первые три финальные вероятности состояний СМО, а также ее основные характеристики эффективности.

Ответ: p₀ 0,167; p₁ 0,139;

p₂ 0,116; 4,99; 4,16; 20 мин. 16,7 мин.

8. При условиях задачи 6, определить оптимальное число телефонных номеров в ателье мод, если условием оптимальности считать удовлетворение из каждых 100 заявок на переговоры в среднем не менее 90 заявок.

Указание: для решения задачи сделать расчеты показателей эффективности, постепенно увеличивая число каналов (телефонных номеров), n=2,3,…, добиваясь, чтобы Q=0,9. Ответ: n=5.

9. В юридической консультации прием ведут 3 юриста; в холле имеются три кресла для ожидания приема. Поток клиентов – простейший с интенсивностью 1/2 кл/ч. Время обслуживания – показательное со средним значением 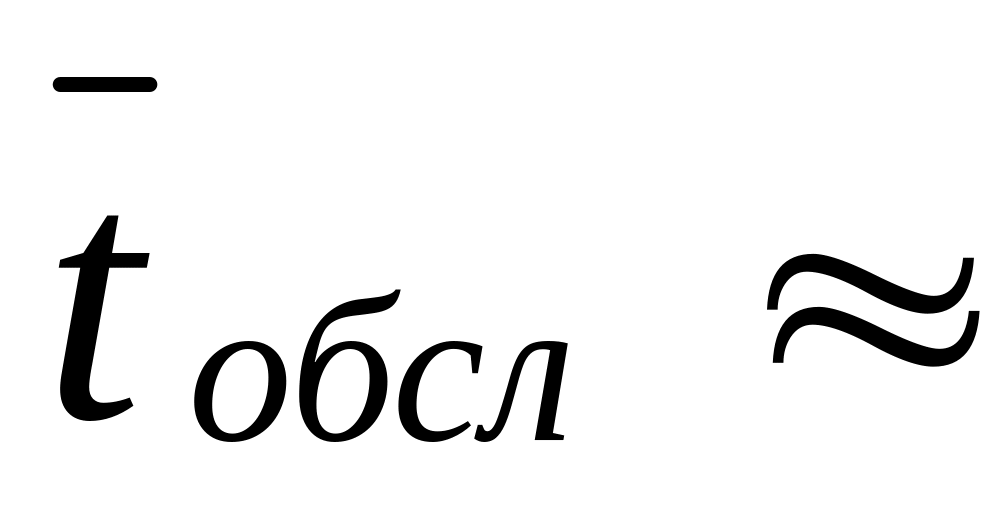20 мин. Если все три кресла в холле ожидания заняты, клиент в очередь не становится. Найти финальные вероятности состояний СМО, а также основные показатели ее эффективности.

Ответ: p₀ 0,012; p₁ 0,049;

p₂ 0,097; p₃ 0,130;

p₄ 0,173; p₅ 0,231;

p₆ 0,307; Q 0,693;

A 8,32; 2,78; 1,56;

4,34; 0,13 ч.; 0,362 ч.

10. Салон одежды с четырьмя кабинами для примерки является многоканальной СМО с неограниченной очередью. В салон прибывает простейший поток покупателей с интенсивностью 45 чел/ч. Время обслуживания (примерки) – показательное; среднее время – 5 мин. Найти основные характеристики эффективности СМО. Что даст увеличение числа кабин для примерки на единицу?

Ответ: а) n=4; p₀ 0,006; 13,01; 16,76; 17,3 мин; 22,3 мин.

б) n=5; p₀ 0,019; 1,38; 5,13; 1,84 мин; 6,84 мин.