
- •Введение
- •1. Случайные события и вероятность
- •1.1. Пространство элементарных событий. Случайные события. Алгебра событий
- •1.2. Классическое определение вероятности. Статистическое определение вероятности
- •1.3. Элементы комбинаторики. Некоторые содержательные задачи
- •1.4. Аксиоматическое введение вероятности
- •1.5. Теоремы о вероятностях случайных событий
- •1.6. Формула полной вероятности и формула Байеса
- •1.7. Геометрические вероятности
- •1.8. Схема независимых испытаний Бернулли. Формула Бернулли. Формула Пуассона. Локальная и интегральная теоремы Муавра-Лапласа
- •Вопросы для самопроверки
- •2. Случайные величины
- •2.1. Случайные величины. Случайные величины дискретного типа. Ряд распределения. Функция распределения
- •2.2. Случайная величина непрерывного типа. Плотность вероятности распределения случайной величины
- •2.3. Числовые характеристики случайной величины. Математическое ожидание и дисперсия, их свойства
- •2.4. Пуассоновский поток событий
- •Вопросы для самопроверки
- •3. Системы случайных величин
- •3.1. Закон распределения системы двух случайных величин. Функция распределения, плотность распределения системы двух случайных величин
- •3.2. Условные законы распределения. Зависимые и независимые случайные величины
- •3.3. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции
- •Вопросы для самопроверки
- •4. Функции случайных величин
- •4.1. Преобразование случайных величин (случай двух переменных)
- •4.2. Распределение суммы, разности, произведения и частного двух случайных величин
- •4.3. Преобразование случайных величин (случай одной переменной)
- •4.5. Распределение Стьюдента
- •Вопросы для самопроверки
- •5. Закон больших чисел
- •5.1. Неравенства Чебышева
- •5.2. Теорема Чебышева
- •5.3. Теорема Бернулли
- •5.4. Центральная предельная теорема
- •Вопросы для самопроверки
- •6. Случайные процессы. Марковские случайные процессы. Системы массового обслуживания
- •6.1. Случайные процессы
- •6.2. Марковские случайные процессы. Марковские цепи
- •6.3. Марковские процессы с дискретными состояниями и непрерывным временем. Уравнения Колмогорова
- •6.4. Процессы гибели и размножения
- •6.5. Потоки случайных событий
- •6.6. Приложения марковских процессов
- •6.7. Системы массового обслуживания
- •6.8. Системы массового обслуживания с отказами Одноканальная смо с отказами
- •6.9. Системы массового обслуживания с очередями
- •Вопросы для самопроверки
- •7. Математическая статистика
- •7.1. Генеральная совокупность и выборка. Статистический ряд. Статистическая функция распределения. Гистограмма
- •7.2. Точечные оценки параметров генеральной совокупности по выборочным совокупностям, их свойства. Точечные оценки для математического ожидания и дисперсии случайной величины
- •7.3. Интервальные оценки. Доверительный интервал. Нахождение доверительных интервалов для математического ожидания и дисперсии нормального распределения случайной величины
- •1. Доверительный интервал для оценки математического ожидания нормального распределения случайной величины с известным
- •2. Доверительный интервал для оценки математического ожидания нормального распределения с неизвестным
- •3. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения
- •7.4. Построение прямых линий регрессии по выборочным данным
- •1. Нахождение параметров выборочных уравнений прямой линии регрессии по несгруппированным данным
- •2. Нахождение параметров выборочных уравнений прямой линии регрессии по сгруппированным данным
- •7.5. Нахождение оценки для коэффициента корреляции двух случайных величин
- •7.6. Статистическая проверка гипотез. Статистическая гипотеза. Нулевая и конкурирующая гипотеза. Статистический критерий. Критическая область
- •7.7. Проверка гипотезы о значимости выборочного коэффициента корреляции
- •7.8. Проверка гипотезы о распределении генеральной совокупности. Критерий 2 Пирсона
- •7.10. Сравнение генеральных средних двух нормально распределенных случайных величин (малые независимые выборки)
- •7.11. Сравнение двух дисперсий нормальных генеральных совокупностей
- •7.12. Сравнение наблюдаемой относительной частоты с гипотетической вероятностью наступления события
- •Вопросы для самопроверки
- •8. Варианты контрольной paбoты № 1 по теории вероятностей вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •9. Варианты контрольной работы № 2 по случайным процессам и математической статистике вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Приложение
- •Суммарные вероятности для распределения Пуассона
- •Критические точки распределения Стьюдента
- •Библиографический список
6.8. Системы массового обслуживания с отказами Одноканальная смо с отказами
Пусть
СМО имеет один канал, на который поступает
поток заявок с интенсивностью λ.
Поток обслуживания имеет интенсивность
μ (среднее время обслуживания
![]() ).
).
СМО имеет два состояния: s0 – канал свободен; s1 – канал занят. Граф состояний имеет простой вид (рис. 6.8.1).
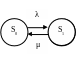
Рис. 6.8.1
Уравнения для предельных вероятностей состояний имеют вид
λp0 = μp1 ; μp1 = λp0, (6.8.1)
которые вырождаются в одно уравнение; решая его вместе с нормированным уравнением
p0 + p1 = 1,
получим для предельных вероятностей
![]() ;
;
![]() . (6.8.2)
. (6.8.2)
p0 представляет собой среднее относительное время пребывания СМО в состоянии s0; p1 - среднее относительное время пребывания СМО в состоянии s1.
Несложно
подсчитать основные характеристики
эффективности СМО. Относительная
пропускная способность СМО вычисляется
по формуле
![]() ;
вероятность отказа
;
вероятность отказа
![]() ;
абсолютная пропускная способность СМО
;
абсолютная пропускная способность СМО
![]() .
.
Многоканальная СМО с отказами
Пусть СМО имеет n каналов, на которые поступает поток заявок с интенсивностью λ. Поток обслуживания любого из n каналов имеет интенсивность μ. Найдем предельные вероятности состояний и основные характеристики работы СМО. СМО в этом случае имеет следующие состояния: s0 - СМО свободна; s1 – занят один канал, остальные свободны; ...; sk - заняты k каналов, остальные свободны; ...; sn - заняты все n каналов.
Граф состояний СМО имеет следующий вид
λ
nμ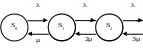




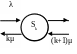 …
…
Рис. 6.8.2
Финальные вероятности состояний СМО вычисляются с помощью аналогичных формул схемы размножения и гибели :
![]()
![]() …;
…;
![]() …;
…;
![]() (6.8.3)
(6.8.3)
![]()
Введем
параметр
![]() ,
называемый приведенной
интенсивностью потока заявок, иначе,
интенсивностью нагрузки канала.
Тогда формулы (6.8.3) можно переписать в
более удобной форме:
,
называемый приведенной
интенсивностью потока заявок, иначе,
интенсивностью нагрузки канала.
Тогда формулы (6.8.3) можно переписать в
более удобной форме:
![]()
![]()
![]() …;
…;![]() (6.8.4)
(6.8.4)
Формулы (6.8.4) называют формулами Эрланга. Характеристики эффективности работы СМО:
1)
вероятность отказа
![]()
2)
относительная пропускная способность
СМО
![]()
3)
абсолютная пропускная способность СМО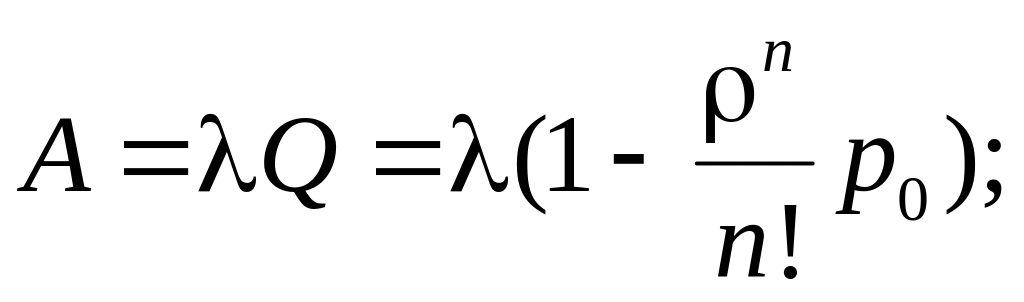
4)
среднее число занятых каналов
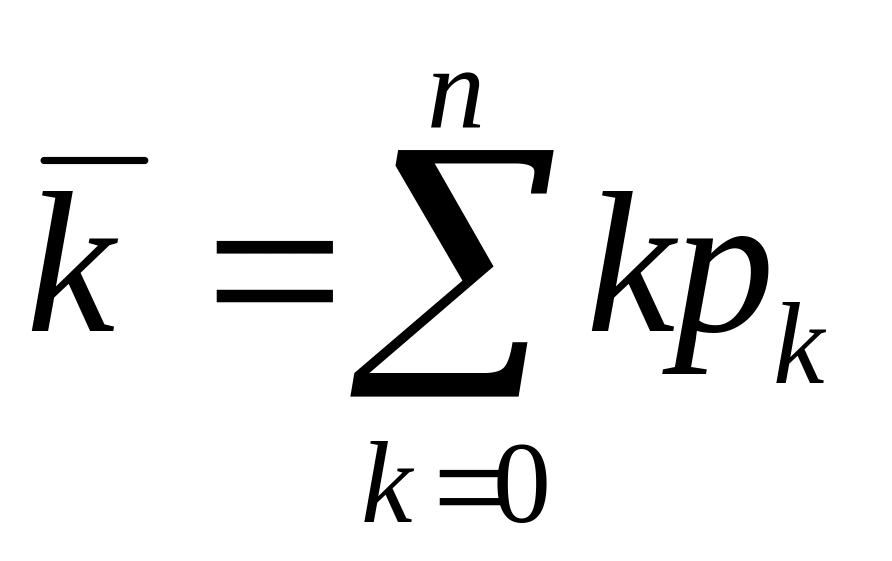 или
или
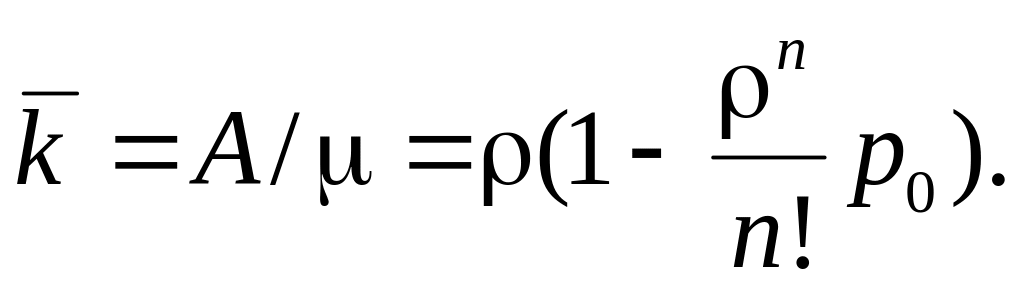
6.9. Системы массового обслуживания с очередями
Одноканальные системы массового облуживания с неограниченной очередью
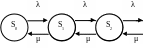
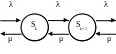
Пусть на одноканальную СМО поступает простейший поток заявок с интенсивностью λ, а время обслуживания - показательное с интенсивностью μ. Пусть теперь заявки в случае, если канал обслуживания занят, не получают отказ, а становится в очередь, причем длина очереди неограничена. Считая процесс обслуживания марковским процессом, сформируем состояния системы следующим образом: s0 – СМО свободна; s1 – канал занят, очереди нет; s2 – канал занят, одна заявка стоит в очереди; … ; sk – канал занят, (k-1) заявок стоит в очереди; … Граф состояний системы представлен на рис. 6.9.1.
 …
… …
…
Рис. 6.9.1
Система уравнений для предельных вероятностей состояний полученная из соответствующих уравнений Колмогорова, имеет вид :
λp0 = μp1; (λ + )p1 = p0 + р2; … ; (λ + )pk = рk-1 + μpk+1; …
Из
этой системы уравнений при условиях
![]() и
и
![]() имеем следующие формулы для финальных
вероятностей
имеем следующие формулы для финальных
вероятностей
p0 =1-ρ; pk = ρk(1 – ρ), k = 1,2,… (6.9.1)
Для характеристик эффективности СМО имеем следующие формулы:
A=λ;
Q=1;
Pотк=0;
![]() =ρ/(1-ρ);
=ρ/(1-ρ);
![]() =ρ2/(1-ρ);
=ρ2/(1-ρ);
![]() сист=
ρ/λ(1-ρ);
ог=
ρ2/λ(1-ρ);
сист=
ρ/λ(1-ρ);
ог=
ρ2/λ(1-ρ);
![]() =λ/μ=ρ.
=λ/μ=ρ.
Здесь
–
среднее число заявок в СМО;
![]() –
среднее число заявок в очереди.
–
среднее число заявок в очереди.
Одноканальные системы массового обслуживания с ограниченной очередью
Пусть
на одноканальную СМО поступает простейший
поток заявок с интенсивностью λ, время
обслуживания – показательное с
интенсивностью μ=1/![]() обс.
обс.
Пусть теперь очередь имеет ограниченную длину и состоит из m мест. Если заявка приходит в момент, когда все эти места заняты, она получает отказ и покидает СМО.
Сформируем состояния следующим образом: s0 – СМО свободна; s1 – канал занят, одна заявка стоит в очереди; …; sk – канал занят, k-1 заявок стоят в очереди; …; sm+1 – канал занят, m заявок стоит в очереди. Граф состояний системы представлен на рис. 6.9.2.
λ
λ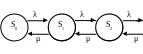
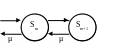
Рис. 6.9.2
Система уравнений для предельных вероятностей системы, полученная из соответствующих уравнений Колмогорова, имеет вид:
λp0 = μp1; (λ + )p1 = p0 + μp2; … ; λpm = μpm+1.
Из
этой системы
уравнений при условии
![]() и любом ρ = λ/μ имеем следующие формулы
:
и любом ρ = λ/μ имеем следующие формулы
:
p0 = (1-ρ) / ( 1-ρm+2 ) ; pk = ρk p0 , k = 1, 2, … , m+1; (6.9.3)
Для показателей эффективности системы имеем следующие формулы:
A
= λ(1-pm+1)
; Q = 1-pm+1
;
Pотк
= pm+1
.
![]() = 1 – p0
;
= 1 – p0
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() . (6.9.4)
. (6.9.4)
Задача
6.9.1. В клинике
прием больных обеспечивает один врач
; в салоне ожидания приема 3 кресла. Пусть
поток клиентов простейший с интенсивностью
λ=2 кл./ч. Время обслуживания (приема
клиента) – показательное со средним
значением
![]() мин. Если все три кресла в салоне ожидания
заняты, клиент в очередь не становится.
Считая процесс марковским, сформировать
состояния системы, построить граф
состояний системы. Найти предельные
вероятности системы, а также показатели
ее эффективности .
мин. Если все три кресла в салоне ожидания
заняты, клиент в очередь не становится.
Считая процесс марковским, сформировать
состояния системы, построить граф
состояний системы. Найти предельные
вероятности системы, а также показатели
ее эффективности .
Решение. Пусть s0 – СМО свободна; s1 – врач занят, очереди нет; s2 – врач занят, в очереди один больной; s3 – врач занят, в очереди 2 больных ; s4 – врач занят, в очереди 3 больных; λ=2 кл./ч., μ=3 кл./ч.
Граф состояний системы имеет следующий вид:
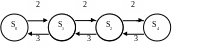
Рис. 6.9.3
Предельные вероятности определяются по формулам (6.9.3) при ρ = 2/3. Имеем p0 0,384 ; p1 0,256 ; p2 0,170 ; p3 0,114 ; p4 0,076. Это означает, что более трети времени (38,4%) врач свободен.
Средняя доля обслуживаемых клиентов Q=1-Pотк = 1-p4 = 1-0,076 = 0,924.
Среднее
число клиентов обслуживаемых врачом
за час, равно A=
λQ=2·0,924=1,848.
Среднее число клиентов в очереди
![]() 0,209.
Среднее число занятых клиентов
(вероятность того, что канал занят)
0,209.
Среднее число занятых клиентов
(вероятность того, что канал занят)
![]() =
1-p0
0,616.
Среднее число клиентов в клинике
=
+
0,825.
Среднее время пребывания клиента в
системе клиники
=
1-p0
0,616.
Среднее число клиентов в клинике
=
+
0,825.
Среднее время пребывания клиента в
системе клиники
![]() /λ
0,413
ч.
/λ
0,413
ч.
Простейшая многоканальная СМО с неограниченной очередью
Пусть
имеем n-канальную
СМО, на которую поступает простейший
поток заявок с интенсивностью λ; время
обслуживания – показательное с параметром
μ = 1/![]() .
Если заявка поступает в момент времени,
когда все каналы заняты, заявка становится
в очередь, длина которой неограничена.
Сформируем состояния СМО: s0
– СМО свободна; s1
– занят один канал, очереди нет; …; sk
– занято k
каналов, очереди нет; …; sn
– заняты все n
каналов, очереди нет; …; sn+1
– заняты все n
каналов, одна заявка стоит в очереди;
sn+r
– заняты все n
каналов, r
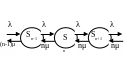
заявок стоит в очереди и.т.д. Граф
состояний СМО имеет следующий вид:
.
Если заявка поступает в момент времени,
когда все каналы заняты, заявка становится
в очередь, длина которой неограничена.
Сформируем состояния СМО: s0
– СМО свободна; s1
– занят один канал, очереди нет; …; sk
– занято k
каналов, очереди нет; …; sn
– заняты все n
каналов, очереди нет; …; sn+1
– заняты все n
каналов, одна заявка стоит в очереди;
sn+r
– заняты все n
каналов, r
заявок стоит в очереди и.т.д. Граф
состояний СМО имеет следующий вид:
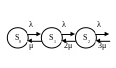 …
…
 …
…
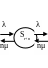 …
…
Рис. 6.9.4
Система уравнений для предельных вероятностей состояний, получаемая из соответствующих состояний Колмогорова, имеет вид
λp0 = μp1; (λ+μ) p1 = λp0 + 2μp2; (λ+2μ) p2 = λp1+ 3μp3; …; (λ+nμ) pn = λpn-1 + nμpn+1;
(λ+nμ) pn+1 = λpn + nμpn+r; …; (λ+nμ) pn+r = λpn+r-1 + nμpn+r-1, …
Из последней системы алгебраических уравнений получим формулы для финальных вероятностей состояний:
p0=(1+ ρ + ρ2/2! + … + ρn/n! + ρn+1/(n n! (1-æ)))-1, ρ = λ/μ, æ = ρ/n < 1;
![]() ,
(1
k
n);
,
(1
k
n);
![]() (r
1). (6.9.5)
(r
1). (6.9.5)
Для характеристик эффективности имеем следующие формулы:
![]() ;
;
![]() =
+
=
+![]() =
+ρ;
=
+ρ;
![]() /λ;
оч
=
/λ.
(6.9.6)
/λ;
оч
=
/λ.
(6.9.6)
Простейшая многоканальная СМО с ограниченной очередью
Пусть,
как и в предыдущем случае, имеем
n-канальную
СМО, на которую поступает простейший
поток заявок с интенсивностью λ;
время обслуживания – показательное с
параметрами
![]() .
Но в отличие от предыдущего, если все n
каналов заняты, заявка становится в
очередь, длина которой ограничена и
имеет m
мест.
.
Но в отличие от предыдущего, если все n
каналов заняты, заявка становится в
очередь, длина которой ограничена и
имеет m
мест.
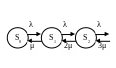
Сформируем состояния СМО: s0 – СМО свободна; s1 – занят один канал, очереди нет; …; sn – заняты n каналов, очереди нет, sn+1 – заняты n каналов, одна заявка в очереди; …; sn+m – заняты n каналов, m заявок в очереди.
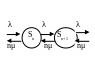
Граф состояний имеет следующий вид:
 …
… …
…
Рис. 6.9.5
Система уравнений для предельных вероятностей состояний, полученная из соответствующих уравнений Колмогорова, имеет вид:
λp0 = µp1; (λ+µ) p1 = λp0 + 2µp2; …; (λ+nµ) pn = λpn-1 + nµpn+1; …; nµpn+m = λpn+m-1.
Из последней системы алгебраических уравнений получим формулы для финальных вероятностей состояний:
p0
= (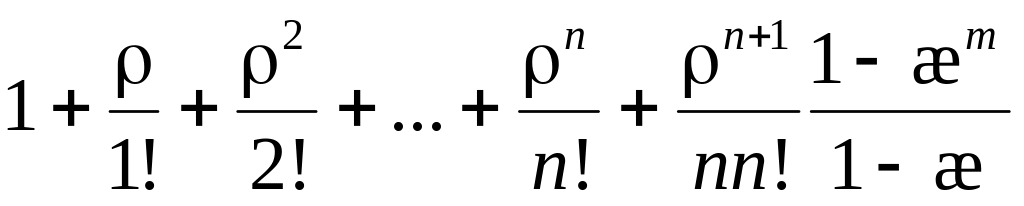 )-1;
pk
=
)-1;
pk
=![]() (1
k
n);
pn+r
=
(1
k
n);
pn+r
=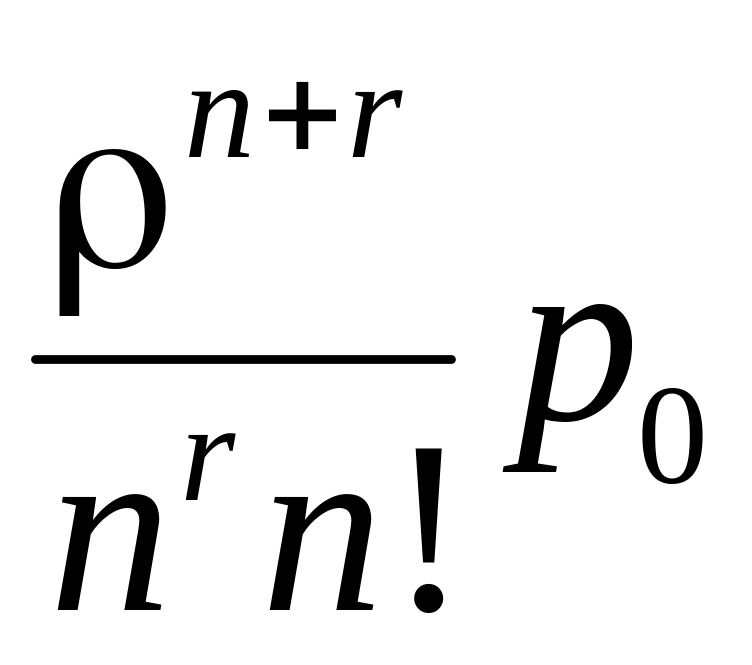 (1
r
m),
(1
r
m),
где æ =
![]() /
n = λ/(nµ). (6.9.7)
/
n = λ/(nµ). (6.9.7)
Для характеристик эффективности СМО имеем
A=λ(1-pn+m);
Q=1-pn+m;
Pотк
= pm+n;
=
(1-pn+m);
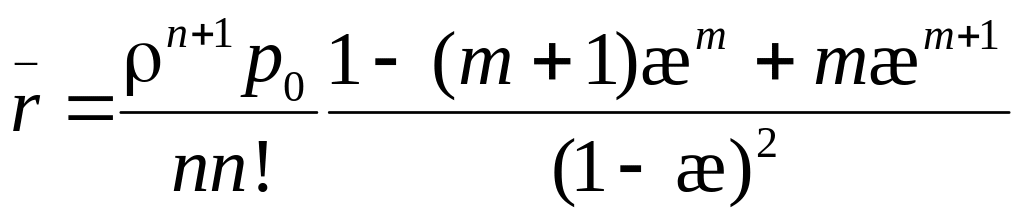 ;
;
![]() ;
;
![]() ;
;
![]() . (6.9.8)
. (6.9.8)
Задача 6.9.2. СМО, описанная в задаче 6.9.1, претерпела изменения в связи с эпидемией гриппа. В связи с увеличением в два раза интенсивности потока больных, администрация решила увеличить в два раза число обслуживаемых врачей и число кресел для ожидания без уменьшения среднего времени обслуживания. По-прежнему считаем, что если все кресла в зале ожидания заняты, клиент в очередь не становится. Как изменятся показатели эффективности СМО?
Решение. В данном случае СМО имеет два канала обслуживания; λ=4 кл/ч; µ=3 кл/ч; m=6. Пусть s0 – СМО свободна; s1 – один врач занят, очереди нет; s2 – оба врача заняты, очереди нет; s3 – оба врача заняты, один больной в очереди; s4 – оба врача заняты, два больных в очереди; s5 – оба врача заняты, три больных в очереди; s6 – оба врача заняты, четыре больных в очереди; s7 – оба врача заняты, пять больных в очереди; s8 – оба врача заняты, шесть больных в очереди. Граф состояний имеет следующий вид:

Рис. 6.9.6
С помощью формул (6.9.7) получим значение предельных вероятностей состояний:
p0 0,206; p1 0,275; p2 0,183; p3 0,122; p4 0,081; p5 0,054; p6 0,037; p7 0,025; p8 0,017.
Из этого следует, что 20,6% врачи клиники свободны.
Вероятность
отказа для пришедшего в клинику больного
определяется величиной Pотк
=p8=0,017.
Средняя доля обслуживаемых клиникой
больных определяется величиной
Q=1-p8
0,983;
среднее число больных, обслуживаемых
клиникой за один час A=λQ
3,932;
среднее число занятых каналов (врачей)
![]() 1,311;
среднее число больных в очереди
1,311;
среднее число больных в очереди
![]() 1,067;
среднее число больных в клинике (за 1
час)
1,067;
среднее число больных в клинике (за 1
час)
![]() 2,378;
среднее время пребывания больного в
клинике равно
0,59
ч.
2,378;
среднее время пребывания больного в
клинике равно
0,59
ч.
