6.3. Марковские процессы с дискретными состояниями и непрерывным временем. Уравнения Колмогорова

Пусть переход системы из одного состояния в другое может происходить в любой случайный момент времени. Марковский случайный процесс с дискретными состояниями и непрерывным временем часто называют непрерывной цепью Маркова. В этом случае не имеет смысла говорить о вероятностях перехода из одного состояния в другое, т.к. для любого момента времени t p_ij(t)=0. Вместо неё вводят плотность вероятности перехода из i-го в j-е состояние по формуле

Плотность вероятности перехода может быть как постоянной (λ_ij=const), так и зависящей от времени (λ_ij = λ_ij(t)). В первом случае непрерывную цепь Маркова называют однородной, во втором - неоднородной. Простейшим примером однородной непрерывной цепи Маркова является случайный процесс X(t), представляющий собой число наступлений события А (успеха) до момента времени t в простейшем (пуассоновском) потоке событий.

При рассмотрении непрерывных цепей Маркова удобно представлять переходы системы из состояния в состояние как происходящие под влиянием потоков событий; при этом плотность вероятности перехода приобретает смысл интенсивностей λ_ij соответствующих потоков событий. Потоком вероятности перехода из состояния s_i в состояние s_j называется величина λ_ij p_i(t).

Для описания непрерывной цепи Маркова введем вероятности состояний

p₁(t), p₂(t), …,p_n(t), (6.3.2)

где p_i(t) вероятность того, что система в момент времени t находится в состоянии s_i. Очевидно, что в любой момент времени

. (6.3.3)

Для нахождения вероятностей состояния нужно решить систему дифференциальных уравнений (уравнений Колмогорова), имеющих вид:

, i = 1, 2, 3, …, n. (6.3.4)

В уравнениях (6.3.4) интенсивности потоков могут зависеть от времени t.

Уравнения Колмогорова (6.3.4) можно составить, пользуюсь размеченным графом состояний и следующим мнемоническим правилом: производная вероятности каждого состояния равна сумме всех потоков вероятности, входящих в данное из других состояний, минус сумма всех выходящих из данного состояния потоков.

Пример 6.3.1. Пусть граф состояний непрерывной цепи Маркова имеет вид

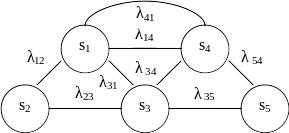
Рис. 6.3.1.

Составить уравнения Колмогорова.

Решение. Пользуясь вышеуказанным правилом, имеем

;

;

;

;

.

Часто возникает вопрос о предельном поведении вероятностей p_i(t) при t  ∞. В некоторых случаях существуют предельные (финальные) вероятности. Это означает, что со временем устанавливается стационарный режим, в ходе которого система переходит из одного состояния в другое, но вероятности состояний уже не меняются. Финальные вероятности могут быть интерпретированы как среднее относительное время пребывания системы в данном состоянии. В этом случае непрерывная цепь Маркова называется эргодической.

По графу состояний можно определить, существует финальные состояния или нет. Для этого вводятся существенные и несущественные состояния. Впервые такая классификация состояний для цепей Маркова была введена российским математиком А.Н. Колмогоровым.

Состояние s_i называется несущественным, если существуют такое состояние s_j и такое n, что p_ij(n) > 0, но p_ji(m) = 0 для всех m. Иными словами, несущественное состояние обладает тем свойством, что из него можно с положительной вероятностью попасть в некоторое другое состояние, но из этого другого состояния вновь вернуться в первоначальное (несущественное) состояние уже нельзя.

Все состояния, отличные от несущественных, называются существенными. Пусть s_i и s_j являются существенными и существуют такие натуральные m и n, что наряду с неравенством p_ij(m) > 0 выполняется неравенство p_ji(n) > 0; в этом случае они называются сообщающимися. Очевидно, что если s_i сообщается с s_j, а s_j сообщается s_k, то s_i сообщается с s_k. Таким образом, все существенные состояния разбиваются на классы ; все существенные состояния , принадлежащие одному классу, сообщаются, а принадлежащие разным классам – не сообщаются между собой. Если все состояния системы существенные, они образуют единственный класс.

Состояние s_i называют поглощающим, если p_ii = 1. Если для марковской цепи существует хотя бы одно поглощающее состояние и из любого не поглощающего состояния можно перейти в какое-нибудь поглощающее, цепь Маркова называют поглощающей.

Имеет место следующий результат:

Теорема 6.3.1. Для того, чтобы при конечном числе состояний для непрерывной цепи Маркова существовали предельные вероятности состояний, необходимо и достаточно, чтобы из каждого существенного состояния можно было перейти (за какое-нибудь определенное число шагов) в другое существенное состояние.

Из несущественных состояний система рано или поздно уйдет в одно из существенных состояний и больше в них не вернется. Финальные вероятности для них равны нулю.

Приведем также достаточное условие существования предельных вероятностей.

Теорема 6.3.2. Для существования предельных вероятностей достаточно, чтобы из любого состояния системы можно было (за определенное число шагов) перейти в любое другое.

Финальные вероятности могут быть получены из уравнений Колмогорова, если положить в них производные по времени равными нулю. В этом случае уравнения (6.3.4) можно записать в следующем виде:

, i = 1,2, …, n. (6.3.5)

Систему линейных алгебраических уравнений (6.3.5), из которых определяются финальные вероятности, можно составить непосредственно, руководствуясь следующим правилом: для каждого состояния суммарный входящий поток равен суммарному выходящему. Чтобы получить единственное решение системы (6.3.5), к ним следует добавить нормированное условие (6.3.3).