6.2. Марковские случайные процессы. Марковские цепи

Рассмотрим частный случай случайных процессов – марковские случайные процессы. Такие процессы называют марковскими, потому что они впервые были систематически изучены известным российским математиком А.А. Марковым в начале XX века.

Определение 6.2.1. Случайный процесс X(t) называется марковским, если для любых n моментов времени t₁< t₂< ... < t_n условная функция распределения последнего значения X(t_n) при фиксированных значениях X(t₁), ... , X(t_n-1) в моменты времени t₁,…,t_n-1 зависит лишь от значения X(t_n-1) в непосредственно предшествующий ему момент времени t_n-1 и не зависит от его значений в более ранние моменты времени t₁, …, t_n-2. Это свойство марковского процесса называют свойством отсутствия последействия.

Значения случайного процесса удобно отождествлять с состояниями системы, которую описывает данный случайный процесс. При этом переход системы из одного состояния в другое происходит в фиксированные или случайные моменты времени. Поэтому в терминах состояний особенность марковского случайного процесса состоит в том, что вероятность состояния системы в момент времени t_n зависит лишь от того, в каком состоянии находилась система в непосредственно предшествующий ему момент времени t_n-1, и не зависит от того, в каких состояниях находилась система в более ранние моменты времени t₁,...,t_n-₂.

Укажем еще одно общее и важное свойство марковских процессов: для них эволюция вероятности перехода из одного состояния в другое описывается дифференциальным уравнением вида

, (6.2.1)

где А - некоторая квадратная матрица.

Это свойство позволяет исследовать поведение марковских процессов при помощи хорошо разработанных методов решения соответствующих дифференциальных уравнений.

В зависимости от того, дискретным или непрерывным являются множество состояний и множество значений аргумента t, различают основные виды марковских случайных процессов.

В случае дискретного множества состояний марковский случайный процесс называется марковской цепью.

Цепь Маркова представляет собой последовательность испытаний, в каждом из которых система принимает одно и только одно из n состояний полной группы s₁,s₂, …, s_n (или, иначе, состояния 1,2,.. .,n ). При этом вероятность p_ij(k) того, что после k-го испытания система будет находиться в состоянии j, при условии, что после (k-l)-гo испытания она находилась в состоянии i, не зависит от результатов остальных, ранее произведенных испытаний.

Различают марковские цепи с дискретным временем, если изменение состояний происходит в определенный фиксированный момент времени, и марковские цепи с непрерывным временем, если изменение состояний происходит в любые случайные моменты времени.

Цепь Маркова называют однородной, если условная вероятность р_ij(k) не зависит от номера испытания; в этом случае вместо нее пишут р_ij и называют ее переходной вероятностью. Все переходные вероятности могут быть представлены матрицей перехода системы, имеющей следующий вид:

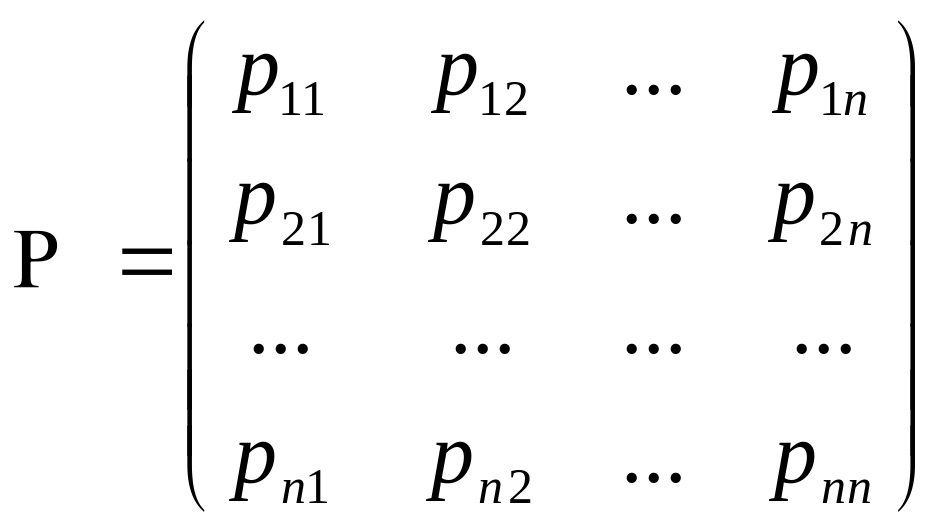. (6.2.2)

Так как в любой строке матрицы помещены вероятности перехода из одного состояния i в любое возможное состояние j, сумма переходных вероятностей каждой строки матрицы перехода равна 1, т.е. (i = 1,2, …,n).

Пусть Р_ij(m) - вероятность того, что в результате m испытаний (шагов) система перейдет из состояния i в состояние j (если m=1, то P_ij(1) = p_ij). По формуле полной вероятности (с использованием вероятностей перехода в промежуточное состояние P_ij(m) имеем формулу:

. (6.2.3)

Формулу (6.2.3) называют формулой Маркова.

Если положить m=2, k=l, формула (6.2.3) превращается в следующую:

. (6.2.4)

Очевидно, что матрица вероятностей перехода за 2 шага может быть получена умножением матрицы (6.2.2) на себя:

(6.2.5)

Обобщением формулы (6.2.5) является следующая формула для матрицы вероятностей перехода за m шагов:

(6.2.6)

Введем p_i(k) как вероятность того, что на k-м шаге система будет находиться в состоянии s_i,. Тогда матрица - строка p(k) = ( p₁(k); …; p_n(k) ) является матрицей состояния системы на k-м шаге. Для однородной цепи Маркова имеет место следующая формула:

^, (6.2.7)

где p(0) определяет начальное состояние системы.

В цепях Маркова с конечным числом состояний находят применение графы состояний, в которых показаны возможные состояния системы (изображаются кружками) и переходные вероятности (изображаются стрелками).

Задача.6.3.1 В моменты времени t₁, t₂, t₃ происходит осмотр ЭВМ, возможные состояния которой: s₁ – полностью исправная ЭВМ; s₂ – незначительные неисправности, которые позволяют эксплуатировать ЭВМ; s₃ – существенные неисправности, но дающие возможность решать ограниченное число задач; s₄ – ЭВМ вышла из строя. Граф состояний имеет следующий вид:

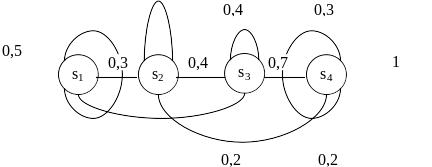
Найти: а) матрицу переходных вероятностей; б) вероятности состояний ЭВМ после 1,2 осмотров, если вначале (при t=0) ЭВМ была исправна.

Решение. а) по графу состояний построим матрицу переходных вероятностей

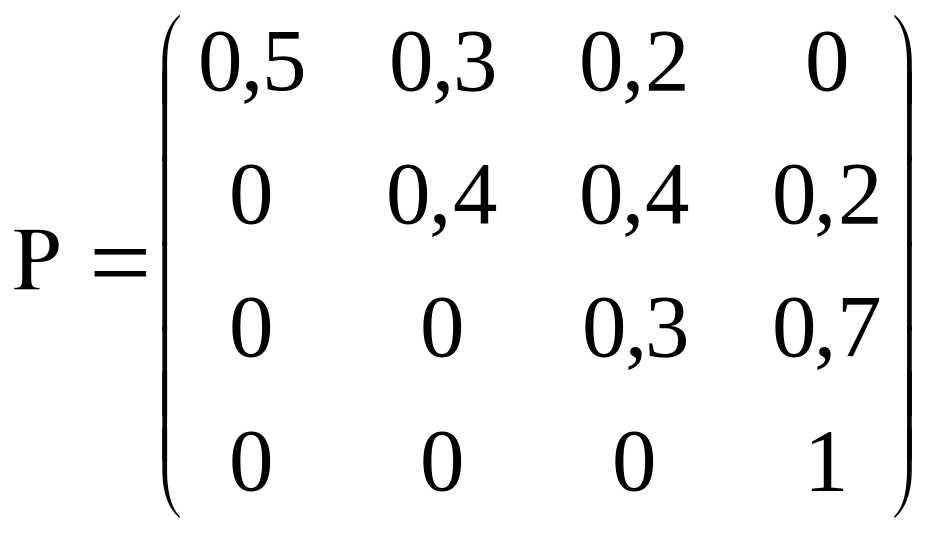
б) p(0) = (1;0;0;0); p(1) = p(0) ; p(1) =(0,5; 0,3; 0,2; 0);

p(2) = (0,25; 0,27; 0,28; 0,2).