6. Случайные процессы. Марковские случайные процессы. Системы массового обслуживания
6.1. Случайные процессы
Вначале введем понятие случайной функции.
Определение 6.1.1. Случайной функцией X(t) называют функцию неслучайного аргумента t, которая при каждом фиксированном значении аргумента является случайной величиной.
Иными словами, при t = t0 X(t0) представляет собой случайную величину, сечение случайной функции в момент времени t0.
С другой точки зрения, ввиду того, что случайная величина представляется в виде функции элементарного события ω, появляющегося в результате испытания, случайную функцию можно записать в виде функции двух переменных X(t, ω), где ω є Ω , t єT.
Определение 6.1.2. Реализацией случайной функции X(t, ω), называется неслучайная функция x(t), в которую обращается случайная функция в результате испытания при фиксированном ω.
Реализацию случайной функции называют также траекторией , выборочной случайной функцией. Таким образом, случайную функцию можно рассматривать как совокупность ее возможных реализаций (рис. 6.1.1).
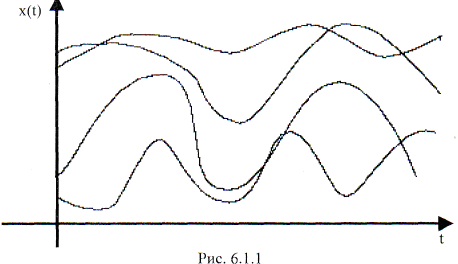
Определение 6.1.3. Случайным процессом называют случайную функцию аргумента t, который истолковывается как время.
В дальнейшем мы будем иметь дело со случайными процессами.
Пример 6.1.1. Самолет должен лететь на задаваемой автопилотом высоте. В действительности, вследствие воздействия случайных факторов (колебание температуры, изменение плотности, давления в атмосфере, изменение силы и направления ветра и др.), учесть влияние которых исчерпывающим образом невозможно, высота меняется во времени. Поэтому высота полета представляет собой случайный процесс.
При фиксированном t = t1 X(t1) является случайной величиной, которая имеет свой закон распределения – например, в случае случайной величины непрерывного типа, плотность вероятности f1(x1, t1) или, если t принимает все допустимые значения, - f1(x, t). Неслучайная функция f1(x, t) называется одномерной плотностью вероятности случайного процесса. Функция f1(x, t) полностью характеризует каждое отдельно взятое сечение, однако, нельзя сказать, что она полностью описывает случайный процесс X(t).
Если взять два сечения X1 = X(t1) и X2 = X(t2) в виде системы (X1,X2), рассматривают двумерную плотность вероятности f(x1,x2); в теории случайных процессов её обозначают f2(x1,x2;t1,t2). Двумерный закон распределения описывает случайный процесс более полно, чем одномерный; однако и он исчерпывающим образом не описывает случайный процесс X(t).
В результате для более полного описания случайных процессов переходят к многомерным (n-мерным) законам распределения в виде n-мерной плотности вероятности f2(x1,x2, ..., xn; t1,t2, ..., tn).
Однако в ряде случаев для описания случайного процесса достаточно ограничиться его числовыми характеристиками. В рамках ирреляционной теории случайных процессов ограничиваются изучением моментов первого и второго порядков.
Определение 6.1.4. Математическим ожиданием случайного процесса X(t) называется неслучайная функция mx(t), которая при любых значениях переменной t равна математическому ожиданию соответствующего сечения случайного процесса.
Определение 6.1.5. Дисперсией случайного процесса X(t) называется неслучайная функция Dx(t), которая при любом значении переменной t равна дисперсии соответствующего сечения случайного процесса.
Математическое ожидание и дисперсия случайного процесса обладают свойствами, аналогичными соответствующим свойствам случайных величин.
Определение 6.1.6. Корреляционной функцией случайного процесса X(t) называется неслучайная функция Kx(t1,t2) двух переменных t1 и t2, которая для любой пары переменных t1 и t2 равна корреляционному моменту (ковариации) соответствующих сечений случайного процесса.
Корреляционная функция Kx(t1,t2) характеризует не только степень связи между двумя любыми сечениями случайного процесса, но и степень рассеяния этих сечений относительно математического ожидания mx(t).