5.4. Центральная предельная теорема

Рассмотрим вопрос, связанный с предельным законом распределения суммы , когда число слагаемых неограниченно возрастает. Центральная предельная теорема устанавливает условия, при которых указанный предельный закон является нормальным.

Определение 5.4.1. Пусть последовательность случайных величин. Говорят, что последовательность сходится к случайной величине по распределению, если

(5.4.1)

в каждой точке x непрерывности ; здесь – функция распределения случайной величины Х; – функция распределения случайной величины X_n.

Центральная предельная теорема допускает несколько формулировок. Одна из наиболее простых форм ее имеет вид:

Теорема 5.4.1. ЦПТ-1. Пусть - последовательность независимых и одинаково распределенных случайных величин, для которых . Тогда последовательность ,

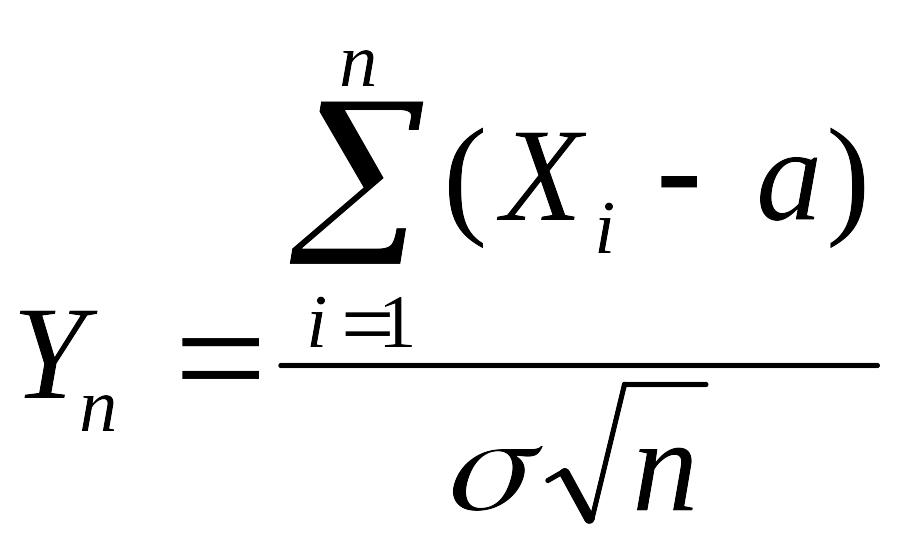(5.4.2)

сходится по распределению к нормальному распределению , т.е.

, (5.4.3)

где – функция распределения случайной величины .

Из ЦПТ-1 вытекает, как частный случай, интегральная теорема Муавра-Лапласа.

Интегральная теорема Муавра-Лапласа. Пусть – число успехов в серии из испытаний, – вероятность успеха при каждом испытании. Тогда при

. (5.4.4)

Доказательство. Действительно, m=X₁+ X₂+ _... +X_n, где X_i – число успехов в ‑м испытании; – независимы и одинаково распределены. Кроме того, , . Подставляя эти выражения в формулу (5.4.2), из (5.4.3) получим (5.4.4), что и требовалось доказать.

Теперь избавимся от нежелательного в ряде вопросов предположения об одинаковом распределении случайных величин и сформулируем центральную предельную теорему в форме Ляпунова.

Теорема 5.4.2. Пусть – последовательность независимых случайных величин с и . Тогда, если выполнено условие Ляпунова

при , (5.4.5)

где , то последовательность {Y_n}, где

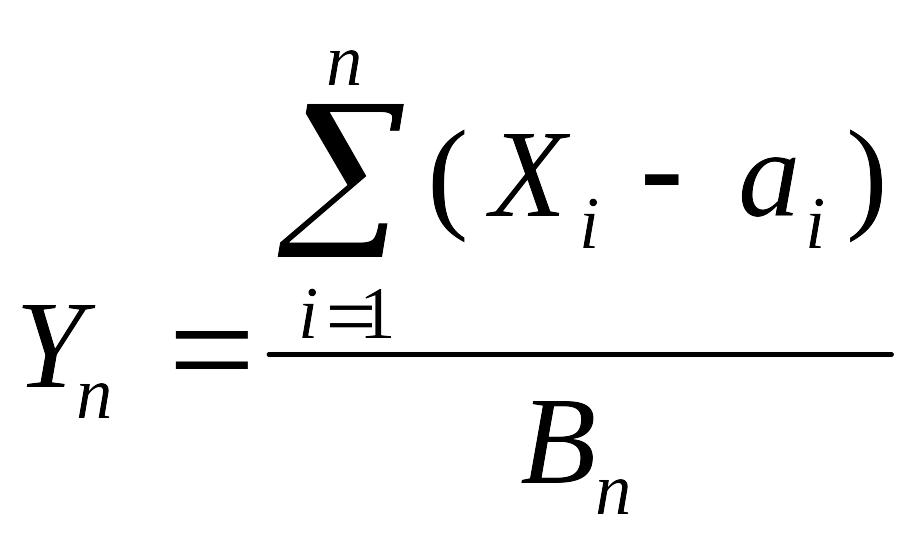, (5.4.6)

сходится по распределению к N(0, 1) равномерно на .

Покажем на примерах случаи применения центральной предельной теоремы.

Пример 1. Вероятность и частота.

Оценим с помощью центральной предельной теоремы 5.4.1 вероятность того, что частота отличается от вероятности успеха в испытаниях Бернулли по модулю меньше (или не меньше) чем на произвольное . Имеем

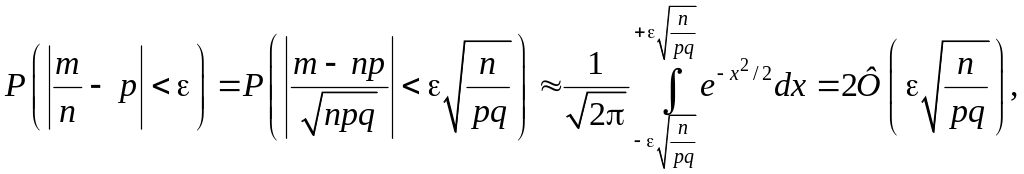
где 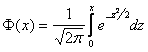– функция Лапласа.

Таким образом имеем

. (5.4.7)

С другой стороны,

.

Пример 2. Среднее арифметическое. Пусть X₁, X₂, ... попарно независимые случайные величины, . Закон больших чисел в форме теоремы Чебышева (5.2.4) имеет вид 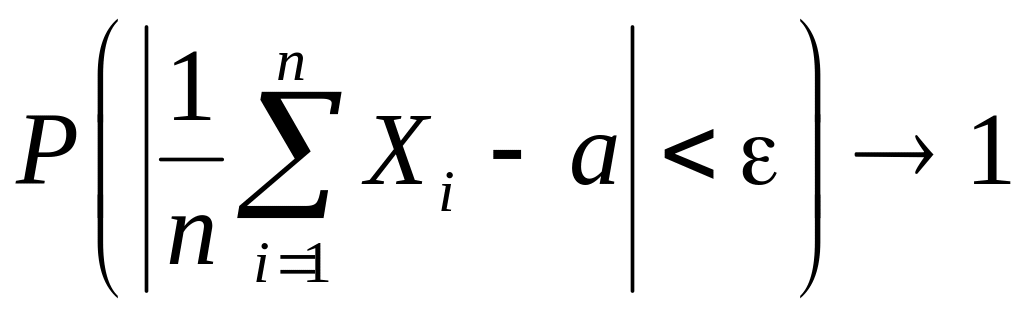, при .

Если , ... не только попарно независимы, но и независимы в совокупности, можно применить теорему 5.4.1. Это дает:

.

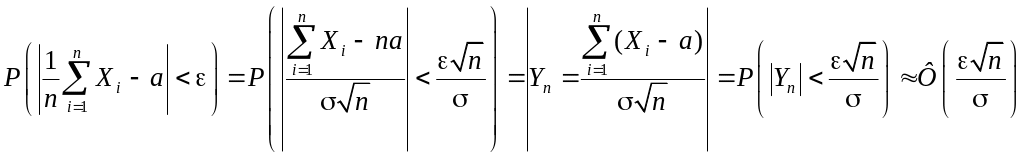^{Поэтому имеем}

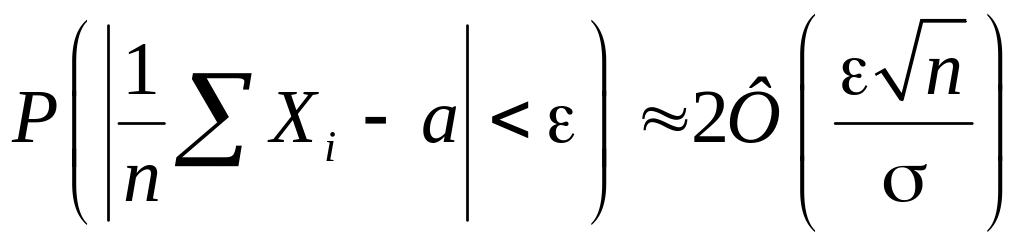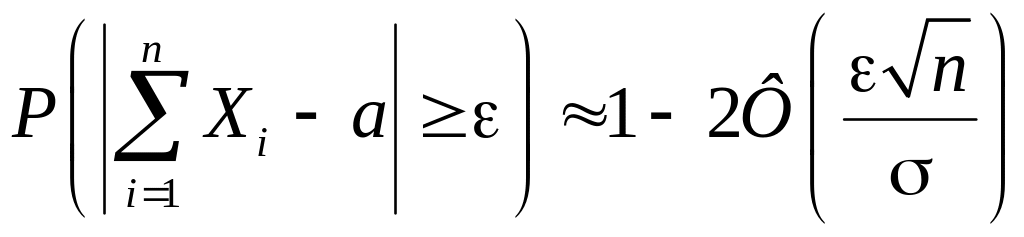, (5.4.8)

Из табл. 4 для функции Лапласа Ф(х) следует, что при =3, т.е. при вероятность

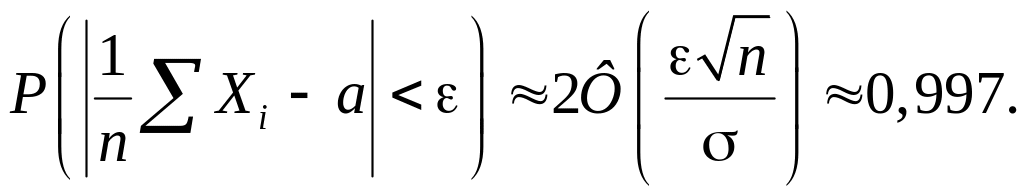
Это так называемое правило 3 (трех сигм).

Задача 5.4.1. Производится 500 испытаний, в каждом из которых вероятность наступления события А равна 0,3. Какова вероятность того, что частота наступления события А отклонится от его вероятности по модулю меньше, чем на 0,05?

Решение: Используя формулу (5.4.7.), имеем

, поэтому

.