5.2. Теорема Чебышева

Теорема Чебышева является одной из важнейших форм закона больших чисел.

Определение 5.2.1. Пусть имеем последовательность случайных величин:

(5.2.1)

Последовательность (5.2.1), т.е. , называется сходящейся по вероятности к случайной величине , если для любого при . Записывается:

при . (5.2.2)

Лемма Чебышева 2. Пусть имеем последовательность случайных величин, причем , при . Тогда при .

Доказательство. Применим 2-е неравенство Чебышева к случайной величине X_n:

, так как при _. В силу того, что МХ =0, из последнего неравенства имеем Р( при п , а это означает, что при .

Теорема Чебышева. Пусть – последовательность попарно независимых случайных величин, дисперсии которых ограничены в совокупности: . Тогда последовательность сходится по вероятности к нулю, т.е. для при , иначе

при . (5.2.3)

Доказательство: Рассмотрим случайную и найдем математическое ожидание и дисперсию . Имеем

;

, так как по условию . Но величина при , тогда при . Поэтому для последовательности выполняются условия леммы 2 , а значит, при , что и требовалось доказать.

Частный случай. Пусть при условиях теоремы Чебышева i = 1, 2, …, тогда из теоремы Чебышева следует, что для любого

при ; значит

при . (5.2.4)

Теорема Чебышева имеет большое практическое значение и устанавливает связь между средним арифметическим наблюдаемых в опыте значений случайной величины и ее математическим ожиданием; оказывается, эта случайная величина является устойчивой в том смысле, что при соблюдении некоторых условий сходится по вероятности к определенной неслучайной величине.

5.3. Теорема Бернулли

Теорема Я.Бернулли является исторически первой формой закона больших чисел. Она устанавливает связь между частотой некоторого события (успеха) в схеме независимых испытаний Бернулли и его вероятностью. Доказательство, данное Бернулли, было весьма сложным. Простое доказательство было дано П.Л.Чебышевым как прямое следствие его теоремы.

Теорема Бернулли. Пусть имеем схему независимых испытаний Бернулли и р-вероятность успеха в каждом испытании. Тогда частота успехов в испытаниях стремится по вероятности к р при , т.е.

при _. (5.3.1)

Доказательство. Для схемы независимых испытаний Бернулли относительная частота успехов является случайной величиной.

Пусть X₁ – число успехов в 1-м испытании, X₂ – число успехов во 2-м испытании и т.д., X_n – число успехов в -испытании. Тогда

X1	0	1
P	q	p

,

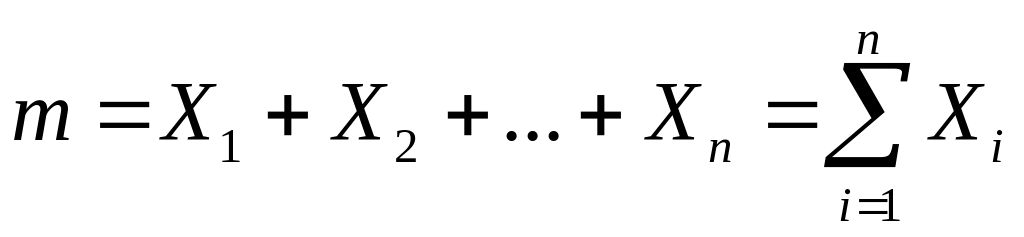. Аналогично, для любого i = 1, 2, …, n. Имеем

,

.

Используя частный случай теоремы Чебышева, имеем

при .

Теорема Бернулли является теоретическим обоснованием практического определения вероятностей с помощью относительной частоты (например, практическое определение вероятности выпадения герба при достаточно большом числе бросаний монеты). Закон больших чисел Бернулли утверждает, что для любого ε>0 и для фиксированного достаточно большого очень правдоподобно, что частота будет отклоняться от вероятности по модулю меньше, чем на . Отсюда, однако, не следует, что останется малой для всех достаточно больших п. Теорема Бернулли гарантирует лишь, что эти отклонения могут появляться весьма редко.