4. Функции случайных величин

4.1. Преобразование случайных величин (случай двух переменных)

Пусть имеем систему двух случайных величин непрерывного типа и – плотность распределения этой системы. Пусть имеем функциональное преобразование этой системы в , осуществляемое с помощью уравнений:

_. (4.1.1)

Ставится задача: найти плотность распределения системы .

Пусть преобразование (4.1.1) осуществляет взаимно однозначное отображение плоскости в плоскость . Это означает, что существует обратное преобразование или в координатной форме

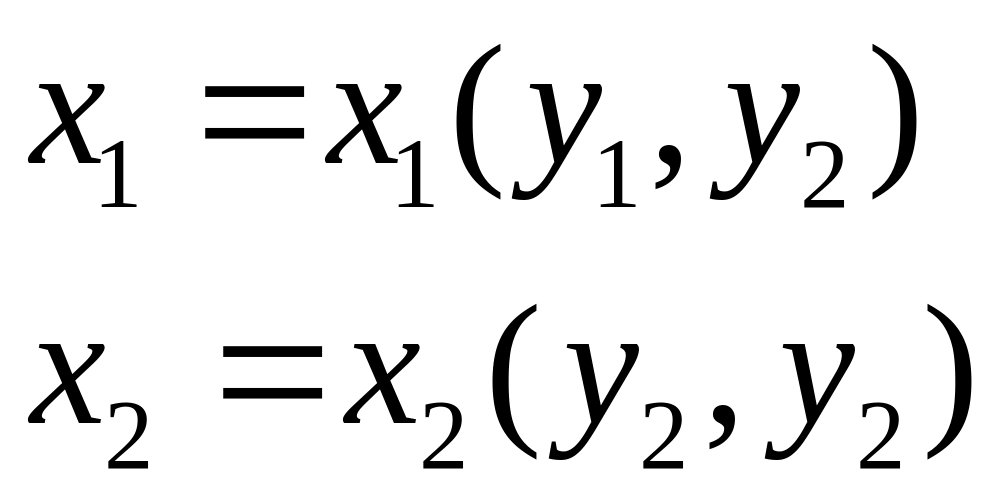_. (4.1.2)

Это возможно, если якобиан отображения (4.1.2) отличен от нуля в рассматриваемой области плоскости : J= .

Обозначая через Ф(y₁,y₂) функцию распределения системы , имеем

,

где .

С другой стороны, .

Здесь .

Переходя к новым переменным , с помощью преобразования (4.1.2) в последнем двойном интеграле имеем:

.

Сравнивая два последних двойных интеграла по области G, имеем

. (4.1.3)

4.2. Распределение суммы, разности, произведения и частного двух случайных величин

1. Пусть имеем две случайные величины X и Y; известна совместная плотность распределения их . Требуется найти плотность распределения суммы .

Рассмотрим преобразование , откуда , .

Тогда по формуле (4.1.3) совместная плотность вероятности имеет вид

.

Найдем теперь одномерную (маргинальную) плотность случайной величины :

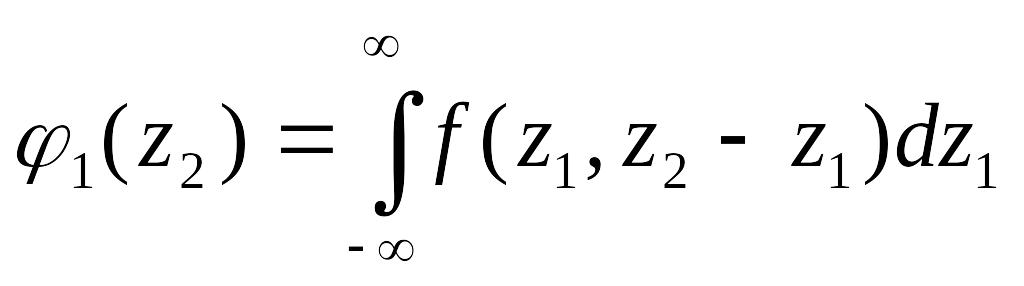
или

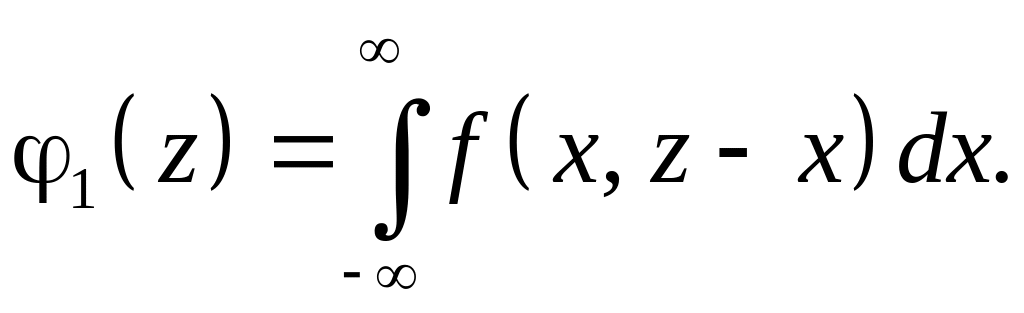(4.2.1)

Если X и Y – независимые случайные величины, то формулу (4.2.1) можно переписать в следующем виде:

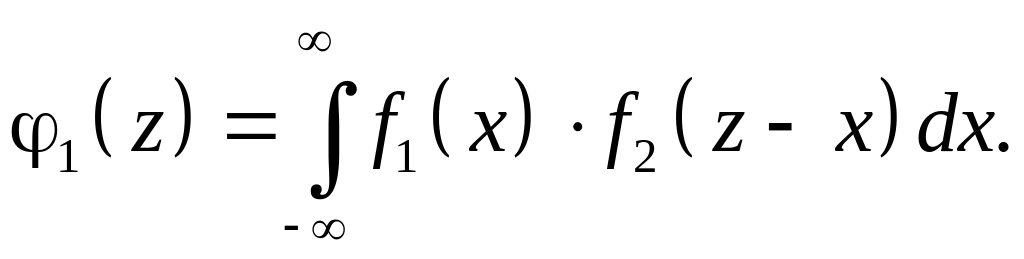(4.2.2)

Распределение суммы независимых величин X и Y называют композицией распределений этих величин.

2. Пусть Z = X - Y, требуется найти . Рассмотрим преобразование

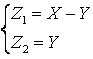, откуда ,

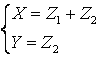Тогда _; , или, обозначая , имеем

. (4.2.3)

Для независимых X и Y получаем

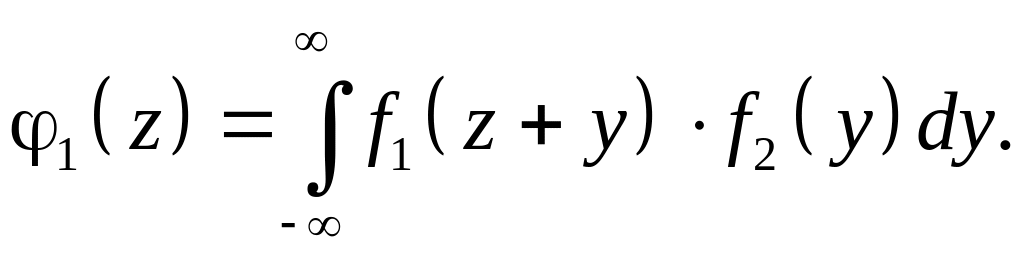(4.2.4)

3. Пусть , найдем .

Рассмотрим преобразование: 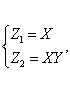откуда

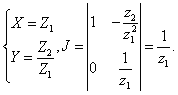
Тогда . Имеем далее .

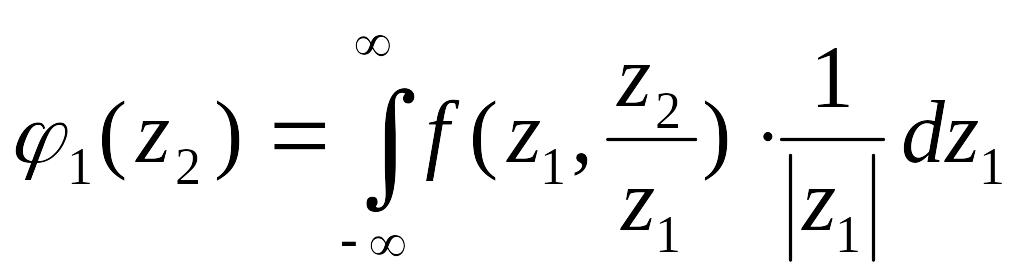Обозначая , получим 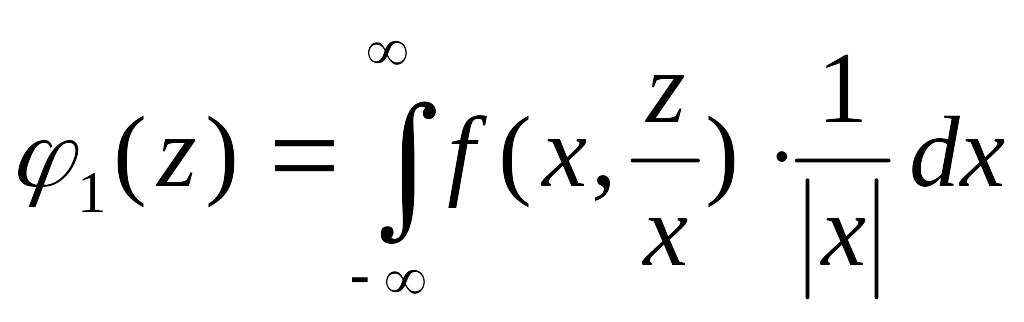. (4.2.5)

Для независимых случайных величин X и Y последняя формула переписывается в виде

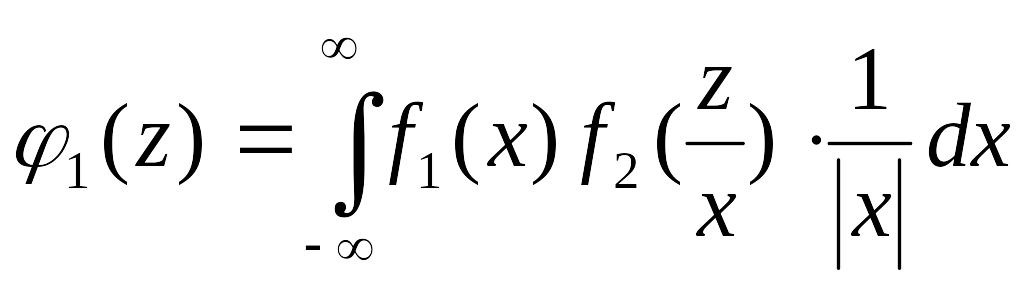. (4.2.6)

4. Наконец, пусть . Найдем .

Рассмотрим преобразование: 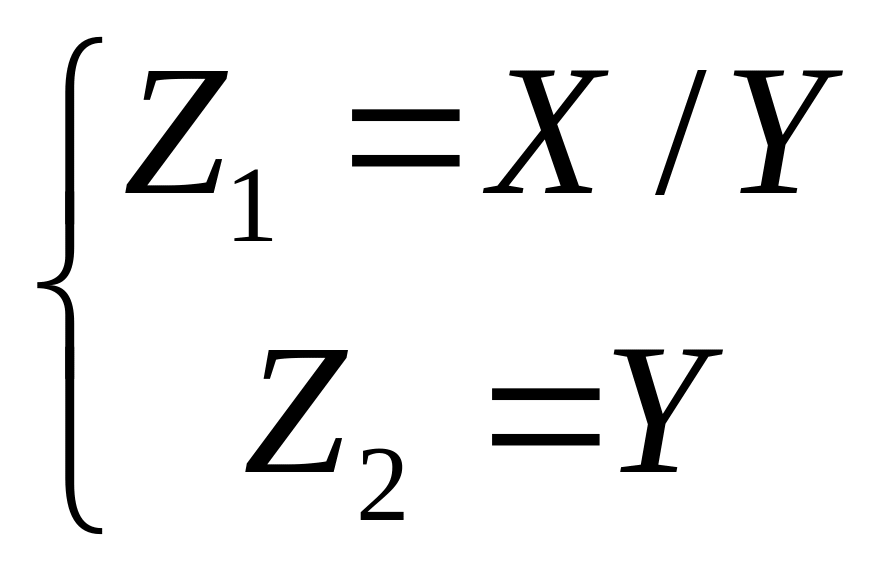, откуда , .

Тогда . Имеем далее .

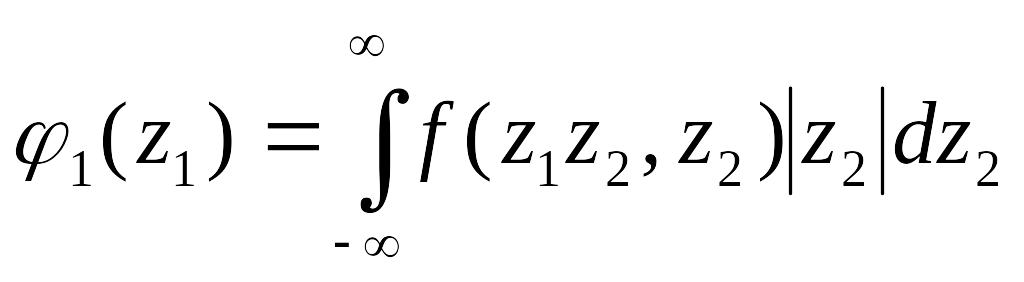Обозначая , имеем

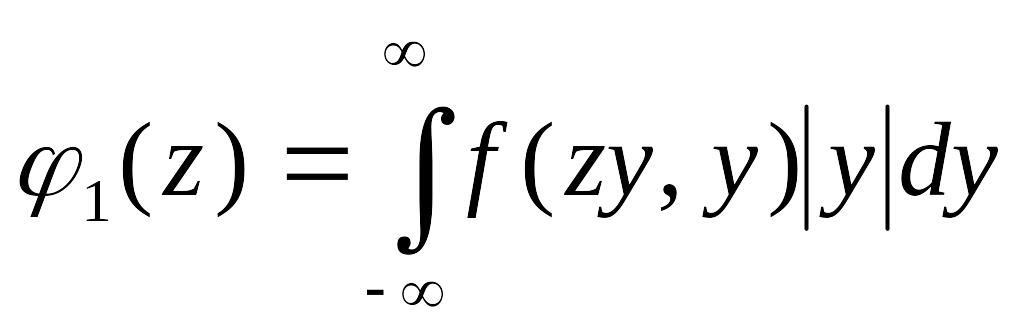. (4.2.7)

В случае независимых случайных величин X и Y, формулу (4.2.7) можно переписать в виде

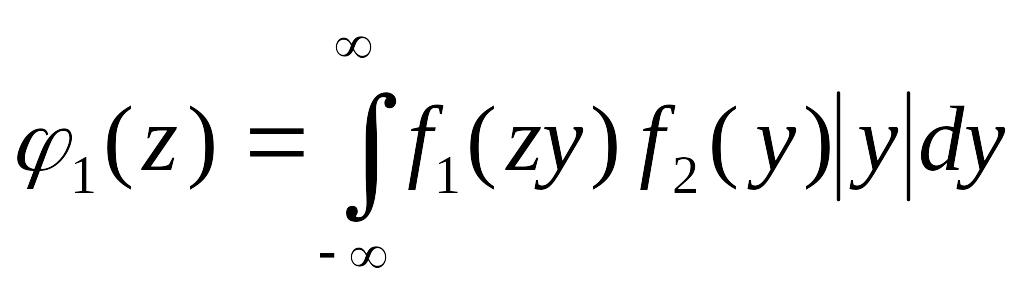. (4.2.8)

Задача 4.2.1. Найти закон распределения суммы независимых нормально распределенных случайных величин X и Y с параметрами .

Решение. Плотности вероятностей случайных величин X и Y имеют вид

, .

Используя формулу (4.2.2) для композиции этих случайных величин, имеем

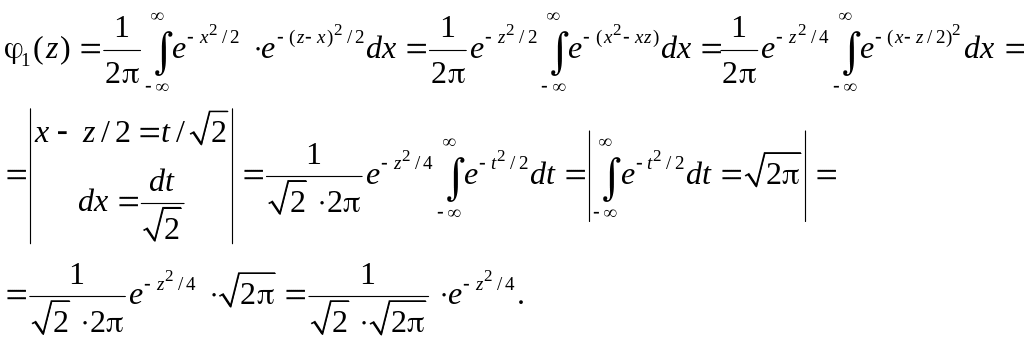
Последняя функция является плотностью нормального распределения с параметрами .

Можно показать, что имеет место более общий результат относительно суммы (композиции) любого конечного числа независимых случайных величин с нормальным распределением.

Теорема 4.2.1. Пусть - независимые случайные величины, каждая из которых имеет нормальное распределение с параметрами соответственно. Тогда композиция этих случайных величин является также нормальным распределением с параметрами:

; ^(4.2.9)

Приведем также без доказательства обратную теорему.

Теорема 4.2.2 (Крамер). Если сумма n независимых случайных величин имеет нормальное распределение, то каждая из величин распределена по нормальному закону.

Таким образом, верно не только то, что нормальное распределение воспроизводит само себя, но, кроме того, то, что нормальное распределение не может быть представлено как композиция не нормально распределенных компонент.

Кроме того, так как случайная величина X, являющаяся линейной комбинацией независимых нормально распределенных случайных величин , является нормально распределенной с параметрами , , то отсюда вытекает важная для дальнейшего теорема.

Теорема 4.2.3. Если случайные величины независимы и имеют нормальное распределение , то среднее арифметическое имеет нормальное распределение с параметрами .