3.3. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции

Законы распределения системы случайных величин являются ее исчерпывающими вероятностными характеристиками. Однако в случае, если закон распределения системы неизвестен (или не может быть построен), используют числовые характеристики системы.

Определение 3.3.1. Начальным моментом порядка k+s системы (X,Y) называется математическое ожидание произведения k-й степени X на s-ю степень Y:

. (3.3.1)

Формулы для начальных моментов имеют следующий вид:

- для системы (X,Y) дискретного типа

; (3.3.2)

- для системы (X,Y) непрерывного типа:

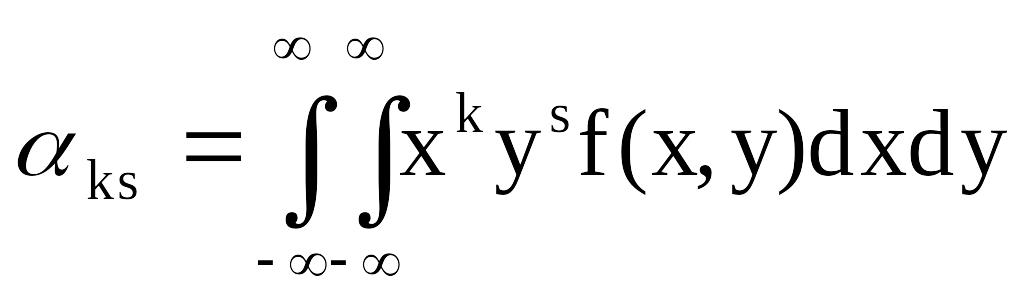. (3.3.3)

На практике наиболее употребительными являются начальные моменты первого порядка: , , которые являются математическими ожиданиями компонент системы (X,Y).

Точку называют центром рассеивания системы на плоскости.

Определение 3.3.2. Центральным моментом порядка k+s системы (X,Y) называется математическое ожидание произведения k-й и s-й степеней соответствующих центрированных величин:

. (3.3.4)

Формулы для вычисления моментов имеют следующий вид:

- для системы (X,Y) дискретного типа

; (3.3.5)

- для системы (X,Y) непрерывного типа

. (3.3.6)

Наибольшее применение имеют центральные моменты второго порядка. Два из них представляют собой известные ранее дисперсии величин X и Y:

,

.

Особую роль играет второй смешанный центральный момент , который называется корреляционным моментом. Он обозначается:

. (3.3.7)

Формулы для вычисления корреляционного момента имеют вид:

- для системы (X,Y) дискретного типа

; (3.3.8)

- для системы (X,Y) непрерывного типа

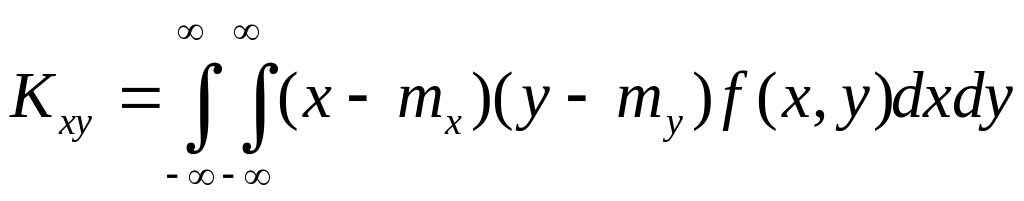. (3.3.9)

Корреляционный момент характеризует, помимо рассеяния системы (X,Y) относительно точки рассеивания, степень связи между компонентами X и Y.

Определение 3.3.3. Случайные величины X и Y называются некоррелированными, если = 0.

Связь между некоррелированностью и независимостью выражается следующей теоремой.

Теорема 3.3.1. Если случайные величины X и Y независимы, то они некоррелированны.

Доказательство. Пусть X, Y - независимые случайные величины. Тогда, используя теорему о математическом ожидании произведения независимых случайных величин, имеем . Но, очевидно, (и аналогично . Тогда .

Обратная теорема не имеет места, т. е. из некоррелированности случайных величин X и Y, вообще говоря, не вытекает их независимость.

Пример 3.3.1. Пусть система (X, Y) имеет равномерное распределение внутри круга , причем . Тогда

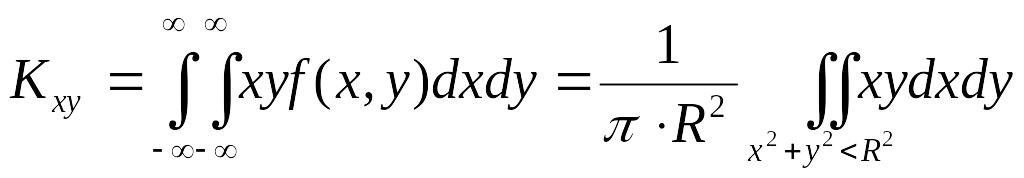= 0.

Следовательно, случайные величины X и Y некоррелированны. Но, с другой стороны, эти случайные величины являются зависимыми (см. задачу 3.2.2).

Пример 3.3.2. Показать, что в случае нормального распределения системы (X,Y) из некоррелированности вытекает их независимость.

Действительно, в случае нормального распределения плотность распределения системы имеет вид

.

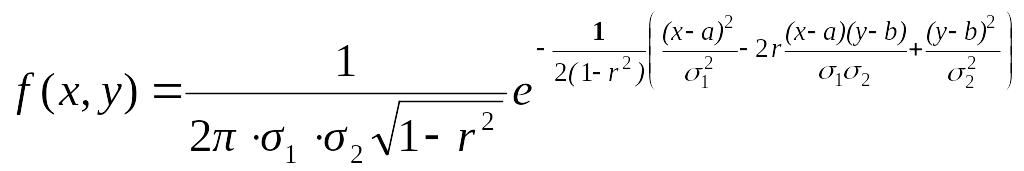Если компоненты X и Y некоррелированные, то r = 0 и имеет место равенство

,

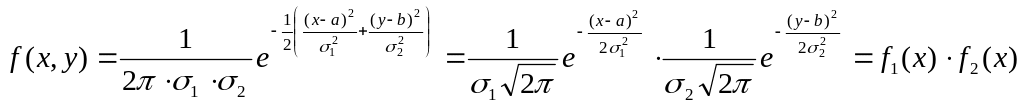что и означает независимость случайных величин X и Y.

Для оценки степени связи обычно используют безразмерное отношение

, (3.3.10)

которое называется коэффициентом корреляции случайных величин X и Y.

Можно показать, что , поэтому . Если , то говорят, что между X и Y существует положительная корреляция; это означает, что с увеличением значений одной случайной величины, другая имеет тенденцию к возрастанию. Если , то говорят, что между X и Y существует отрицательная корреляция; это означает, что с увеличением значений одной случайной величины другая имеет тенденцию к убыванию. Если , это означает, что случайные величины X и Y некоррелированны.

Если между случайными величинами X и Y существует линейная зависимость, то . Действительно, пусть . В этом случае

;

.

Тогда

.

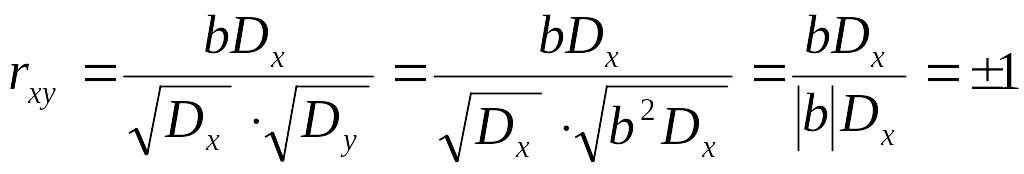Информацию о связи между компонентами X и Y системы (X,Y) несет корреляционная матрица , которая имеет вид

.

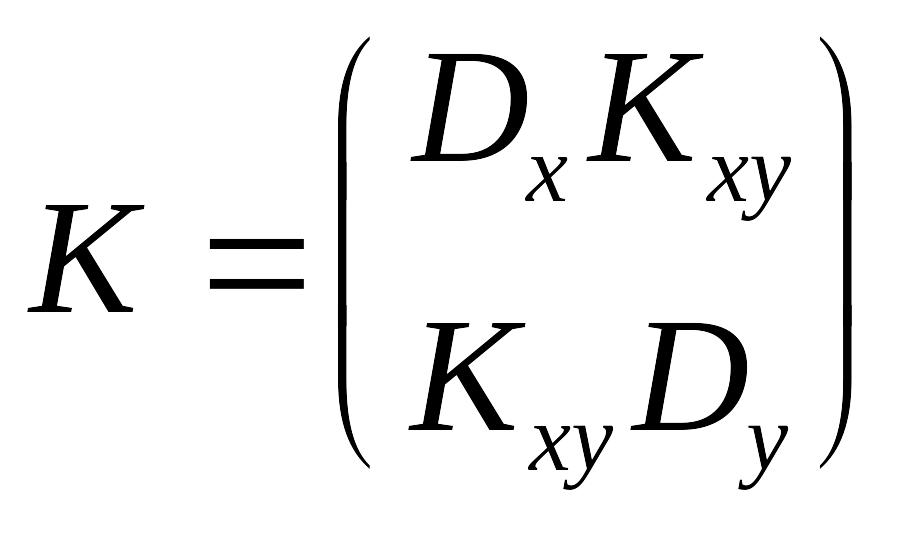Матрица К является симметричной вследствие равенства .

Кроме корреляционного момента и коэффициента корреляции , взаимная связь двух случайных величин может быть описана с помощью линий регрессии.

Действительно, при каждом значении Х = х величина Y остается случайной величиной, допускающей рассеяние своих значений, однако зависимость Y от Х сказывается также в изменении средних значений Y при переходе от одного значения X к другому. Эту зависимость и описывает кривая регрессии

. (3.3.11)

Аналогично, зависимость X от Y, которая сказывается в изменении средних значений X при переходе от одного значения Y = y к другому, описывается кривой регрессии

. (3.3.12)

Наиболее простым случаем будет тот, когда обе функции (3.3.11) и (3.3.12) линейны, так что обе линии регрессии будут прямыми линиями; они называются прямыми регрессии. В этом случае будем говорить о линейной корреляции между случайными величинами X и Y.

Выведем уравнения прямых регрессии. Пусть MX = m_x, MY = m_y, D_x = , D_y =  , K_xy – корреляционный момент случайных величин X и Y. Будем искать уравнение прямой регрессии Y на X в виде , где параметры A и B подлежат определению.

Взяв математическое ожидание от обеих частей последнего равенства и учитывая, что , имеем, что . Далее

, откуда .

Таким образом, в случае линейной корреляции уравнение прямой регрессии Y на X имеет вид

.

Аналогично уравнение прямой регрессии X на Y имеет вид

.

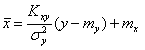Если учесть, что , то уравнения прямых регрессии могут быть переписаны в симметричной форме:

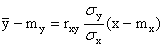; (3.3.13)

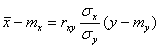. (3.3.14)

Из уравнений прямых регрессии (3.3.13) и (3.3.14) видно, что обе прямые проходят через точку (m_x,m_y). Угловые коэффициенты прямых регрессии равны соответственно:

, .

Так как , прямая регрессии Y на X имеет меньший угол наклона к оси Ох, чем прямая регрессии X на Y. Чем ближе к 1, тем меньше угол между этими прямыми; при = 1 прямые регрессии сливаются. При прямые регрессии имеют уравнения и , так что обе они параллельны соответствующим осям координат. В этом случае величины X и Y являются некоррелируемыми; для них , , т. е. условные математические ожидания совпадают с безусловными.