3.2. Условные законы распределения. Зависимые и независимые случайные величины

Если известно распределение системы двух случайных величин (например, совместная плотность X и Y – f(x,y)), легко получить распределение каждой из величин, входящей в систему (например, с помощью формулы (3.1.6)). Если теперь перейти к обратной задаче: по известным законам распределения отдельных компонент системы X и Y, найти закон распределения системы - эта задача в общем случае неразрешима. Дело в том, что законы распределения каждой из случайных величин, входящих в систему, характеризуют каждую из случайных величин в отдельности, но ничего не говорят о том, как они связаны между собой; совместный закон распределения X и Y (закон распределения системы (X, Y)) должен содержать все сведения о компонентах системы, в том числе и о характере связей между ними. Это приводит к необходимости введения условных законов распределения.

Определение 3.2.1. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения этой случайной величины.

Пусть (X, Y) является системой дискретного типа и закон распределения ее представлен табл. 3.1.1.

Пусть в результате испытания случайная величина Y приняла значение ; при этом X примет одно из своих возможных значений с вероятностями соответственно. Обозначим условную вероятность того, что X примет, например, значение x_i при условии, что , через P(x_i/y_j); она, вообще говоря, не будет равна безусловной вероятности P(x_i).

Условным распределением компоненты X системы при называется совокупность условных вероятностей:

. (3.2.1)

Аналогично определяется условное распределение компоненты Y системы (X,Y).

Используя теорему умножения двух случайных событий, соответствующих данной ситуации, условный закон распределения X при условии, что может быть найден по формулам:

.

Вероятность (безусловная) вычисляется по формуле .

Аналогично находят условные законы распределения компоненты Y системы (X,Y) двух случайных величин непрерывного типа. Тогда условной плотностью компоненты X при данном значении Y = y называют отношение плотности совместного распределения системы (X,Y) к плотности компоненты Y:

. (3.2.2)

Различие между условной плотностью и безусловной плотностью состоит в том, что функция определяет распределение X при условии, что Y принимает значения Y = y, а функция определяет распределения X независимо от того, какие значения принимает Y.

Аналогично определяется условная плотность компоненты Y при данном значении X = x:

. (3.2.3)

Формулы (3.2.2) и (3.2.3) можно записать в виде

. (3.2.4)

Как и любая плотность распределения, условные плотности обладают следующими свойствами:

^{; .}

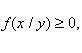
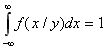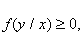
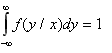Задача 3.2.1. Система двух случайных величин (X,Y) определена следующей таблицей распределения:

Таблица 3.2.1

X\Y
	0,15	0,30
	0,06	0,10
	0,25	0,03
	0,04	0,07

Найти условный закон распределения компоненты Х при условии, что компонента Y приняла значение y₂=6.

Решение. Условный закон распределения компоненты X при условии, что , определяется совокупностью вероятностей: . Принимая во внимание, что , имеем:

Задача 3.2.2. Система (X,Y) имеет равномерное распределение внутри круга . Найти условные законы распределения компонент X и Y.

Решение. Совместная плотность равномерного распределения внутри круга имеет вид 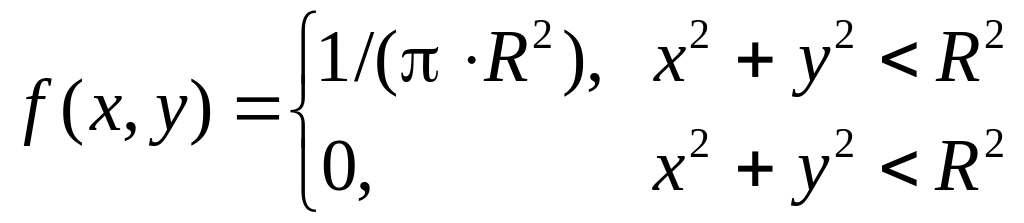. Найдем сначала условную плотность составляющей X при , при Y = y, |y|<R; имеем

.

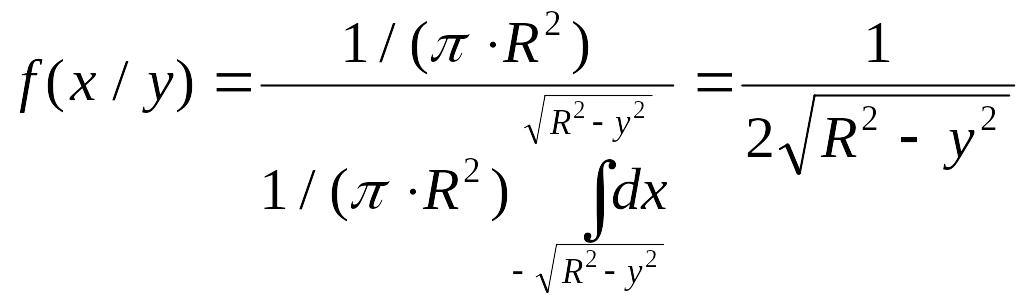Так как f(x,y)=0 при , то при . Окончательно

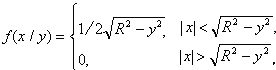(3.2.5)

Аналогично, условная плотность компоненты Y имеет вид

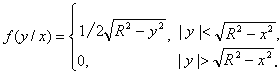. (3.2.6)

Ранее мы считали две случайные величины независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая случайная величина. Отсюда следует, что условные законы распределения независимых случайных величин равны их безусловным законам. Например, в случае когда система (X,Y) является системой непрерывного типа, это приводит к равенствам , , и, следовательно, в силу формул (3.2.2) и (3.2.3), имеем

. (3.2.7)

Условие (3.2.7) (и это можно строго доказать) является необходимым и достаточным условием того, чтобы случайные величины X и Y были независимыми.