3. Системы случайных величин

3.1. Закон распределения системы двух случайных величин. Функция распределения, плотность распределения системы двух случайных величин

При изучении случайных явлений в зависимости от их сложности приходится рассматривать две, три и большее число случайных величин. Например, точка попадания снаряда определяется не одной, а двумя случайными величинами: абсциссой и ординатой. Совместное рассмотрение двух или нескольких случайных величин приводит к системе случайных величин. Условимся обозначать систему нескольких случайных величин (X, Y, Z, ..., W). При изучении системы случайных величин недостаточно изучить отдельные составляющие системы случайных величин; необходимо учитывать еще и связи, зависимость между ними.

В дальнейшем мы будем рассматривать систему двух случайных величин (X, Y). При этом удобно пользоваться геометрической интерпретацией системы, а именно, систему двух случайных величин (X, Y) можно рассматривать как случайную точку на плоскости xOy с координатами X и Y или как случайный вектор на плоскости со случайными составляющими X и Y.

Пусть X и Y – случайные величины дискретного типа. Тогда закон распределения системы (X, Y) может быть представлен в виде таблицы распределения системы дискретных случайных величин.

Таблица 3.1.1

X\Y			· · ·
			· · ·
			· · ·
·	·	·	· · ·	·
			· · ·

Здесь .

Все возможные события , i = 1, ..., m; j = 1, ..., n образуют полную группу попарно несовместных событий, поэтому .

Определение 3.1.1. Функцией распределения системы двух случайных величин называется функция двух аргументов , равная вероятности совместного выполнения двух неравенств , т. е.

(3.1.1)

Геометрически функция распределения системы двух случайных величин (X, Y) представляет собой вероятность попадания случайной точки (X, Y) в левый нижний бесконечный квадрант плоскости с вершиной в точке (x, y) (рис. 3.1.1).

Д

Рис. 3.1.1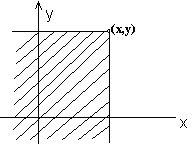

анная геометрическая интерпретация позволяет наглядно проиллюстрировать следующие свойства функции распределения системы двух случайных величин.

Свойство 1. Если один из аргументов стремится к , то функция распределения системы стремится к функции распределения одной случайной величины, соответствующей другому аргументу, т. е.

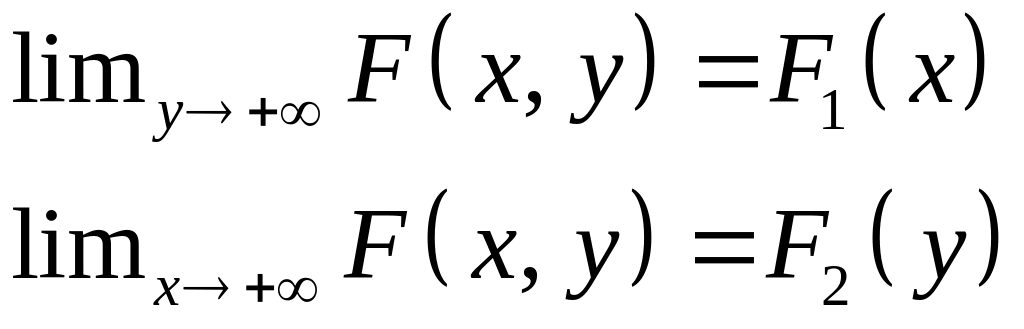или

Доказательство легко провести, отодвигая одну из границ квадранта на рис. 3.1.1 в ; при этом в пределе квадрант превращается в полуплоскость (рис. 3.1.2, 3.1.3).

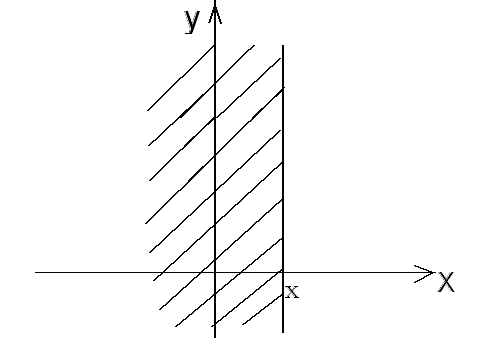
Рис. 3.1.2 Рис. 3.1.3

Вероятность же попадания случайной точки в такую полуплоскость есть функция распределения одной из величин, входящих в систему.

Свойство 2. Если оба аргумента стремятся к , то функция распределения системы стремится к единице, т. е. или .

Доказательство. Действительно, при квадрант на рис. 3.1.1 с вершиной (x, y) обращается во всю координатную плоскость xOy; попадание же случайной точки в нее является достоверным событием.

Свойство 3. При стремлении одного или обоих аргументов к функция распределения стремится к нулю, т.е. или .

Доказательство. Действительно, отодвигая ту или иную границу квадранта (или обе границы) в минус бесконечность, убеждаемся, что происходит вырождение квадрата, и поэтому вероятность попадания случайной точки в квадрат в пределе равна нулю.

Свойство 4. Функция распределения F(x, y) является неубывающей функцией по каждому аргументу, т.е. для : ; для : .

Доказывается аналогично на основе геометрической интерпретации функции распределения системы двух случайных величин.

Функция распределения системы двух случайных величин является универсальной характеристикой (законом) системы двух случайных величин, так как применяется для описания систем как дискретных, так и непрерывных случайных величин. Система двух случайных величин непрерывного типа характеризуется плотностью вероятности распределения системы двух случайных величин.

Определение 3.1.2. Система двух случайных величин (X, Y) называется непрерывной, если существует кусочно-непрерывная неотрицательная функция и такая, что для любых x, yR имеет место равенство

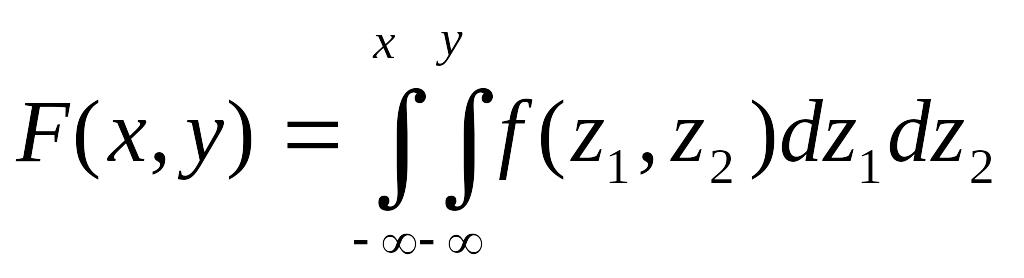. (3.1.2)

Функция f(x,y) называется плотностью вероятности системы двух случайных величин или, иначе, совместной плотностью случайных величин X и Y.

Плотность вероятности обладает следующими свойствами

Свойство 1. В точках непрерывности f(x,y) справедливо равенство

. (3.1.3)

Свойство 2. Для любой области имеем

. (3.1.4)

Свойство 3 (условие нормировки).

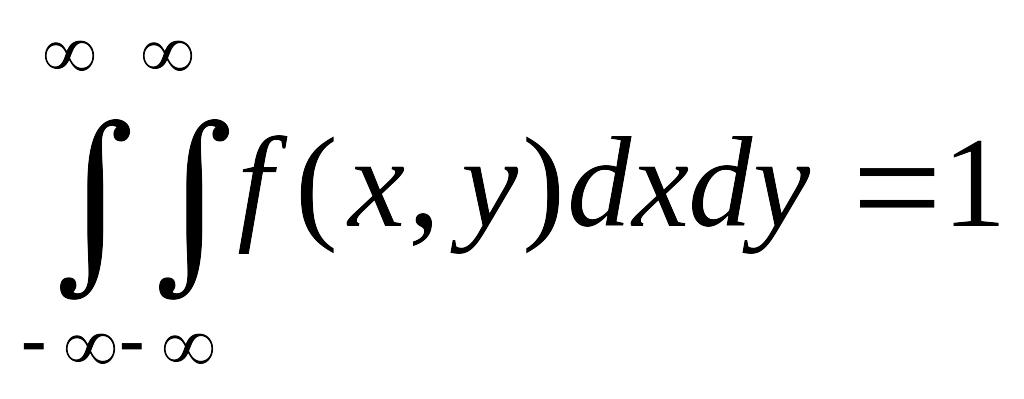. (3.1.5)

Свойство 4. Каждая компонента непрерывной системы двух случайных величин имеет плотность вероятности, которая вычисляется по одной из формул:

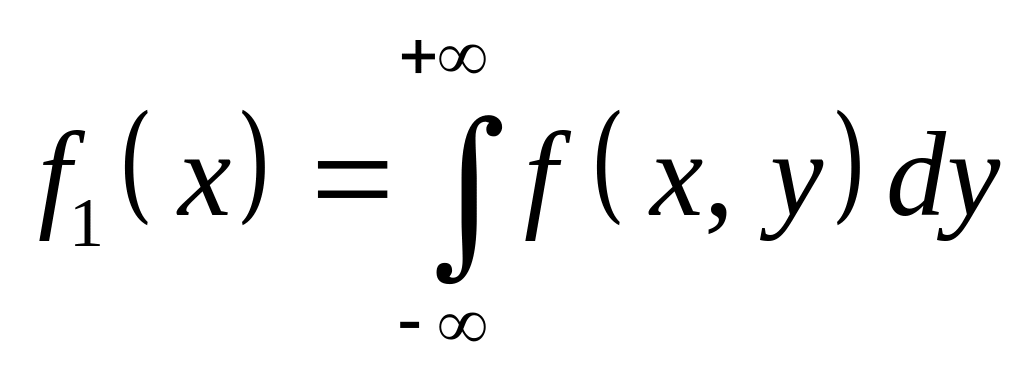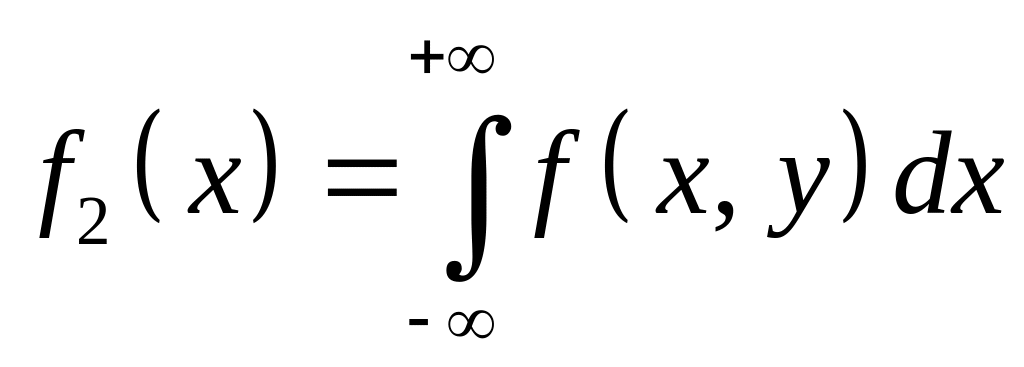, . (3.1.6)

Доказательство свойства 3. На основании формул (3.1.2) и свойства 2 для F(x,y) имеем

.

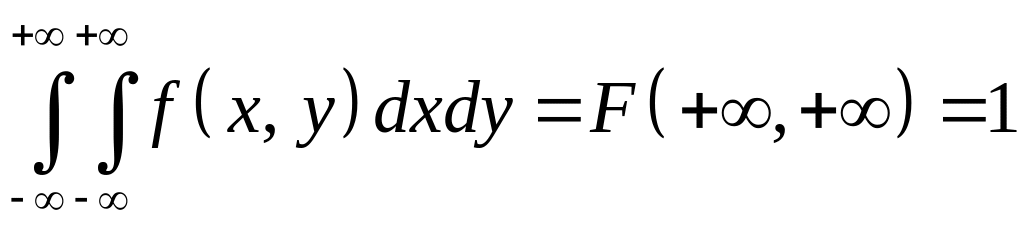Доказательство свойства 4. С одной стороны, . С другой стороны, .

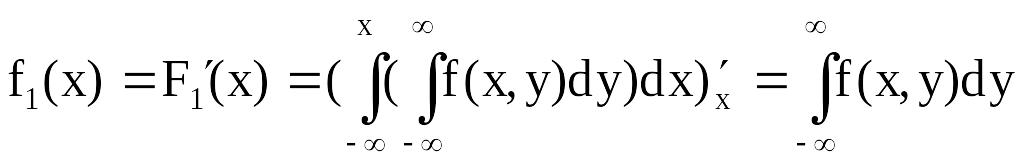Примеры наиболее важных систем двух случайных величин

1. Равномерное распределение в области D системы двух случайных величин (X, Y)

Система двух случайных величин (X, Y) называется равномерно распределенной в области D, если совместная плотность f(x,y) случайных величин X и Y имеет вид

_.

Постоянная С может быть определена из условия нормировки (3.1.5): , откуда . Здесь S(D) – площадь области D. Поэтому

. (3.1.7)

2. Нормальное распределение вектора (X, Y.)

Случайный вектор (X, Y) называется распределенным по нормальному закону (закону Гаусса), если

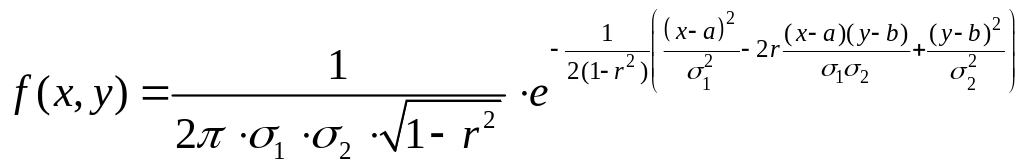_. (3.1.8)

Это распределение имеет пять параметров: . Можно показать, что , , r – коэффициент корреляции, выражающий связь между компонентами X и Y случайного вектора (X, Y).