2.4. Пуассоновский поток событий

Пусть некоторое случайное событие А (называемое в дальнейшем “успехом”) может происходить случайным образом в течение времени t. Свяжем с этим потоком событий случайную величину X(t), являющуюся числом наступления “успехов” в течение времени t. Пусть этот поток событий обладает следующими свойствами.

1. Отсутствие последействия. Для любых непересекающихся интервалов времени длиной t₁, t₂, …, t_k случайные величины X(t₁), X(t₂), …,X(t_k) являются независимыми.

2. Стационарность. Случайная величина X(t) зависит лишь от величины t интервала и не зависит от его начала, поэтому интервал может быть взят с началом в точке t = 0.

3. Ординарность. Для любых малых промежутков времени Δt имеет место равенство

P(X(Δt) = 1) = λΔt + o(Δt), λ>0,

где λ – интенсивность потока случайных событий.

Свойство ординарности означает, что для малых промежутков времени Δt “успех” может наступить лишь один раз (или не наступить вообще), а вероятность наступления “успеха” большее число раз является бесконечно малой величиной большего порядка чем Δt.

Поток случайных событий, обладающий свойствами отсутствия последействия, стационарности и ординарности, называется пуассоновским (простейшим) потоком случайных событий.

Найдем (при этих условиях) вероятность того, что в течение времени t “успех” наступит k раз, т.е. величину P(X(t) = k).

Разделим интервал (0,t) на n частей с длиной Δt = t/n. На каждом таком частичном интервале длиной Δt введем величины p₁ = P(X(Δt) = 1) = λΔt + o(Δt),

p₀ = P(X(Δt) = 0) = 1-λΔt + o(Δt).

Тогда искомая вероятность может быть вычислена по формуле Бернулли. Имеем .

Последняя формула может быть преобразована в следующую:

.

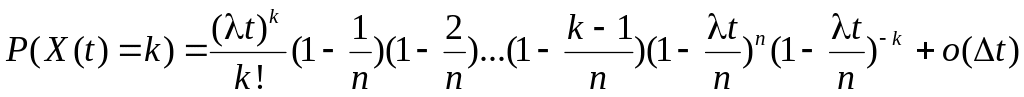Переходя к пределу при , получим

. (2.4.1)

Формулу (2.4.1) также называют формулой Пуассона.

Страхование. Договоры страхования заключаются для того, чтобы избавиться от финансовых потерь, связанных со случайным характером тех или иных событий, т.е. с риском. После заключения договора, заплатив некоторую неслучайную сумму S₀, клиент избавляется от этого риска; его принимает на себя страховая компания. Но страховые договоры порождают иски: один в случае страхования жизни или несколько, например, в случае автострахования. Если X(t) – число исков, поступивших за время t, в динамической модели исков считают процесс поступления их пуассоновским. Во-первых, процессы поступления исков за непересекающиеся промежутки времени являются независимыми. Во-вторых, процесс является стационарным, т.е. распределение числа исков, поступивших за любой интервал (t₀, t₀+t) зависит только от его длины t. В-третьих, процесс является ординарным в том смысле, что поступление 2-х или более исков за малый промежуток времени практически не возможен.

Таким образом, вероятность любого числа исков, поступивших за время t, определяется формулой Пуассона (2.4.1); она же является основной при расчете величины страхового взноса.

Вопросы для самопроверки

1. Какая величина называется случайной величиной?

2. Дайте определение случайной величины дискретного и непрерывного типа. Привести примеры.

3. Что называется рядом распределения дискретной случайной величины?

4. Дайте определение функции распределения случайной величины. Перечислите ее свойства.

5. Дайте определение плотности вероятности случайной величины. Перечислите ее свойства.

6. Как, зная плотность вероятности случайной величины, найти вероятность попадания случайной величины в заданный интервал?

7. Дайте определение начального момента k-го порядка для случайной величины дискретного и непрерывного типа.

8. Что называется математическим ожиданием случайной величины дискретного типа?

9. Что называется математическим ожиданием случайной величины непрерывного типа?

10. Приведите свойства математического ожидания.

11. Дайте определение центрального момента k-го порядка случайной величины.

12. Что называется дисперсией случайной величины? Приведите формулы для дисперсии случайной величины дискретного и непрерывного типа.

13. Перечислите свойства дисперсии.

14. Какое распределение случайной величины называется биномиальным? Построить ряд распределения. Чему равны математическое ожидание и дисперсия этой случайной величины?

15. Какая случайная величина называется распределенной по закону Пуассона? Привести ее ряд распределения. Чему равны ее математическое ожидание и дисперсия?

16. Какое распределение случайной величины называется нормальным? Чему равны ее математическое ожидание и дисперсия?

17. Какое распределение случайной величины называется равномерным? Чему равно ее математическое ожидание?

18. Как найти вероятность попадания случайной величины с нормальным законом распределения в заданный интервал?

19. Какой поток случайных событий называется простейшим?

Задачи

1. Построить ряд распределения и функцию распределения числа попаданий мячом в корзину при двух бросках, если вероятность попадания равна 0,4.

Ответ:	X	0	1	2
	P	0,36	0,48	0,16

.

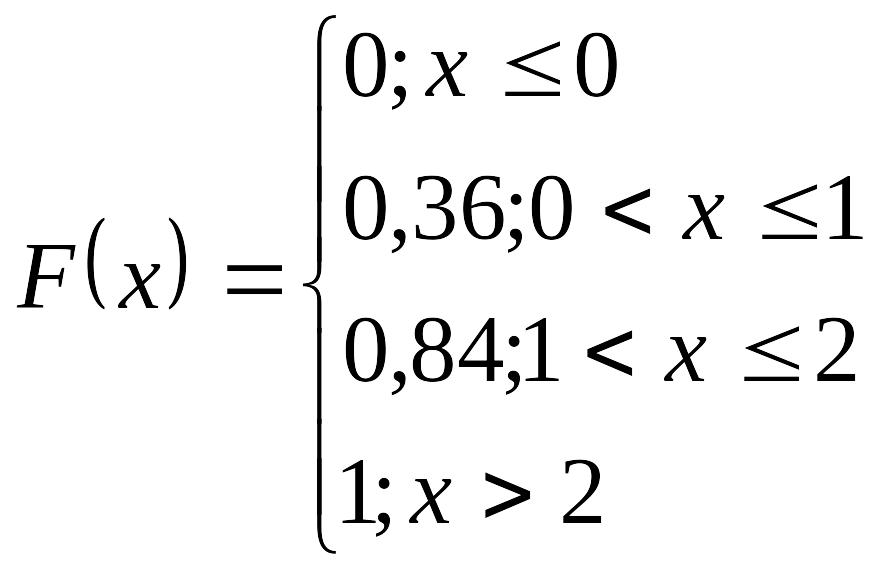
2. Из партии в 25 изделий, среди которых имеются 6 бракованных, выбраны случайным образом 3 изделия для проверки их качества. Построить ряд распределения числа бракованных изделий, содержащихся в выборке .

Ответ:	Х	0	1	2	3
	Р	0,42	0,45	0,12	0,01

3. Производится 5 бросаний ''правильной'' монеты. Построить ряд распределения числа ''гербов''. Найти математическое ожидание и дисперсию этой случайной величины.

Ответ:	X	0	1	2	3	4	5
	Р

MX = 5/2, DX = 5/4.

4. Случайная величина Х задана функцией распределения

. Найти коэффициент а. Написать выражение для плотности распределения. Определить математическое ожидание и дисперсию случайной величины.

Ответ: а = 1/2; ;

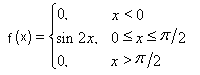MX = , DX = .

5. Функция распределения случайной величины Х задана формулой

F(x) = A + Barctgx, - < x < .

Найти: а) постоянные А и В; б) плотность вероятности f(x); в) вероятность того, что случайная величина Х попадет на отрезок [-1, 1].

Ответ: а) А = 1/2; В = 1/π ; б) f(x) = ; в) 1/2.

6. Случайная величина Х подчинена равномерному закону распределения на отрезке [1, 3]. Написать выражение для плотности распределения случайной величины Х. Найти математическое ожидание и дисперсию этой случайной величины.

Ответ: ; MX = 2; DX = 1/3.

7. Производится стрельба по цели независимыми выстрелами до первого попадания. Вероятность попадания в цель при одном выстреле равна р. Построить ряд распределения числа произведенных выстрелов. Найти математическое ожидание и среднее квадратическое отклонение числа произведенных выстрелов.

Ответ:	Х	1	2	3	...	n	...
	Р	р	Pq	pq2	...	pqn-1	...

MX = 1/p; .

8. Аппаратура содержит 1000 элементов, вероятность отказа для каждого из которых в течение некоторого времени Т равна 0,001 и не зависит от состояния других элементов. Какова вероятность отказа аппаратуры, если он наступает при отказе хотя бы одного из элементов.

Ответ: р = 1 – е^-1 0,63.

9. Телефонная станция обслуживает 500 абонентов. Вероятность позвонить на коммутатор любому абоненту в течение часа равна 0,01. Какова вероятность того, что в течение часа позвонят 3 абонента?

Ответ: р 0,14.

10. Ошибка измерения подчинена нормальному закону. Математическое ожидание этой ошибки равно 5м, а среднее квадратическое отклонение  10м. Найти вероятность того, что измеренное значение дальности будет отклоняться от истинного по модулю не больше, чем на 15м.

Ответ: р = 0,8187.