2.3. Числовые характеристики случайной величины. Математическое ожидание и дисперсия, их свойства

Довольно часто закон распределения, который полностью характеризует случайную величину, неизвестен. В этом случае используются ее числовые характеристики. К числу таких характеристик относятся начальные и центральные моменты различных порядков и, в частности, математическое ожидание и дисперсия случайной величины.

Определение 2.3.1. Начальным моментом k-го порядка называется:

1) для случайной величины дискретного типа:

; _; (2.3.1)

2) для случайной величины непрерывного типа:

. (2.3.2)

Определение 2.3.2. Если k = 1, начальный момент первого порядка ₁ называется математическим ожиданием случайной величины.

В этом случае из формул (2.3.1) и (2.3.2) получаем формулы для математического ожидания.

Для случайной величины дискретного типа:

MX = . (2.3.3)

Для случайной величины непрерывного типа:

MX = . (2.3.4)

Математическое ожидание выражает ''среднее'' значение случайной величины с учетом вероятностей ее значений.

Приведем в качестве примеров вычисление математических ожиданий для известных случайных величин.

Задача 2.3.1. Найти математическое ожидание случайной величины Х, которая принимает значения x₁, x₂, …,x_n, причем эти значения равновероятны.

Решение. Ряд распределения этой случайной величины имеет вид

X	x1	x2	...	xn
P	1/n	1/n	...	1/n

С помощью формулы (2.3.3) имеем

MX = .

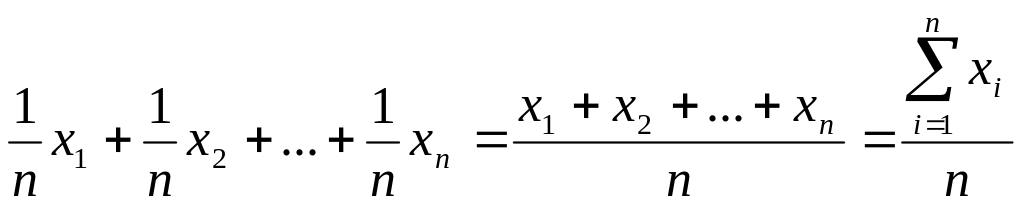Таким образом, математическим ожиданием этой случайной величины является среднее арифметическое ее значений.

Задача 2.3.2. Найти математическим ожиданием случайной величины с биномиальным законом распределения.

Решение. Ряд распределения случайной величины с биномиальным законом распределения имеет вид

X	0	1	2	...	n
P	Pn(0)	Pn(1)	Pn(2)	...	Pn(n)

где вероятности P_n(m) вычисляются по формуле Бернулли.

Имеем MX = 0∙P_n(0) + 1∙P_n(1) + 2∙P_n(2) + ... + n∙P_n(n) =

= npq^n-1 + 2 p²q^n-2 + ... + npⁿ = np (q^n-1 + (n-1)pq^n-2 + ... + p^n-1) = np(q+p)^n-1 = np.

Выше была использована формула для бинома Ньютона.

Задача 2.3.3. Найти математическое ожидание случайной величины, распределенной по закону Пуассона.

Решение. Ряд распределения случайной величины, распределенной по закону Пуассона, имеет вид

X	0	1	2	...	m	...
P				...		...

Здесь для вероятностей была использована формула Пуассона

Р(Х = m) = .

Имеем MX = 0e + 1 e + 2 e + ... = =

= e = e = e = e e = _.

Здесь было использовано разложение в ряд Маклорена e^x = ^.

Таким образом, МХ = .

Задача 2.3.4. Найти математическое ожидание случайной величины, имеющей равномерное распределение на отрезке [a, b].

Решение. Используя формулу (2.3.4), имеем (см. пример 1 п. 2.2):

MX = = = = .

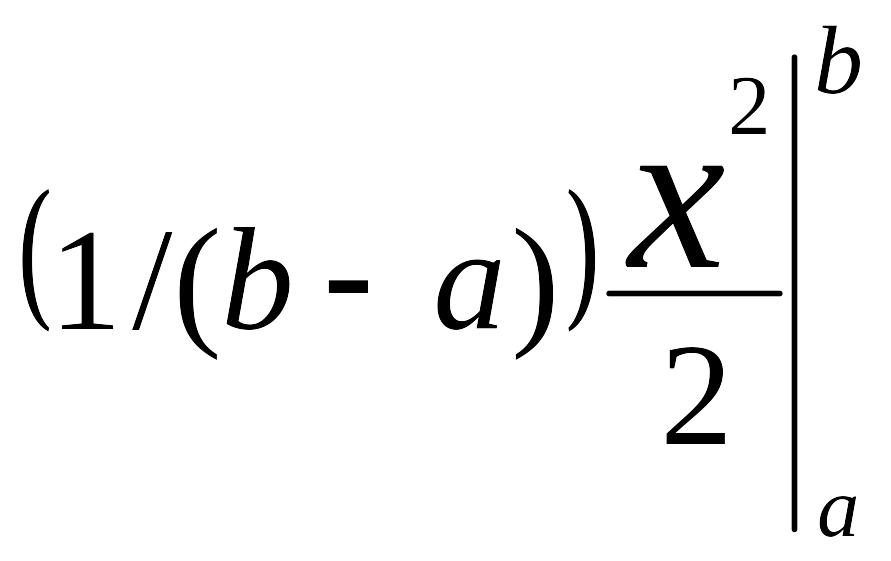Задача 2.3.5. Найти математическое ожидание случайной величины с нормальным законом распределения.

Решение. Используя формулу (2.3.4) и пример 2 п. 2.2, имеем:

MX = = = = =

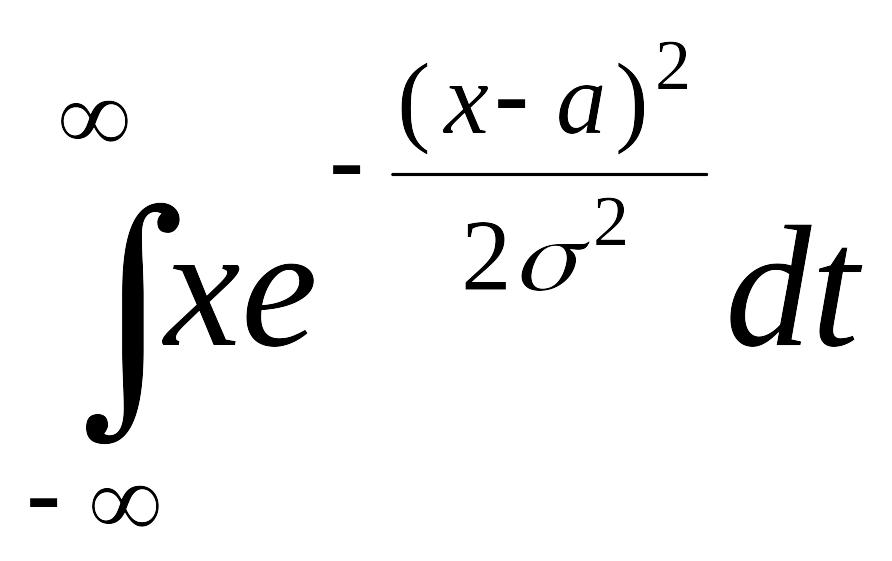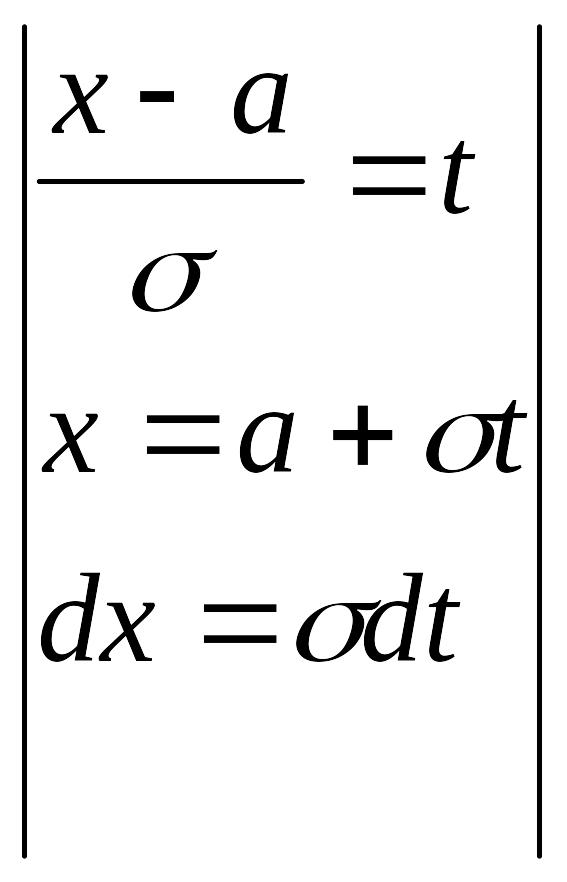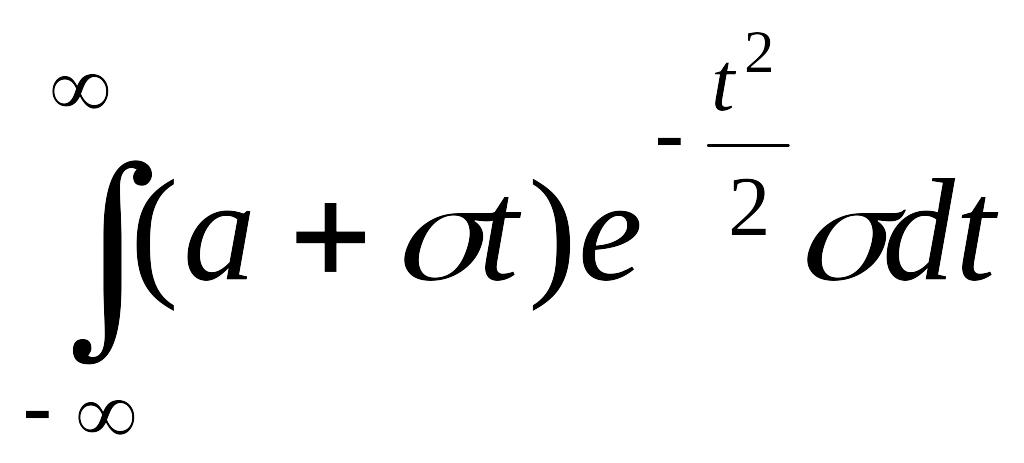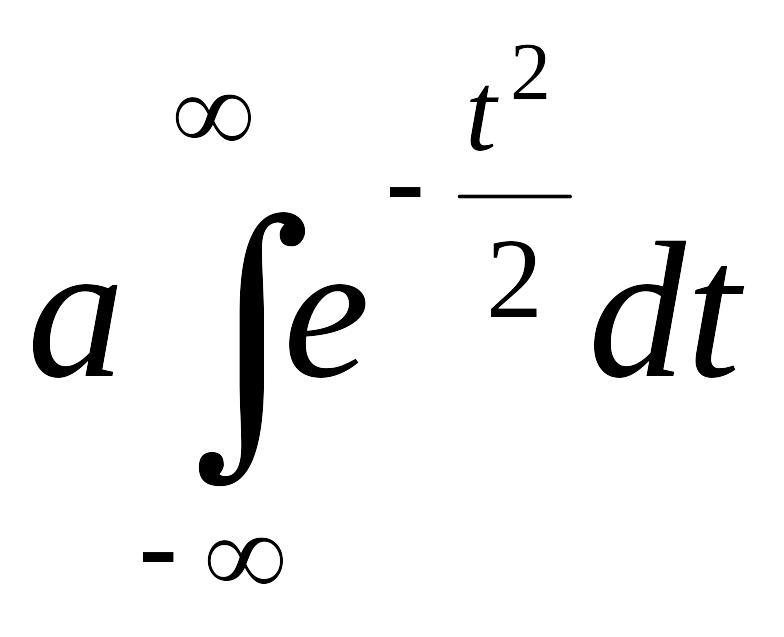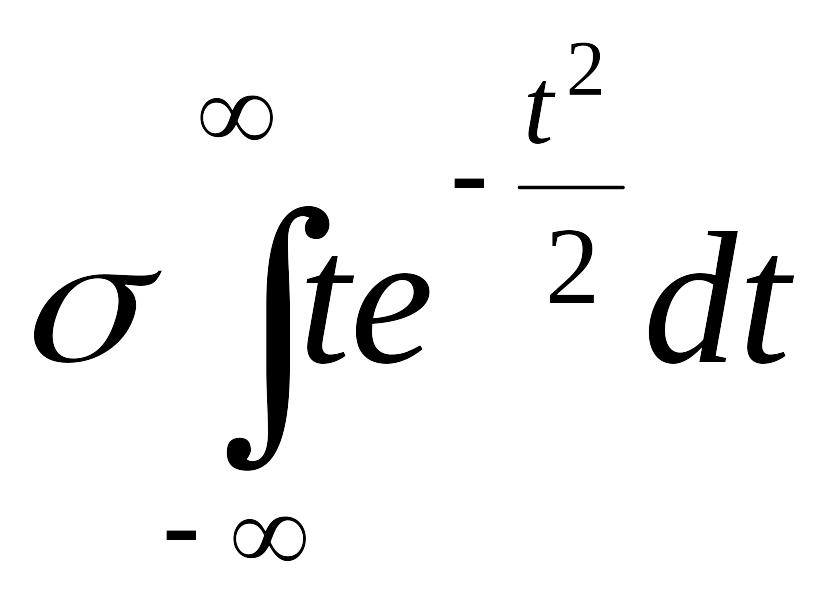= + = a,

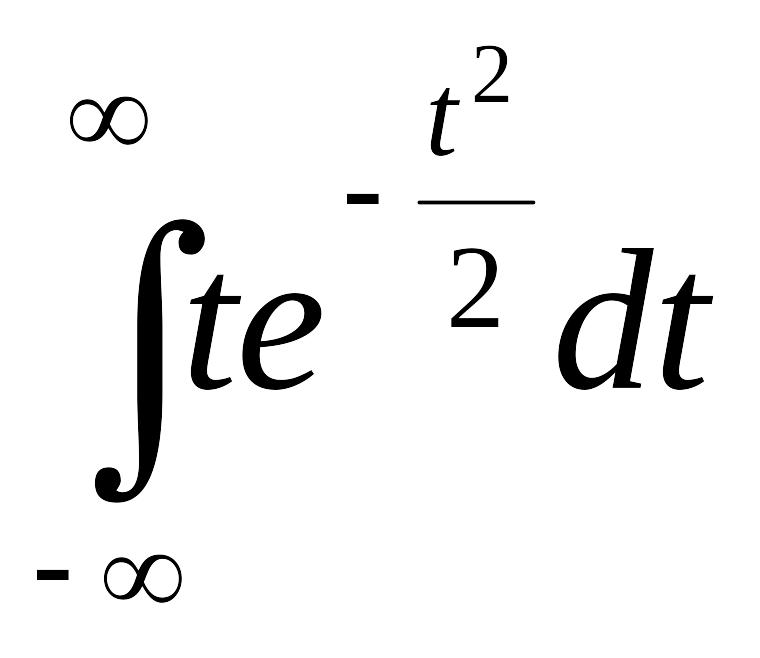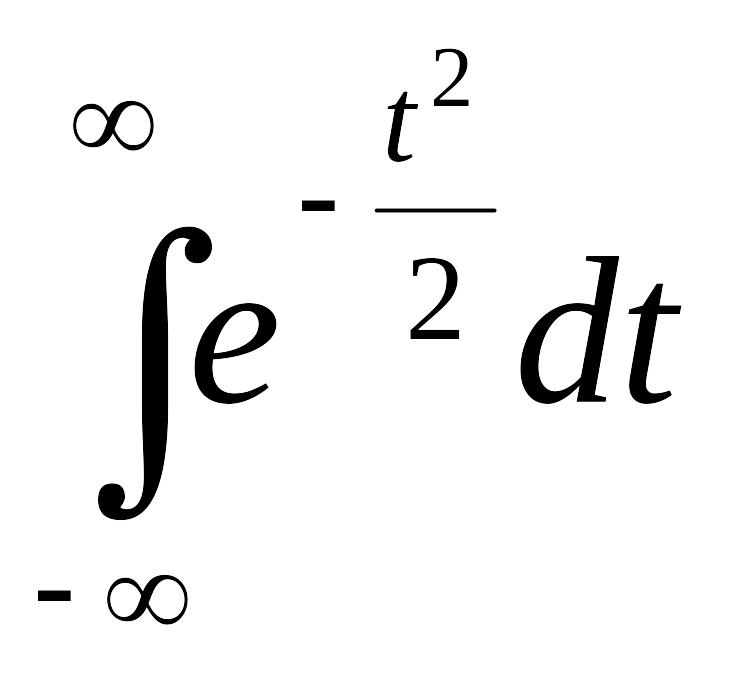так как = 0 и = , то MX = a.

Задача 2.3.6. Найти математическое ожидание случайной величины с показательным законом распределения.

Решение. Имеем:

MX = = 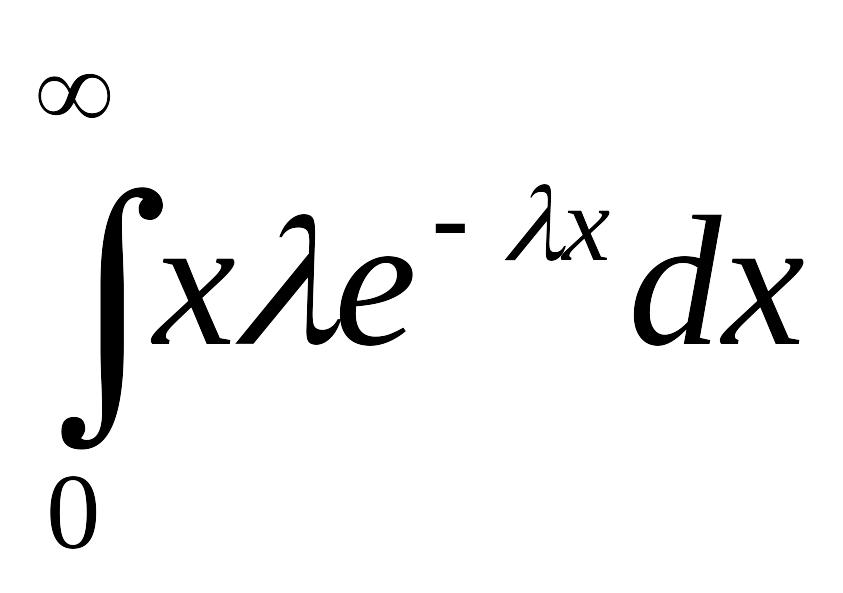= = 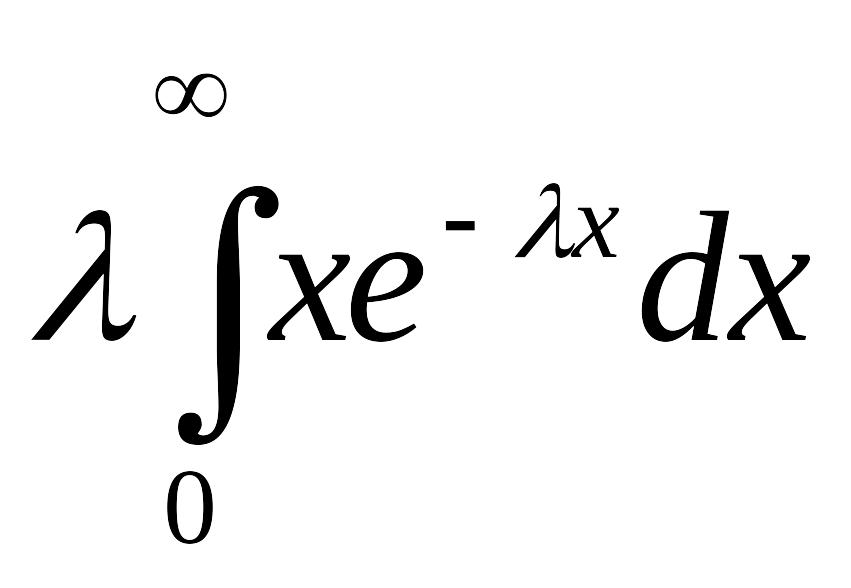1/λ .

Свойства математического ожидания.

Свойство 1. Математическое ожидание константы равно этой константе, т.е. М(С)=С.

Доказательство очевидно.

Свойство 2. М(СХ) = СМХ, иначе постоянный множитель можно выносить за знак математического ожидания.

Доказательство проведем для случая случайных величин дискретного типа. Имеем ряды распределения для случайных величин Х и СХ соответственно.

X	x1	x2	...	xn		CX	Cx1	Cx2	…	Cxn
P	p1	p2	…	pn		P	p1	p2	…	pn

Имеем М(СX) = = CMX .

Свойство 3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий, т.е.

M(X + Y) = MX + MY.

Доказательство аналогично доказательству свойства 2.

Определение 2.3.3. Две случайные величины X и Y называются независимыми, если закон распределения одной случайной величины не изменяется в зависимости от того, какие значения принимает другая случайная величина.

Приведем без доказательств 4 свойство случайной величины.

Свойство 4. Если две случайные величины X и Y независимы, то математическое ожидание их произведения равно произведению их математических ожиданий, т.е.

М(XY) = МХМY.

Определение 2.3.4. Центральным моментом k-го порядка случайной величины Х называется число µ_k = M (X - MX)^k, (2.3.5)

Поэтому для случайной величины дискретного типа имеем

µ_k = (x_i - MX)^k, (2.3.6)

а для случайной величины непрерывного типа –

µ_k = (x-MX)^kf(x)dx. (2.3.7)

Определение 2.3.4. При k = 2 центральный момент второго порядка µ₂ называется дисперсией случайной величины, т.е.

DX = M(X – MX)². (2.3.8)

Для случайной величины дискретного и непрерывного типов имеем соответственно формулы:

DX = (x_i - MX)² p_i , (2.3.9)

DX = (x -MX)²f(x)dx. (2.3.10)

Часто вместо формулы (2.3.8) для дисперсии используют другую формулу:

DX = MX² - (MX)². (2.3.11)

Действительно, DX = M(X - MX)² = M(X² - 2X MX + (MX)²) =

= MX² - 2MX MX + (MX)² = MX² - (MX)².

Величина =  называется средним квадратическим отклонением случайной величины Х. Дисперсия (как и среднее квадратическое отклонение) выражает меру рассеяния случайной величины Х относительно своего математического ожидания.

Свойства дисперсии

Свойство 1. Дисперсия константы равна нулю, т.е. DC = 0.

Доказательство. Имеем DC = M(C - MC)² = M(C - C)² = 0.

Свойство 2. D(CX) = C²DX, иначе постоянный множитель выносится с квадратом из-под знака дисперсии.

Доказательство. D(CX) = M(CX-M(CX))² = MC²(X-MX)² = C²M(X - MX)² = C²DX.

Свойство 3. Если Х и Y — независимые случайные величины, то дисперсия суммы случайных величин равна сумме их дисперсий, т.е.

D(X + Y) = DX + DY.

Доказательство. Имеем D(X+Y) = M((X+Y) - M(X+Y))² = M((X-MX) + (Y-MY))² = = M(X-MX)² + 2M(X-MX) M(Y-MY) + M(Y-MY)² = | M(X-MX) = MX - MX = 0 | = DX + DY.

Приведем задачи вычисления дисперсии для некоторых наиболее важных случайных величин.

Задача 2.3.7. Найти дисперсию случайной величины с нормальным законом распределения.

Решение. Для случайной величины с нормальным законом распределения плотность вероятностей имеет вид f(x) =

Поэтому с учетом формулы (2.3.10) для дисперсии имеем

DX = (x-MX)²f(x)dx = = =

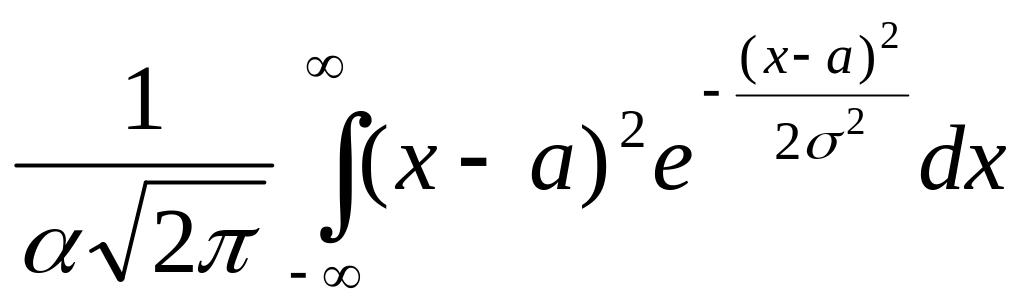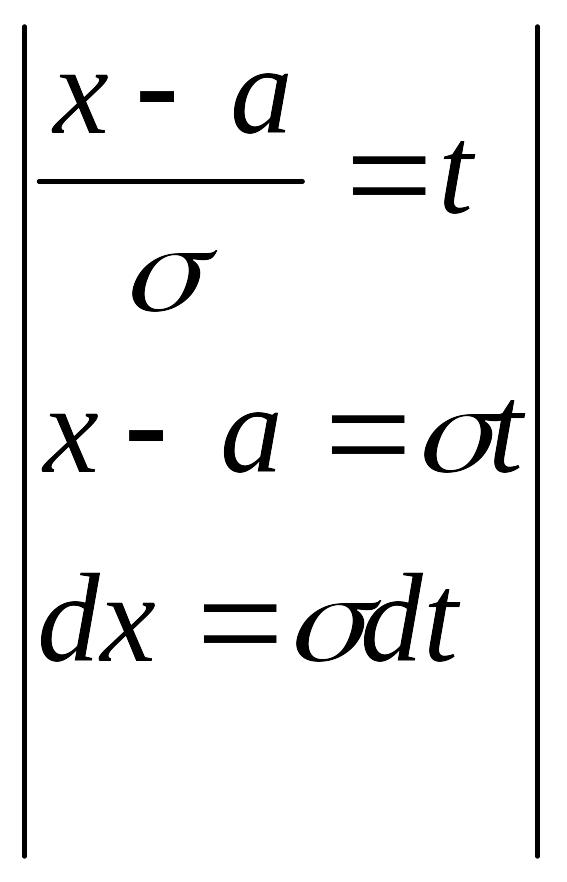= = , т.е. DX = .

Задача 2.3.8. Найти дисперсию случайной величины с биномиальным законом распределения.

Решение. Для этой случайной величины X – число ''успехов'' в n испытаниях Бернулли. В задаче 2.3.2 показано, что МХ = np. Найдем DX. Введем следующие случайные величины: Х₁ – число ''успехов'' в 1-м испытании; Х₂ – число ''успехов'' во 2-м испытании и т.д. Х_n – число ''успехов'' в n-м испытании.

Тогда Х = Х₁ + Х₂ + ... + Х_n и DX = DX₁ + DX₂ + ... + DX_n.

Найдем математическое ожидание и дисперсию любого из слагаемых, например, Х₁. Имеем

Х1	0	1	MX = 0 q + 1  p = p, DX1 = (0 - p)2 q + (1 - p)2p = p2q + q2p = pq(p +q) = pq.
Р	q	p

Тогда DX = npq .

Задача 2.3.9. Найти дисперсию случайной величины, распределенной по закону Пуассона.

Можно показать, что DX = .

Кроме центрального момента второго порядка, в теории вероятностей применяются центральные моменты третьего и четвертого порядков.

Центральный момент третьего порядка µ₃ служит характеристикой асимметрии (''скошенности'') распределения. Так как µ₃ имеет размерность куба случайной величины, рассматривают отношение µ₃ к среднему квадратическому отклонению в третьей степени .

Величина a_x называется коэффициентом асимметрии. Если кривая распределения ”скошена” влево, a_x > 0; если ''скошена'' вправо – a_x < 0.

Если µ₃ = 0 кривая распределения симметрична относительно своего математического ожидания, то a_x = 0.

Центральный момент четвертого порядка μ₄ служит для характеристики островершинности или плосковершинности распределения. Это свойство распределения описывается с помощью так называемого эксцесса. Эксцессом случайной величины Х называется величина 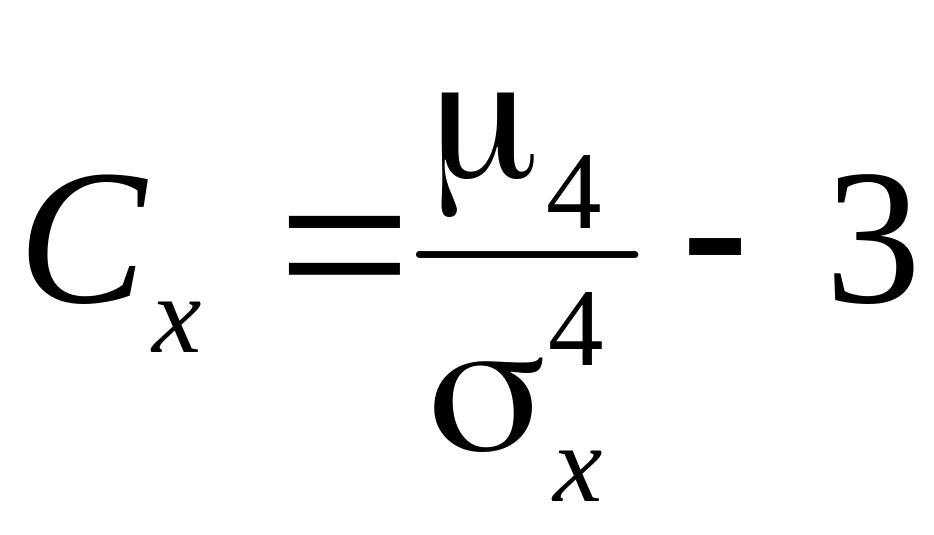. Число 3 вычитается из отношения , так как для наиболее распространенного нормального закона распределения , а, следовательно, C_x = 0; кривая нормального распределения принята в качестве эталона. Кривые более островершинные имеют положительный эксцесс; кривые более плосковершинные — отрицательный эксцесс.