А.А. Афонин

ТЕОРИЯ ВЕРОЯТНОСТЕЙ МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

СЛУЧАЙНЫЕ ПРОЦЕССЫ

Учебное пособие

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Таганрогский государственный радиотехнический университет

А.А. Афонин

ТЕОРИЯ ВЕРОЯТНОСТЕЙ МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

СЛУЧАЙНЫЕ ПРОЦЕССЫ

Учебное пособие

Таганрог 2005

УДК 511

Афонин А.А. Теория вероятностей. Математическая статистика. Случайные процессы: Учебное пособие. – Таганрог : Изд-во ТРТУ, 2004. – 135 с.

Учебное пособие написано на основе лекций, прочитанных автором на протяжении ряда лет студентам экономических и гуманитарных специальностей ТРТУ. Учебное пособие содержит теоретический материал по теории вероятностей, математической статистике и случайным процессам (в основном, процессам Маркова) с приложением к теории массового обслуживания, изложенный на достаточно строгом научном уровне и соответствующий образовательным стандартам этих специальностей. Учебное пособие содержит дополнительный материал, необходимый для понимания изложенного, а также множество содержательных примеров и задач. В конце каждого раздела приведены вопросы для самопроверки и задачи для решения с ответами; завершается учебное пособие двумя отдельными многовариантными итоговыми контрольными работами по этой дисциплине.

Учебное пособие может быть полезно также для студентов других специальностей и форм обучения, а также аспирантам и преподавателям, ведущим занятия по этой дисциплине.

Библиогр. : 6 назв.

Печатается по решению редакционно-издательского совета Таганрогского государственного радиотехнического университета.

Рецензенты:

Нахушев А.М., доктор физ.-мат. наук, профессор, академик РАЕН, президент АМАН;

Грищенко О.В., канд. эконом.наук, доцент каф. бух.учета и аудита ТИУЭ.

© Таганрогский государственный радиотехнический университет, 2005

© Афонин А.А., 2005

Введение

В настоящее время методы теории вероятностей широко используются не только в различных отраслях естествознания и техники, но и в тех областях человеческой деятельности, где ее применение не представлялось ранее возможным – в экологии, экономике, управлении.

Теория вероятностей изучает эти области, рассматривая их в формализованном виде как результаты эксперимента со случайным исходом. Несмотря на случайный характер этих явлений, их действие проявляется в определенных закономерностях, и именно они представляют интерес для успешной деятельности людей, занятых в этих отраслях. Теория вероятностей как наука прошла большой путь от применений в азартных играх к применениям в сложнейших отраслях человеческой деятельности, какими являются экономика и управление объектами в самых разнообразных формах; некоторые ее законы являются универсальными для самых различных природных и общественных явлений.

Вероятностный подход ныне широко применяется для построения дискретных и непрерывных математических моделей для описания и анализа физических реалий – объектов, процессов, часто весьма далеких друг от друга. Вероятностные методы находят также применения в таких важных сферах управленческой деятельности, как принятие решений отдельными лицами и принятие групповых решений.

1. Случайные события и вероятность

1.1. Пространство элементарных событий. Случайные события. Алгебра событий

Пусть в эксперименте со случайным исходом указаны все элементарные исходы, удовлетворяющие следующему требованию: в результате эксперимента непременно происходит один и только один из этих исходов. Каждый такой исход называется элементарным событием и обозначается буквой ω. По смыслу элементарные события неразложимы на более простые. Множество всех элементарных событий называют пространством элементарных событий Ω. Таким образом, по определению Ω={ω}.

Всякий результат эксперимента со случайным исходом в теории вероятностей называют случайным событием. Случайные события обозначают заглавными буквами латинского алфавита: A, B, C и т. д. Случайное событие А полностью характеризуется совокупностью элементарных событий , которые влекут А. Говорят, что событие А произошло, если опыт закончился одним из элементарных исходов, входящих в событие А.

Произвольное множество А точек можно рассматривать как событие А, которое происходит или не происходит в зависимости от того, принадлежит или нет множеству А элементарное событие ω, представляющее данный исход эксперимента. Таким образом, случайным событием А называют произвольное подмножество пространства элементарных событий Ω, состоящее из точек , представляющих те элементарные события ω, при которых происходит А. Поэтому в дальнейшем не делается различий между случайным событием А и соответствующим подмножеством .

Пространство элементарных событий Ω в зависимости от числа элементарных событий в нем может быть конечным или бесконечным; в последнем случае – счетным или несчетным.

Пример 1.1.1. В случае однократного подбрасывания монеты пространство элементарных событий Ω представляет собой множество, состоящее из двух элементов: Ω={ω₁,ω₂}, где ω₁ – выпадение герба, ω₂ – выпадение решки.

Пример 1.1.2. В случае однократного бросания игральной кости пространство элементарных событий Ω представляет собой множество, состоящее из шести элементов: Ω={ω₁,ω₂,ω₃,ω₄,ω₅,ω₆}, где ω₁ – выпадение грани с «1»; ω₂ – выпадение грани с «2»; ω₃ – выпадение грани с «3»; ω₄ – выпадение грани с «4»; ω₅ – выпадение грани с «5»; ω₆ – выпадение грани с «6».

Примеры случайных событий: А – выпадение герба при однократном бросании монеты; В – выпадение четной цифры при однократном бросании игральной кости; С – выигрыш, выпавший на определенный билет лотереи; D – победа определенного кандидата на выборах; Е – падение курса акций на биржевом рынке.

Рассмотрим операции над случайными событиями и их теоретико-множественые аналоги.

Если случайное событие А происходит всякий раз, когда происходит событие В, будем говорить, что событие А является следствием В, и обозначать . Естественно, это означает, что любая точка содержится и в А, т. е. .

Как и в теории множеств, из и следует А=В. Событие называют событием, противоположным событию А; оно происходит, если не происходит А.

Если событие А не содержит ни одного элементарного события, оно называется невозможным и обозначается Ø; Ø – естественно является пустым подмножеством Ω .

Событие, противоположное невозможному событию Ø, называется достоверным событием; оно обозначается Ω и происходит всякий раз (при определенном комплексе условий).

Событие С, происходящее тогда и только тогда, когда происходят события А и В, называется произведением и обозначается АВ или .

События А и В называются несовместными, если они не могут произойти вместе, т.е. Ø.

Суммой событий А и В называется событие С, которое происходит, если происходит хотя бы одно из событий А или В; обозначают сумму или А+В (для несовместных случайных событий).

Операции сложения и умножения случайных событий, естественно, можно обобщить на случай произвольного числа событий (аналогично операциям объединения и пересечения в теории множеств): или для суммы и и для произведения.

Операции сложения и умножения случайных событий обладают следующими свойствами:

1. коммутативность, т.е. 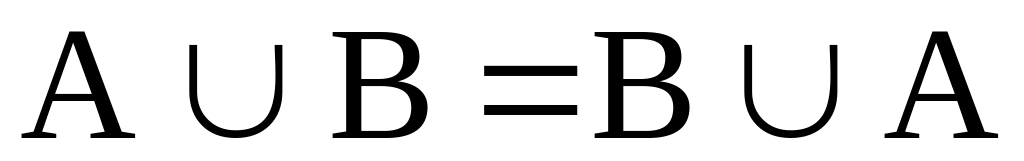и АВ=ВА;

2. ассоциативность, т.е. 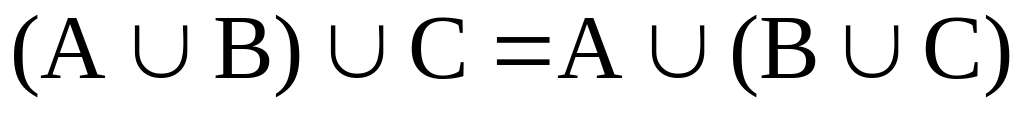и (АВ)С=А(ВС);

3. дистрибутивность, т.е. .

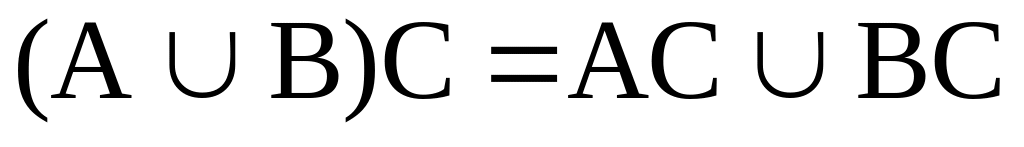Легко видеть, что событие противоположно событию АВ. Действительно, наступление хотя бы одного из событий и равносильно ненаступлению АВ, т.е.

. (1.1.1)

И вообще, для любого множества событий A_s, ,

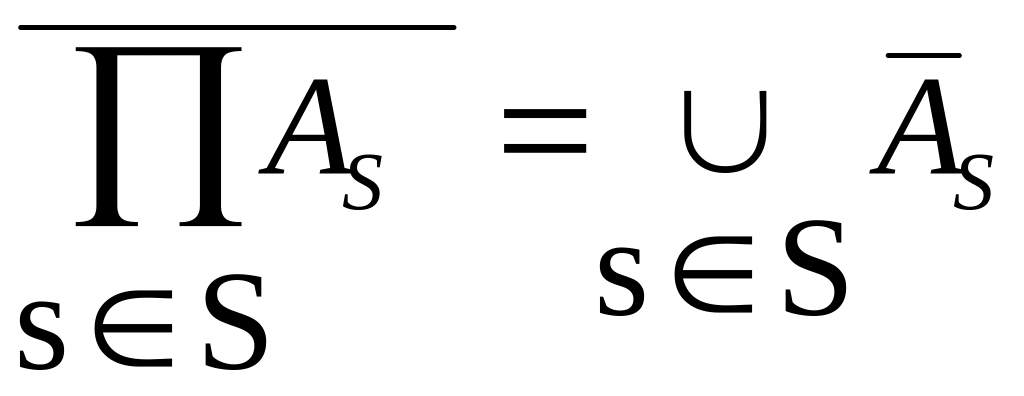. (1.1.2)

С другой стороны, событие противоположно событию , так как совместное наступление событий и равносильно ненаступлению . Поэтому

(1.1.3)

И вообще, для любого множества событий , ,

_. (1.1.4)

Формулы (1.1.1) – (1.1.4) выражают принцип двойственности для случайных событий.

Разностью событий А\В называется случайное событие, которое происходит, если происходит событие А и не происходит В.

Пусть множество всех возможных событий F удовлетворяет следующим двум условиям:

1. для любой пары событий А, имеет место включение ;

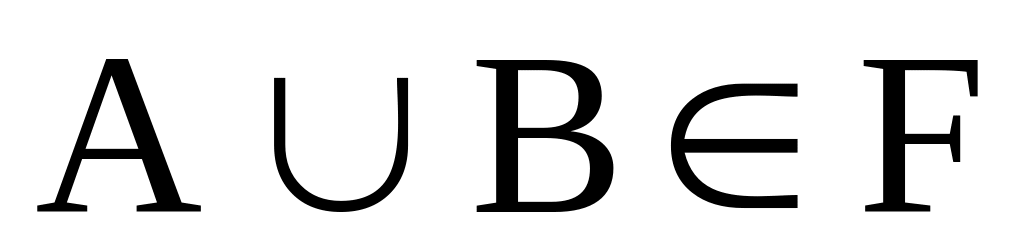2. для любого события 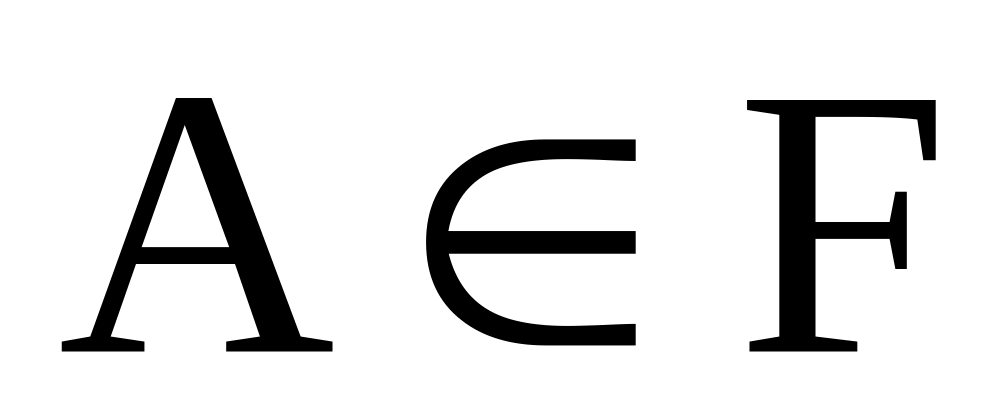имеет место включение .

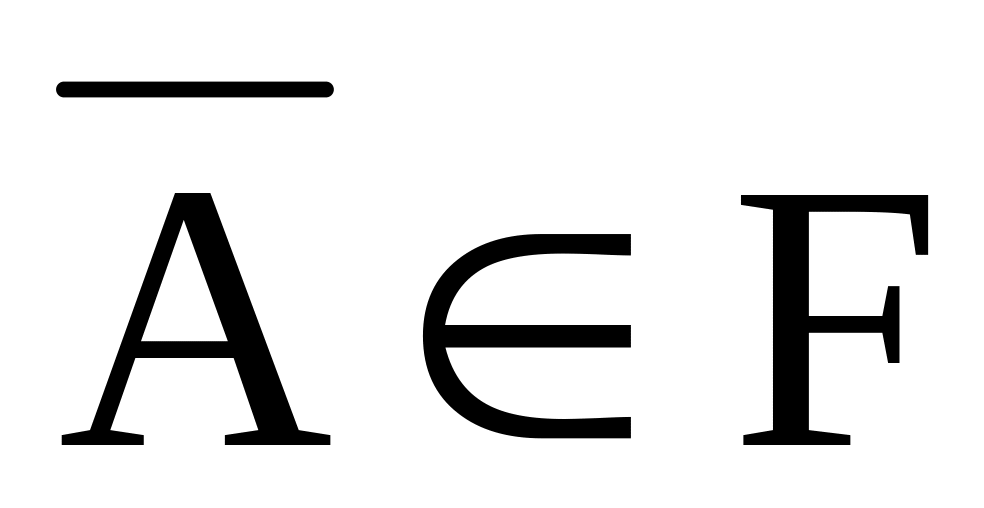Отсюда, а также из принципа двойственности, следует, что и .

Класс F случайных событий, удовлетворяющих условиям 1 и 2, называется алгеброй событий.

F состоит из всех подмножеств Ω. В случае, если Ω конечно и содержит n элементарных событий, F содержит 2ⁿ событий.