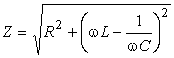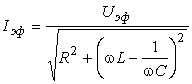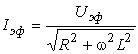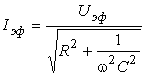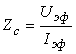Лабораторная работа № 10 определение индуктивности катушки, емкости конденсатолра и проверка закона ома для переменного тока

Под действием переменной электродвижущей силы (ЭДС) в электрической цепи, в ней возникает переменный ток.

Переменным называется такой ток, который изменяется по направлению и по величине. В данной работе рассматривается только такой переменный ток, величина которого изменяется периодически по синусоидальному закону.

Переменный ток в металлах представляет собой движение свободных электронов то в одном, то в противоположном направлении. При синусоидальном токе характер этого движения совпадает с гармоническими колебаниями. Таким образом, синусоидальный переменный ток имеет период Т  время одного полного колебания и частоту v  число полных колебаний за единицу времени. Между этими величинами имеется зависимость

,

.

Циклическая частота равна

.

Цепь переменного тока, в отличие от цепи постоянного тока, допускает включение конденсатора.

Е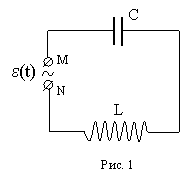 сли обкладки конденсатора присоединить к источнику постоянного тока, то в цепи пойдет быстро уменьшающийся ток, который прекратится, когда на обкладках конденсатора возникнет разность потенциалов, компенсирующая ЭДС источника тока. Если же обкладки конденсатора присоединить к источнику переменной ЭДС, то они непрерывно будут перезаряжаться, и в цепи все время будет идти ток.

Соединим последовательно конденсатор, емкость которого С, с катушкой, имеющей активное сопротивление R и индуктивность L (сопротивление проводящих проводов будем считать малым по сравнению с R); к концам этой цепи М и N(рис. 1) приложим переменную ЭДС

, (1)

где   мгновенное значение ЭДС;    максимальная (амплитудная) ЭДС;   циклическая частота переменной ЭДС; t  время.

В цепи кроме ЭДС  действует еще и ЭДС самоиндукции, равная  , где I  сила тока. Таким образом, в цепи действует полная ЭДС, равная

.

Согласно второму правилу Кирхгофа, алгебраическая сумма падений потенциала в контуре (цепи)   (U  разность потенциалов между обкладками конденсатора) равна алгебраической сумме ЭДС в контуре. Следовательно,

.

(2)

Если q  заряд конденсатора, то

.

(3)

Ток в цепи равен увеличению заряда конденсатора за единицу времени

.

(4)

Учитывая (1) и (3), из (2) получаем

.

Дифференцируя последнее уравнение по времени и учитывая (4), получим

.

(5)

Уравнение (5) представляет собой дифференциальное уравнение, решением которого является такая функция силы тока от времени I(t), при подстановке которой в (5) левая часть уравнения тождественно (для всех значений t) становится равной правой части.

Решение уравнения (5) для установившегося процесса имеет вид

, (6)

где I  мгновенное значение переменного тока;   максимальное (амплитудное) значение тока;   начальная фаза тока, причем

.

(7)

Амплитудное значение тока выражается через параметры цепи следующим образом:

.

(8)

Подставляя выражение для I из (6) в уравнение (5), можно убедиться, что (6) тождественно удовлетворит (5), если принять во внимание формулы (7) и (8).

Из (6) следует, что в цепи течет переменный ток, частота которого равна частоте приложенной ЭДС , но ток сдвинут по фазе относительно ЭДС на величину . Таким образом, в цепи устанавливаются вынужденные незатухающие колебания.

Формула (8), выражающая зависимость амплитуды тока   от амплитуды ЭДС  , по своей форме напоминает закон Ома, причем роль сопротивления играет величина

,

(9)

называемая полным сопротивлением или импедансом цепи. Поэтому выражение (8) называют законом Ома для переменного тока.

В данной работе активное сопротивление R катушки определяется при помощи закона Ома для участка цепи постоянного тока.

В полученные формулы для переменного тока входят амплитудные (максимальные) значения тока   и ЭДС  . Но амперметры и вольтметры в цепи переменного тока измеряют не амплитудные значения тока и напряжения, а эффективные (действующие) значения этих величин. Переменный ток, проходя через проводник с активным сопротивлением R, выделяет в этом проводнике за некоторый промежуток времени t определенное количество тепла. Под эффективной величиной переменного тока   понимают величину такого постоянного тока, который, проходя через то же сопротивление R, выделяет в проводнике за время t такое же количество тепла, как и переменный ток. Расчет показывает, что для синусоидальных токов

.

(10)

Аналогично определяется эффективное напряжение

,

(11)

где   амплитудное значение напряжения, а эффективная ЭДС переменного тока (12)

.

Из формул (10) и (12) следует, что

,

(13)

поэтому в формулу закона Ома для переменного тока (8) можно вместо величин   и   соответственно подставить величины   и  .

Если к точкам М и N (рис. 1) подключить вольтметр, то он практически покажет  , если сопротивление источника переменной ЭДС мало по сравнению с сопротивлением внешнего участка цепи. Если же сопротивление источника ЭДС велико, то подключенный к точкам М и N вольтметр покажет падение напряжения   на внешней цепи. В соответствии с изложенным, закон Ома для переменного тока получит вид

.

(14)

Рассмотрим два частных случая.

1. В цепи отсутствует конденсатор. Это значит, что конденсатор отключается и вместо него цепь замыкается проводником, падение потенциала на котором практически равно нулю, то есть величина U в уравнении (2) равна нулю. Условие   удовлетворяется, если во всех выражениях, содержащих величину С, перейти к пределу  .

При   из формул (6), (7), (9) и (14) соответственно получаем

, (15)

,

(16)

,

(17)

,

(18)

где    полное сопротивление цепи при отсутствии в ней конденсатора. Величина   называется индуктивным сопротивлением. Из сопоставления уравнений (1) и (15) следует, что ток отстает по фазе от напряжения, то есть фаза тока на величину  меньше фазы напряжения.

Из (17) и (18) получаем

,

(19)

.

(20)

2. В цепи отсутствует катушка: следовательно  .

При   из формул (6), (7) и (14) соответственно имеем

, (21)

,

(22)

.

(20)

Из сопоставления уравнений (1) и (21) следует, что ток опережает напряжение по фазе на величину , т.е. фаза тока больше фазы напряжений.

Считая активное сопротивление R соединительных проводов малым по сравнению с общим сопротивлением цепи  , из формулы (9) получаем

,

(24)

где    общее сопротивление цепи при L = 0 и R = 0. Величина   называется емкостным сопротивлением.

Из (23) при R = 0 имеем

,

(25)

а из (24) получаем

.

(26)

Следует отметить, что при   из (22) имеем  . Это значит, что  , то есть в данном случае ток опережает напряжение по фазу на  .

Сопротивления   так же как и активное сопротивлениеR, в системе СИ выражается в Омах.