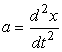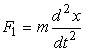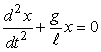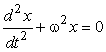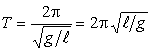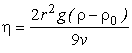Лабораторная работа № 2 определение ускорения свободного падения при помощи модели математического маятника

Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити

В вертикальном положении сила тяжести Р шарика полностью уравновешивается натяжением нити Т, и маятник остается в покое. Это положение называется положением равновесия (точка А).

Таким образом, колебания маятника, совершаемые под действием силы  , характеризуются величинами х, х₀ и Т. Найдем математическое выражение, объединяющее эти величины.

Из рис. 1 видно, что

, (2)

где

.

(3)

Подставляя (3) в (2), получим

.

(4)

Знак "минус" в формуле (4) означает, что сила   и смещение х всегда направлены в разные стороны.

Сила  , согласно второму закону Ньютона, равна

. (5)

Ускорение а равно второй производной смещения х по времени

t:

, тогда

.

(6)

Из (4) и (6) получаем

и, следовательно,

.

(7)

Так как величины  и   положительные, то их отношение можно приравнять к квадрату некоторой величины

.

(8)

Подставляя (8) в (7), получим

.

(9)

Выражение (9) является дифференциальным уравнением гармонических колебаний. Частным решением этого уравнения является функция

,

(10)

где t  текущее время или время начала отсчета;    фаза колебаний;    начальная фаза, т.е. фаза, соответствующая отклонению маятника в момент времени  ;  круговая (циклическая) частота.

Величина   (амплитуда) и   в (10) не зависят от t. Колебания будут гармоническими, если зависимость смещения х от времени t будет выражаться через функции sin и cos; следовательно, уравнение (10) есть уравнение гармонических колебаний.

Одним из свойств гармонических колебаний является то, что любое положение маятника (или какое-либо значение гармонической функции) точно повторяется через время Т, за которое фаза   получает приращение  . Таким образом, если ко времени T прибавить время одного полного колебания, то фаза изменится на 

. (11)

Раскрыв скобки в (11) и приводя сокращения, получим

.

(12)

Время Т связано с частотой колебания f соотношением

.

(13)

Из (12) и (13) следует, что

, (14)

где f  число полных колебаний в единицу времени.

Для нахождения ускорения свободного падения g подставим в (12) значение   из (8)

,

(15)

откуда

.

(16)

Лабораторная работа № 4 определение динамической вязкости жидкости по методу стокса

В реальных жидкостях молекулы расположены относительно друг друга очень близко и между молекулами возникает сила притяжения. При движении жидкости эти силы притяжения проявляются в виде сил внутреннего трения в жидкости. Это свойство жидкости называется вязкостью. Явление вязкости заключается в том, что возникшее в жидкости движение после прекращения действия причин его вызвавших, постепенно прекращается. Если время прекращения такого движения очень мало, то говорят, что вязкость жидкости очень большая и наоборот.

Силы притяжения между молекулами жидкости называются когезионными, а силы притяжения, действующие между молекулами жидкости и стенками сосуда, в котором находится жидкость, адгезионными.

Ч тобы получить меру вязкости жидкости, рассмотрим слой жидкости между двумя большими параллельными пластинами (рис. 1), которые смачиваются этой жидкостью. Явление смачивания возникает тогда, когда адгезионные силы больше когезионных.

Рассмотрим относительное движение твердотельных пластин в вязкой жидкости, разделенных слоем жидкости толщиной d. Нижняя пластина А неподвижна. Что произойдет, когда верхняя пластина В начнет равномерно двигаться со скоростью v под действием постоянной силы F? Жидкость смачивает пластины, а это значит, что слой, непосредственно прилегающий к пластине В, тоже будет двигаться со скоростью v.

Из-за сил внутреннего трения (вязкости) этот слой влияет на слой, лежащий непосредственно под ним, заставляя его двигаться, но со скоростью  , немного меньшей, чем v. Каждый слой передает движение с меньшей скоростью слою, лежащему под ним, и так до неподвижного нижнего слоя, прилегающего к пластине А. Если скорость v достаточно мала, эта передача движения заставляет каждый слой двигаться гладко; траектория движения каждой частицы жидкости прямолинейна. Такой тип движения называется ламинарным.

Пластина движется равномерно, под действием силы F. Это значит, что действие силы F уравновешивается равной ей по величине и противоположно направленной силой трения жидкости  .



. (1)

Для того чтобы выражение (1) записать в виде формулы, надо ввести коэффициент пропорциональности  , который называется динамической вязкостью

.

(2)

В 1687 г. Ньютон вывел закон вязкого течения

(3)

где   и   скорости слоев жидкости, расстояние между которыми равна   (см. рис.1); S  площадь слоев жидкости, по которым происходит сдвиг (изменение скорости), а   градиент скорости (быстрота изменения скорости в выбранном направлении в пространстве).

Коэффициент пропорциональности   (динамическая вязкость) определяет сопротивление движению тела в вязкой среде. Динамическая вязкость зависит от природы среды, она изменяется с температурой. Для жидкостей вязкость фактически уменьшается с ростом температуры. Динамическая вязкость численно равна силе, действующей на единицу площади поверхности, находящейся в движущейся среде, в которой градиент скорости равен единице.

Из (2)

(4)

Выражение (4) определяет единицу вязкости. В СИ   есть давление, и выражается в Паскалях, а   в знаменателе выражается в с^-1.

Па с.

В СГС   выражается в единицах Пуаз (П)

1 Па с = 10 П.

В методе Стокса динамическая вязкость жидкости определяется при падении шарика в жидкости. При движении тела в вязкой жидкости возникают силы сопротивления. При небольших скоростях движения, когда жидкость спокойно обтекает тело, за ним (телом) не образуется вихрей (ламинарное течение), слои жидкости, прилегающие к телу, увлекаются им, и между этими слоями возникают силы трения.

Если скорость движения большая, то ламинарность движения обтекающей тело жидкости нарушается, за телом образуются вихри, давление позади шарика уменьшается и возникает дополнительная сила, препятствующая движению тела.

При движении шарика в вязкой жидкости с небольшой скоростью, сила сопротивления движению шарика определяется по закону Стокса

,

(6)

где r  радиус шарика; v  скорость его движения;   динамическая вязкость жидкости.

На шарик, движущийся в жидкости, действуют три силы (см. рис. 2): сила сопротивления  ; выталкивающая сила (сила Архимеда)  ; сила тяжести  .

,

(7)

,

(8)

г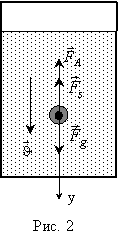 де    плотность шарика;    плотность жидкости.

Сила тяжести и выталкивающая сила постоянны по модулю, не меняются, а сила сопротивления среды изменяется: она зависит от скорости движения тела: чем больше скорость, тем больше сила сопротивления среды.

Рассмотрим теперь движение шарика при выполнении данной работы. Шарик бросается в цилиндр с вязкой жидкостью с некоторой высоты h. От точки бросания до поверхности жидкости шарик движется под действием силы тяжести с ускорением, равным g (сопротивление воздуха не учитывается). При попадании в жидкость скорость шарика оказывается большой и, следовательно, сила сопротивления среды также имеет большое значение. Под действием этой силы сопротивления среды скорость шарика уменьшается и наступает момент, когда скорость шарика становится постоянной, то есть равнодействующая всех трех сил становится равной нулю. При равномерном движении шарика сумма сил   и  , направленная вверх, по модулю равна силе Р, направленной вниз

. (9)

Подставляя в (9) значения Р,   и   из (6), (7), (8), найдем из этого уравнения коэффициент вязкости

.

(10)