
Теоретический минимум ЯМП
.docx1.1. Язык
Формальным языком называется любое множество строк (в данном алфавите Σ)
Строка – упорядоченная конечная последовательность символов алфавита Σ. Алфавит – это конечное непустое множество символов Σ = {a1, a2, a3, ... , an}, n>0.
1.2. Грамматика
Грамматикой G называется следующая упорядоченная четверка объектов G = (N, T, S, P), где
N – конечное множество нетерминальных символов, называемых переменными (или нетерминалами);
T – конечное множество терминальных символов, называемых терминалами; S – начальный символ, S ∈ N;
P – конечное множество правил вывода, называемых продукциями. Здесь и далее предполагается, что множества N и Т непустые и не пересекаются.
1.3. Язык, порождаемый грамматикой
Пусть G = (N, T, S, P) –
грамматика. Тогда множество L(G) = {α | α ∈
T* и S
![]() α} называется языком, порождаемым
грамматикой G.
α} называется языком, порождаемым
грамматикой G.
1.4. Эквивалентные грамматики
Две грамматики G1 и G2 называются эквивалентными, если они порождают один и тот же язык, т.е. если L(G1) = L(G2).
1.5. Детерминированный конечный автомат
Детерминированный конечный автомат (распознаватель), или сокращенно ДКА, – это пятерка M = (Q, Σ, θ, q0, F), где: Q – конечное множество внутренних состояний; Σ – конечное множество символов, называемое входным алфавитом; θ: Q × Σ → Q – всюду определенная функция, называемая функцией переходов; q0 ∈ Q – начальное состояние; F ⊆ Q – множество заключительных состояний.
1.6. Диаграмма переходов
Диаграмма переходов - ориентированные конечные графы, в которых вершины соответствуют внутренним состояниям автомата (и помечаются соответствующими символами).
1.7. Язык, допустимый ДКА
Язык, допустимый ДКА M = (Q, Σ, θ, q0, F), – это множество всех строк из Σ*, допустимых автоматом М, т.е. L(M) = {α | α ∈ Σ* и θ*(q0, α) ∈ F}.
1.8. Автоматный язык
Пусть p – регулярное выражение. Тогда существует некоторый недетерминированный конечный автомат M(p), который допускает язык L(p), т.е. L(p) – автоматный язык.
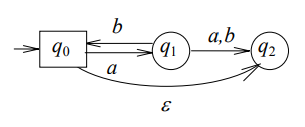
1.9. Недетерминированный конечный автомат
Недетерминированный конечный автомат (распознаватель), или НКА, – это пятерка М = (Q, Σ, θ, q0, F), где Q, Σ, q0, F определяются так же, как и для ДКА, а функция переходов θ выглядит так:
θ: Q × (Σ ∪ {ε}) → 2Q
1.10. Эквивалентность автоматов
Два автомата эквивалентны, если они допускают один и тот же язык.
1.11. Регулярное множество
Пусть Σ – конечный алфавит. Регулярное множество в алфавите Σ определяется рекурсивно следующим образом:
1. Пустое множество ∅ – регулярное. 2. Множество {ε} – регулярное. 3. Для любого a ∈ Σ множество {a} – регулярное (в алфавите Σ). 4. Если P и Q – регулярные множества в алфавите Σ, то регулярными являются и множества P ∪ Q, P Q, P*. 5. Других регулярных множеств в алфавите Σ нет.
Итак, множество в алфавите Σ регулярно тогда и только тогда, когда оно либо ∅, либо {ε}, либо {a}, где a ∈ Σ, либо получено из этих множеств применением конечного числа операций объединения, сцепления и итерации.
1.12. Регулярное выражение
Регулярные выражения в алфавите Σ и обозначаемые ими регулярные множества в том же алфавите определяются рекурсивно следующим образом:
1. φ – регулярное выражение, обозначающее регулярное множество ∅. 2. e – регулярное выражение, обозначающее регулярное множество {ε}. 3. Если а ∈ Σ, то а – регулярное выражение, обозначающее регулярное множество {a}. 4. Если p и q – регулярные выражения, обозначающие регулярные множества L(p) и L(q), то (p + q) – регулярное выражение, обозначающее регулярное множество L(p) ∪ L(q); (p • q) – L(p)L(q); (р)* – (L(p))*. 5. Других регулярных выражений в алфавите Σ нет. Учитывая наше соглашение относительно приоритетов операций +, • и *, мы будем избегать употребления избыточных скобок в регулярных выражениях. Например, запись a + b•a* означает выражение (a + (b•(a*))).
1.13. Эквивалентность регулярных выражений
Регулярные выражения p и q эквивалентны, если L(p) = L(q), т.е. если они обозначают одно и то же множество. Будем в этом случае писать p = q.
1.14. Праволинейная грамматика
Грамматика G = (N, T, S, P) называется праволинейной, если все продукции имеют вид A → α B A → α , где А, В ∈ N, α ∈ T*
1.15. Леволинейная грамматика
Аналогично грамматика называется леволинейной, если все продукции имеют вид A → B α A → α.
1.16. Регулярная грамматика
Грамматика называется регулярной, если она или праволинейная, или леволинейная
1.17. Регулярный язык
Язык назовем регулярным, если он порождается некоторой регулярной грамматикой.
1.18. КС-грамматики
Грамматика G = (N, T, S, P) называется контекстно-свободной (или КС-грамматикой), если любая ее продукция имеет вид А → α, где А ∈ N, α ∈ (N ∪ T)*.
1.19. КС-язык
Язык L называется контекстно-свободным (или КС-языком), если существует контекстно-свободная грамматика G такая, что L = L(G). Так как, очевидно, любая регулярная грамматика контекстно-свободна, то и любой регулярный язык является КС-языком.
1.20. Левосторонний и правосторонний вывод в КС-грамматике
Вывод в КС-грамматике называется левосторонним, если на каждом шаге замещается самый левый нетерминальный символ. Если замещается всегда самый правый символ, то вывод называется правосторонним.
1.21. Дерево вывода в КС-грамматике
Упорядоченное дерево, вершины которого помечены левыми частями продукций, а непосредственные потомки вершины в совокупности представляют собою правую часть соответствующей продукции. Так, если на некотором шаге вывода в грамматике G = (N, T, S, P) была применена продукция X → Y1Y2 ... Ym, а затем продукция Y2 → Z1Z2 ... Zn, где Yi, Zi ∈ N ∪ T, 1 ≤ i ≤ m, 1 ≤ j ≤ n, Y2 ∈ N,
1.22. Нормальная форма Хомского
КС-грамматика G = (N, T, S, P) имеет нормальную форму Хомского, если любая ее продукция имеет вид либо A → BC, либо A → a, где A, B, C ∈ N, a ∈ T.
1.23. Нормальная форма Грейбах
КС-грамматика G = (N, T, S, P) имеет нормальную форму Грейбах, если все ее продукции имеют вид A → aα, где A ∈ N, a ∈ T, α ∈ N*. Заметим, что, в силу определения, грамматика в нормальной форме Грейбах не может быть леворекурсивной.
2. Алгоритмы преобразования грамматик
2.1. Удаление eps-продукций
1. Добавить все правила из P в P′.
2. Найти все ε-порождающие нетерминалы.
3. Для каждого правила вида A→α0B1α1B2α2…Bkαk (где αi — последовательности из терминалов и нетерминалов, Bj — ε-порождающие нетерминалы) добавить в P′ все возможные варианты правил, в которых либо присутствует, либо удалён каждый из нетерминалов Bj(1⩽j⩽k).
4. Удалить все ε-правила из P′.
5. Если в исходной грамматике Γ выводилось ε, то необходимо добавить новый нетерминал
S′, сделать его стартовым, добавить правило S′→S|ε.
2.2. Удаление цепных продукций
Шаг 1. i=0, P0'={A→α ∈ P и (|α|>1) или (|α|=1 и VT)}, где α — последовательность символов.
Шаг 2. i=i+1, Pi' = Pi - 1'{X →, где XRA + все правила A → Pi - 1'}.
Шаг 3. Если Pi' Pi - 1' тогда повторяется шаг 2
Шаг 4. Если Pi' = Pi - 1' тогда стоп.
2.3. Удаление бесполезных нетерминалов и продукций
Шаг 0. Множество порождающих нетерминалов пустое.
Шаг 1. Находим правила, не содержащие нетерминалов в правых частях и добавляем нетерминалы, встречающихся в левых частях таких правил, в множество.
Шаг 2. Если найдено такое правило, что все нетерминалы, стоящие в его правой части, уже входят в множество, то добавим в множество нетерминалы, стоящие в его левой части.
Шаг 3. Повторим предыдущий шаг, если множество порождающих нетерминалов изменилось.
В результате получаем множество всех порождающих нетерминалов грамматики, а все нетерминалы, не попавшие в него, являются непорождающими.
2.4. Удаление недостижимых нетерминалов

2.5. Удаление левой рекурсии
Опишем процедуру, устраняющую все правила вида A→Aα, для фиксированного нетерминала A.
-
Запишем все правила вывода из А в виде А → Aα1 | ... | Aαn | β1| … | βm, где α - непустая последовательность терминалов и нетерминалов (α ↛ eps) β - непустая последовательность терминалов и нетерминалов, не начинающихся с А.
-
Заменим правила вывода из А на А → β1А’| … | βmA’| β1| … | βm.
-
Создадим новый терминал А’ → α1A’ | … | αnA’ | α1| …| αn
2.6. Приведение к НФХ
Рассмотрим контекстно-свободную грамматику Г. Для приведения её к нормальной форме Хомского необходимо выполнить пять шагов. На каждом мы строим новую Гi, которая допускает тот же язык, что и Г.
-
Уберём длинные правила. Воспользуемся алгоритмом удаления длинных правил из грамматики. Получим грамматику Г1, эквивалентную исходной, содержащую правила длины 0, 1 и 2.
-
Удаление eps-правил. Воспользуемся алгоритмом удаления eps-правил из грамматики. Получим грамматику, эквивалентную исходной но в которой нет eps-правил.
-
Удаление цепных правил. Воспользуемся алгоритмом удаления цепных правил из грамматики. Алгоритм работает таким образом, что новые eps-правила не образуются. Получим грамматику Г3, эквивалентную Г.
-
Удалим бесполезные символы. Воспользуемся алгоритмом удаления бесполезных символов из грамматики. Так как Г3, эквивалентна Г, то бесполезные символы не могли перестать быть бесполезными. Более того, мы только удаляем правила, новые eps-правила и цепные правила не могли появиться.
-
Уберём ситуации, когда в правиле встречаются несколько терминалов. Для всех правил вида A → u1u2 (где ui - терминал или нетерминал) заменим все терминалы ui на новые нетерминалы правила Ui → ui. Теперь правила содержат либо одиночный терминал, либо строку из двух нетерминалов.
