1. Кинетостатический расчет механизма методом планов

Задачи кинетостатического расчета: определение реакций в кинематических парах; определение уравновешивающей силы ( ) или уравновешивающего момента ( ).

Метод базируется на принципах механики – принципе Даламбера и принципе заменяемости связей.

Порядок расчета определяется формулой строения механизма [1-3]. Расчет проводят по структурным группам, начиная с наиболее удаленной от исходного механизма, и заканчивают расчетом исходного механизма.

Более подробно познакомимся с методикой силового расчета на конкретном примере, в частности, на примере четырехзвенного кривошипно-ползунного механизма (рис. 1). В соответствии с принципом Ассура этот механизм можно представить как совокупность двух простейших кинематических цепей: исходного механизма, состоящего из звеньев 0 и 1, и структурной группы II класса 2 порядка 2 вида, состоящей из шатуна и ползуна. С определения сил, действующих на звенья структурной группы и в ее подвижных соединениях, начинается кинетостатический анализ.

Рис. 1

Исходными данными для расчета являются: кинематическая схема; все кинематические размеры; массы звеньев m₁, m₂, m₃; положения центров масс S₁ и S₂ кривошипа и шатуна; ускорения а_А, а_В, а_S1, а_S2; угловое ускорение ε₂ шатуна; диаграмма сил полезного сопротивления (рис. 2) и ее максимальное значение Р.

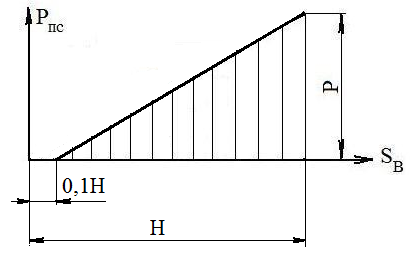
Рис. 2

2. Силовой расчет структурной группы

Расчет начинается с определения внешних сил, действующих на звенья, входящие в структурную группу. К ним относятся силы тяжести G₂ и G₃ шатуна и ползуна, силы инерции, сила полезного сопротивления Р_ПС.

• Сила тяжести i-го звена (при i = 2, 3) вычисляется по формуле [1-3]

,

где m_i - масса i-го звена; g – ускорение свободного падения, g = 9,8 м/с².

Тогда сила тяжести шатуна , сила тяжести ползуна .

• На стадии схемного проектирования, когда нет полной информации о конструкции звеньев, их размерах, материалах, из которых они изготовлены, для определения сил инерции целесообразно использовать инженерный метод, называемый методом замещающих точечных масс [1]. Суть его состоит в том, что звено заменяют системой точечных масс, расположенных в определенных точках, называемых замещающими. Расчет сил инерции звена сводится к определению сил инерции этих точечных масс. При статической замене звено заменяется двумя массами, расположенными в центрах шарниров. Так шатун заменяется двумя точечными массами m_А2 и m_В2, расположенными в центрах шарниров А и В и равными:

; .

Силы инерции замещающих масс [1-3]:

; .

Сила инерции ползуна

.

• Для определения силы полезного сопротивления Р_псj в рассматриваемом j–м положении механизма над разметкой (или под ней) строится диаграмма сил полезного сопротивления. Ось абсцисс диаграммы параллельна направляющей t-t ползуна (рис. 3), начало ее системы координат должно соответствовать началу рабочего хода механизма, т.е. точке В₀ на разметке. Ось ординат направлена перпендикулярно t-t. Отрезок В₀В₆ на разметке в масштабе μ_l изображает ход Н ползуна.

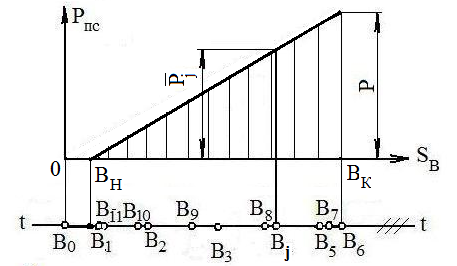
Рис. 3

В соответствии с исходными данными сила полезного сопротивления действует на большей части рабочего хода (на рис. 3 это участок В_НВ_К оси абсцисс). Во время холостого хода сила полезного сопротивления принята равной нулю.

Длина отрезка 0В_Н вычисляется по формуле

.

На оси абсцисс от начала координат откладываем отрезки 0В_Н и В_НВ_К, получим точки В_Н и В_К начала и конца действия силы полезного сопротивления соответственно. В точке В_К сила полезного сопротивления имеет максимальное значение Р. Выбираем длину отрезка , которым сила Р будет изображаться на диаграмме. Строим диаграмму.

Масштабный коэффициент μ_Р диаграммы Р_пс(S_В) вычисляется по формуле

.

Для определения значения Р_псj силы полезного сопротивления в расчетном j-м положении механизма из точки В_j на траектории движения ползуна (рис. 3) восстанавливаем перпендикуляр к оси t-t до пересечения с графиком Р_пс(S_В). Измеряем ординату в миллиметрах. Величина силы полезного сопротивления вычисляется по формуле

.

• Расчет реакций в кинематических парах начинается с составления схемы нагружения структурной группы (рис. 4). Структурная группа изображается в масштабе μ_l в расчетном ее положении. К ее звеньям прикладываются силы: полезного сопротивления Р_ПСj; тяжести G₂ и G₃; инерции Р_ИА2, Р_ИВ2, Р_И3; реакции связей R₁₂, R₀₃. На схеме нагружения силы изображаются отрезками произвольной длины, но строго выдерживается их направление. Линия действия реакции R₀₃ направлена перпендикулярно направляющей t-t ползуна. Направление и величина реакции R₁₂ неизвестны.

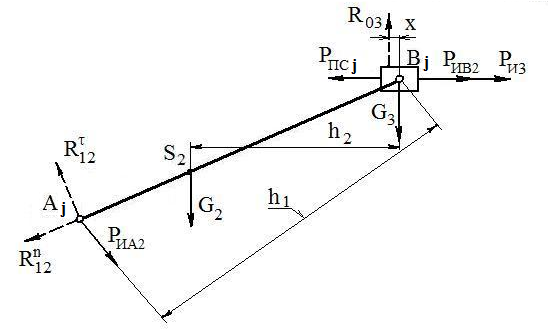
Рис. 4. Схема нагружения структурной группы

Раскладываем реакцию R₁₂ на составляющие: нормальную и тангенциальную . Составляющая направлена вдоль шатуна, а - перпендикулярно АВ. Сила инерции Р_ИА2 приложена в точке А шатуна и направлена противоположно ускорению а_А точки А, силы Р_ИВ2 и Р_И3 направлены противоположно ускорению а_В точки В шатуна. Сила Р_ИВ2 приложена в точке В шатуна, а Р_И3 - в точке В ползуна. Силы тяжести G₂ и G₃ приложены в центрах масс звеньев и направлены вертикально вниз. Сила Р_псj действует на ползун и направлена противоположно его скорости V_В.

Под действием указанной системы сил структурная группа находится в равновесии. В равновесии находится и каждое звено этой группы. Реакция определяется по условию равновесия системы сил, действующих на шатун:

.

Плечи сил измеряются в мм на схеме нагружения.

.

Знак реакции свидетельствует о том, что ее направление соответствует указанному на схеме нагружения.

Условие равновесия системы сил, действующих на структурную группу:

. (1)

Графическое решение уравнения (1) приведено на рис. 5.

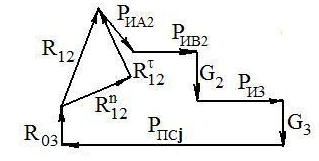
Рис. 5. План сил

Масштабный коэффициент плана сил:

,

где - длина отрезка, которым сила полезного сопротивления изображается на плане сил.

Точку приложения реакции определяем по условию равновесия системы сил, действующих на ползун. Линии действия сил Р_ПСj, G₃, Р_ИА2, Р_И3 проходят через геометрическую ось шарнира В (рис. 4). В связ с этим

.

Реакция не равна нулю, следовательно, размер . Таким образом, при центральном расположении шарнира В на ползуне линия действия реакции проходит через его геометрический центр.