Файл-процедура для нечеткой логики: определяет максимум
function [L2,i,ymax2,xmax2,t2]=findmax_fz(i,Fx,Fy);
% Вызов файла-процедуры для нахождения локального максимума
% (ymax2,xmax2) - koordinatu '2-go' lokalnogo max
% L2 - gipotenyza '2-go' treygolnika
% t2 - ygol naklona krivou
% Fx,Fy - issledyemue to4ki massiva(razdelennue na abscusu i ordinatu),
% poly4ennue iz zagrygaemux faulov s krivumi
cnt=i; %начало выполнения функции
fl=0; %flag max
%станет равно 1 когда найдется максимум
DX=Fx(2)-Fx(1); %priras4enie
Yd=[]; %sozdaem massiv dlya xraneniya zna4eniu proizvodnou
Yd=diff(Fy)/DX; %opredelenie proizvodnou
while fl==0 %vupolnyat, poka flag max = '0'
if and(Yd(i)>=0,Yd(i+1)<0)==1 %esli proizvodnaya v i-u to4ke >0
%(t.e. f-ya vozrastaet) i
%proizvodnaya
% v (i+1)-u to4ke <0(t.e. f-ya
% ybuvaet),to
xmax2=Fx(i); %zapomnit zna4enie ots4eta
ymax2=Fy(i); %i veli4inu (t.e. koordinatu
%t.(kon2,pmax2))
fl=1; %ystanovit flag max=1
end;
i=i+1; %priras4enie s4et4ika
end;
i=i-1; %vozvrat na wag(4tobu zafiksirovat t. max)
L2=sqrt((ymax2-Fy(cnt))^2+((xmax2-Fx(cnt))/20000)^2);%pas4et
%gipotenyzu(delim
%na 20000 dlya sootnoweniya
%razmernosteu)
t21=acos((xmax2-Fx(cnt))/(20000*L2)); %ras4et ygla(v radianax)
t2=180*t21/pi; %ras4et ygla(v gradysax)
Файлы-процедуры для нахождения локального минимума, для нахождения точки конца кристаллизации и остальных точек указаны в п. 7.1.2
7.3 Результаты работы программы для обнаружения границ фаз в термическом анализаторе алюминиевых сплавов при помощи нечеткой логики.
Результаты работы программы для разных участков кривой представлены на рисунках 7.6-7.10.
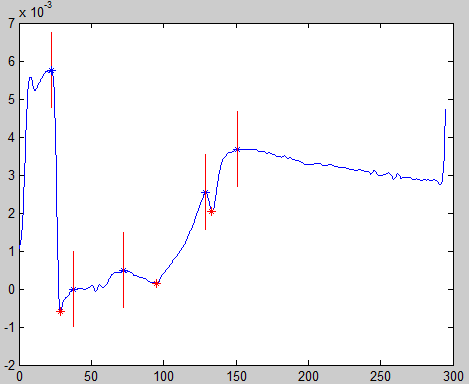
Рисунок 7.6 – Участок кривой №11 Рисунок 7.7 – Участок кривой №12
Рисунок 7.8 – Участок кривой №13 Рисунок 7.10 – Участок кривой №40
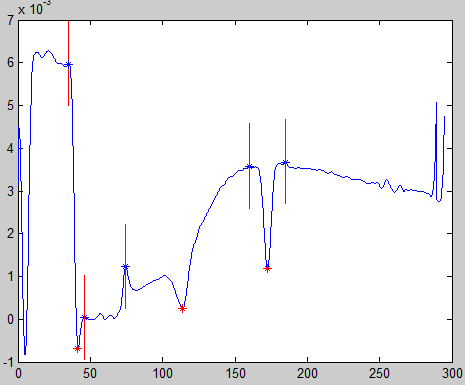
Рисунок 7.9 – Участок кривой №39
Файл-сценарий для создания снв и сохранения ее на диске в виде файла
Используя данные о диапазоне изменения значений входных и выходных параметров, границы и тип ФП, правила, веса правил и метод дефазификации, изложенные в п. 1.4, пишем программу в виде файла-сценария для создания СНВ и сохранения ее на диске в виде файла.
script;
k = 1+0.15;
k1 = 1+0.05;
a = newfis('Fis_lab_fz');
a = addvar(a,'input','L1',[0 0.0065]);
a=addmf(a,'input',1,'small','trapmf',[0 0 0.00009*k*(1+0.035) 0.00011*k*(1+0.035)]);
a=addmf(a,'input',1,'mid_left','trimf',[0.00009*k1*(1+0.035) 0.000295*k1*(1+0.035) 0.0005*k1*(1+0.035)]);
a=addmf(a,'input',1,'mid_rig','trimf',[0.0004*k*(1+0.035) 0.0007*k*(1+0.035) 0.001*k*(1+0.035)]);
a=addmf(a,'input',1,'big','trapmf',[(0.0008-0.0005)/2+0.0005+0.00005*k*(1+0.035) 0.001*k*(1+0.035) 0.0055 0.0055]);
plotmf(a,'input',1);
k2 = 1+0.15;
k3 = 1+0.05;
a = addvar(a,'input','L2',[0 0.012]);
a = addmf(a,'input',2,'small','trapmf',[0 0 0.00015*k2 0.00025*k]);
a = addmf(a,'input',2,'middle','trimf',[0.00015*k3 0.000575*k3 0.001*k3]);
a = addmf(a,'input',2,'big','trapmf',[0.0008*k2 0.001*k2 0.012 0.012]);
figure;
plotmf(a,'input',2);
k4 = 1+0.1;
k5 = 1+0.2;
a = addvar(a,'input','t1',[0 90]);
a= ddmf(a,'input',3,'small','trapmf',[0 0 3*k4*(1+0.05) 6.5*k4*(1+0.05)]);
a=addmf(a,'input',3,'big','trapmf',[3*k5*(1+0.05) 6.5*k5*(1+0.05) 90 90]);
figure;
plotmf(a,'input',3);
k5 = 1+0.05;
k6 = 1+0.1;
a = addvar(a,'input','t2',[0 90]);
a=addmf(a,'input',4,'small','trapmf',[0 0 30*k5*(1+0.05) 32*k5*(1+0.05)]);
a=addmf(a,'input',4,'big','trapmf',[30*k6*(1+0.05) 32*k6*(1+0.05) 90 90]);
figure;
plotmf(a,'input',4);
k7 = 1-0.005;
a = addvar(a,'input','location',[0 260]);
a = addmf(a,'input',5,'left','trapmf',[0 0 80 85]);%it was 70 80
a = addmf(a,'input',5,'right','trapmf',[80 85 260 260]);
figure;
plotmf(a,'input',5);
a = addvar(a,'output','decision',[0 1]);
a = addmf(a,'output',1,'No','trapmf',[0 0 0.4 0.6]);
a = addmf(a,'output',1,'Yes','trapmf',[0.4 0.6 1 1]);
figure;
plotmf(a,'output',1);
ruleList = [ 1 1 1 1 1 1 0.9 1; ...
1 1 1 2 1 1 0.9 1; ...
1 1 2 1 1 1 0.9 1; ...
1 1 2 2 1 1 0.9 1; ...
1 1 1 1 2 1 0.9 1; ...
1 1 1 2 2 1 0.9 1; ...
1 1 2 1 2 1 0.9 1; ...
1 1 2 2 2 1 0.9 1; ...
1 2 1 1 1 1 0.9 1; ...
1 2 1 2 1 1 0.9 1; ...
1 2 2 1 1 1 0.9 1; ...
1 2 2 2 1 1 0.9 1; ...
1 2 1 1 2 1 0.9 1; ...
1 2 1 2 2 1 0.9 1; ...
1 2 2 1 2 1 0.9 1; ...
1 2 2 2 2 1 0.9 1; ...
1 3 1 1 1 1 0.9 1; ...
1 3 1 2 1 1 0.9 1; ...
1 3 2 1 1 1 1 1; ...
1 3 2 2 1 1 0.9 1; ...
1 3 1 1 2 1 0.9 1; ...
1 3 1 2 2 1 0.9 1; ...
1 3 2 1 2 1 1 1; ...
1 3 2 2 2 2 0.9 1; ...
2 1 1 1 1 1 0.9 1; ...
2 1 1 2 1 1 0.9 1; ...
2 1 2 1 1 1 0.6 1; ...
2 1 2 2 1 1 0.9 1; ...
2 1 1 1 2 1 0.9 1; ...
2 1 1 2 2 1 0.9 1; ...
2 1 2 1 2 1 0.6 1; ...
2 1 2 2 2 1 0.9 1; ...
2 2 1 1 1 1 0.9 1; ...
2 2 1 2 1 1 0.9 1; ...
2 2 2 1 1 1 1 1; ...
2 2 2 2 1 1 1 1; ...
2 2 1 1 2 1 0.9 1; ...
2 2 1 2 2 1 0.9 1; ...
2 2 2 1 2 1 1 1; ...
2 2 2 2 2 1 1 1; ...
2 3 1 1 1 1 0.7 1; ...
2 3 1 2 1 1 1 1; ...
2 3 2 1 1 1 1 1; ...
2 3 2 2 1 1 1 1; ...
2 3 1 1 2 1 0.7 1; ...
2 3 1 2 2 1 1 1; ...
2 3 2 1 2 2 1 1; ...
2 3 2 2 2 2 1 1; ...
3 1 1 1 1 1 0.9 1; ...
3 1 1 2 1 1 0.9 1; ...
3 1 2 1 1 1 0.6 1; ...
3 1 2 2 1 1 0.9 1; ...
3 1 1 1 2 1 0.9 1; ...
3 1 1 2 2 1 0.9 1; ...
3 1 2 1 2 2 0.2 1; ...
3 1 2 2 2 1 0.9 1; ...
3 2 1 1 1 1 1 1; ...
3 2 1 2 1 1 1 1; ...
3 2 2 1 1 1 0.5 1; ...
3 2 2 2 1 1 1 1; ...
3 2 1 1 2 1 1 1; ...
3 2 1 2 2 1 1 1; ...
3 2 2 1 2 1 0.5 1; ...
3 2 2 2 2 1 1 1; ...
3 3 1 1 1 1 0.7 1; ...
3 3 1 2 1 1 1 1; ...
3 3 2 1 1 1 1 1; ...
3 3 2 2 1 1 1 1; ...
3 3 1 1 2 1 0.7 1; ...
3 3 1 2 2 1 1 1; ...
3 3 2 1 2 1 1 1; ...
3 3 2 2 2 2 1 1; ...
4 1 1 1 1 1 0.9 1; ...
4 1 1 2 1 1 0.9 1; ...
4 1 2 1 1 1 1 1; ...
4 1 2 2 1 1 0.9 1; ...
4 1 1 1 2 1 0.9 1; ...
4 1 1 2 2 1 0.9 1; ...
4 1 2 1 2 1 1 1; ...
4 1 2 2 2 1 0.9 1; ...
4 2 1 1 1 1 0.9 1; ...
4 2 1 2 1 1 1 1; ...
4 2 2 1 1 1 1 1; ...
4 2 2 2 1 1 1 1; ...
4 2 1 1 2 1 0.9 1; ...
4 2 1 2 2 1 1 1; ...
4 2 2 1 2 2 1 1; ...
4 2 2 2 2 2 1 1; ...
4 3 1 1 1 1 0.9 1; ...
4 3 1 2 1 1 1 1; ...
4 3 2 1 1 2 1 1; ...
4 3 2 2 1 1 1 1;
4 3 1 1 2 1 0.9 1; ...
4 3 1 2 2 1 1 1; ...
4 3 2 1 2 2 1 1; ...
4 3 2 2 2 2 1 1];
a = addrule(a,ruleList);
a = setfis(a,'DefuzzMethod','mom');
fuzzy(a)
showfis(a); %анотация к системе
writefis(a,'fis_lab_fz'); %запись системы на диск