Это интерполяционный полином относительно , принимающий в точках значения .

.

При

.

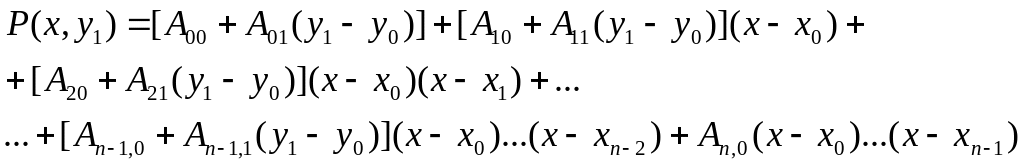
–разделенная разность по

.

Аналогично, для всех :

.

Обобщенный интерполяционный полином Ньютона для неравных

промежутков в случае интерполирования функции двух переменных

(3.30)

Аппроксимация функций, заданных таблицей, по методу наименьших квадратов

– система линейно независимых функций на , .

Строим так, чтобы было минимальным.

(3.31)

Если – неодинаковой точности, вводим веса

. (3.32)

Теория построения обобщенных основана на теории, изученной в предыдущих пунктах.

и на .

и – тождественны, если .

Скалярное произведение функций и :

, (3.33)

где > – заданные числа, в частности все .

Норма:

. (3.34)

Все свойства скалярного произведения и нормы выполняются.

Функции образуют систему функций Чебышева.



Обобщенный полином , принимающий в точках заданные значения, единственен.

 обобщенный интерполяционный многочлен.

 приближение по методу наименьших квадратов.

Примеры аппроксимации

Пример 1.

Функцию



, – наименьшее значение.

.

.

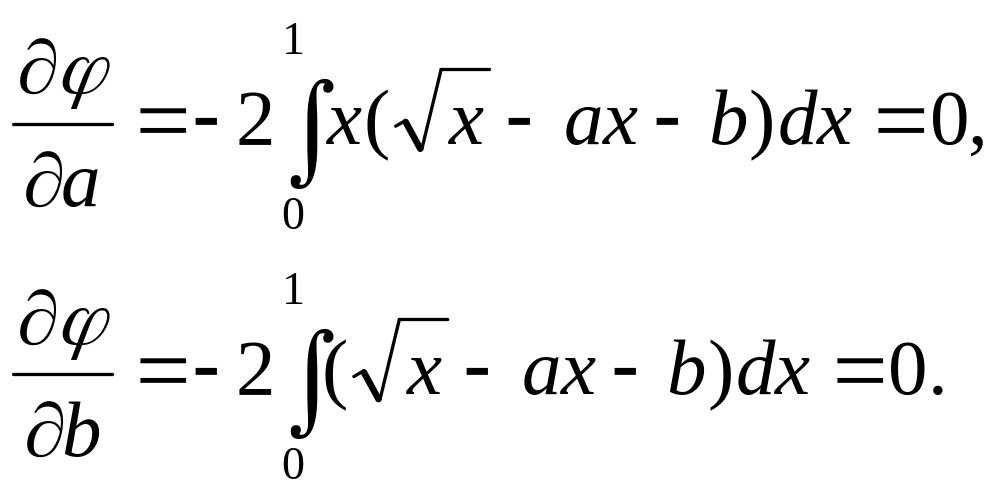
– наилучшее приближение для

погрешность .

Пример 2.

– многочлен, у него нет корней на и при .

Вычислить .

,

Погрешность – 0.2% .

Пример 3.

– некоторая функция.

 , погрешность min

.

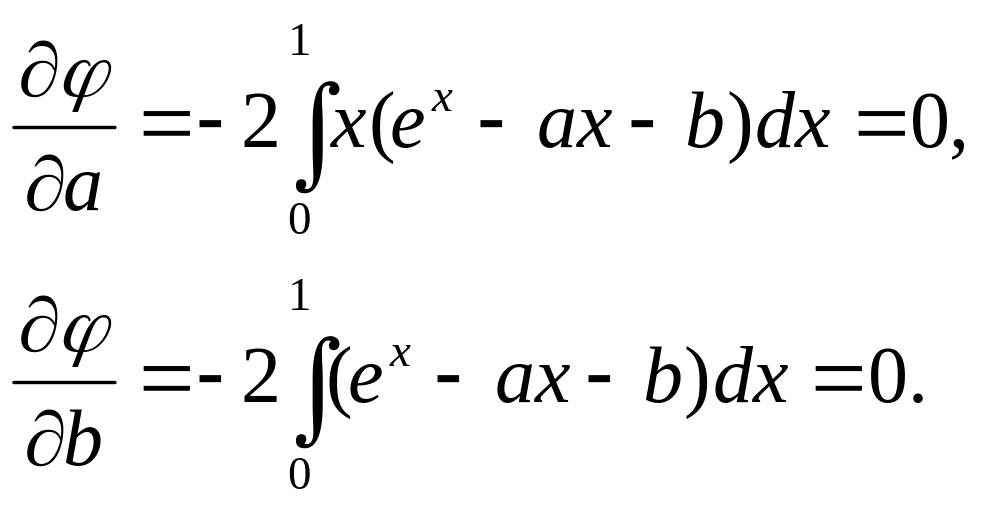
Погрешность:

,

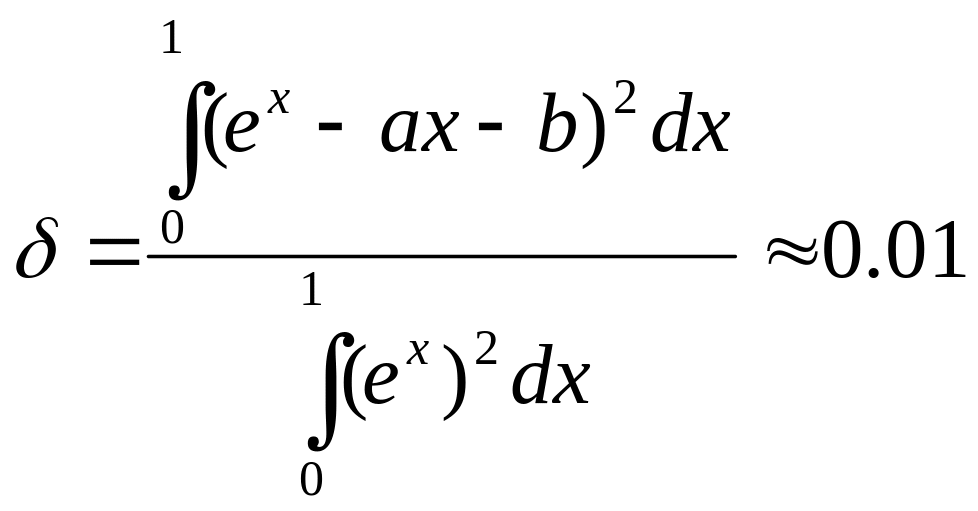, т.к.

Пример 4. Неудачный выбора базиса.

Базис –{1, x}.

Пусть .

Базис подпространства – функции . .

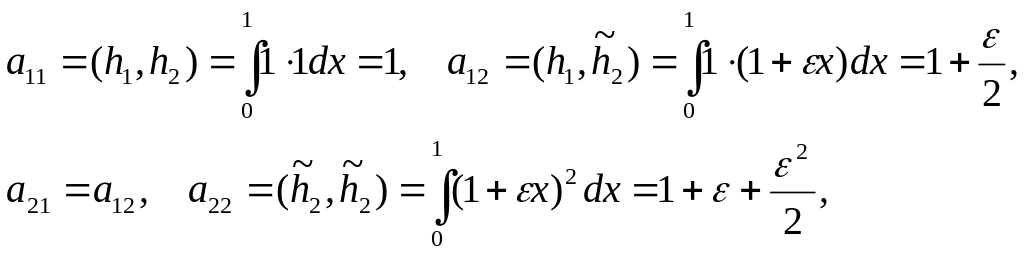
Определитель Грамма .

Пусть , тогда .