21

Тема №3

Многочлены Чебышева.

Оптимизация погрешности интерполяции.

Сходимость интерполяционного процесса.

Сплайн-интерполирование.

Построение кубического сплайна.

Интерполирование с кратными узлами. Многомерная интерполяция.

Аппроксимация функций, заданных таблицей, по методу наименьших квадратов

Многочлены Чебышева

Первая последовательность, , многочлен Чебышёва первого рода характеризуется как многочлен степени n>1 со старшим коэффициентом 2^n-1, который меньше всего отклоняется от нуля на интервале [-1,1].

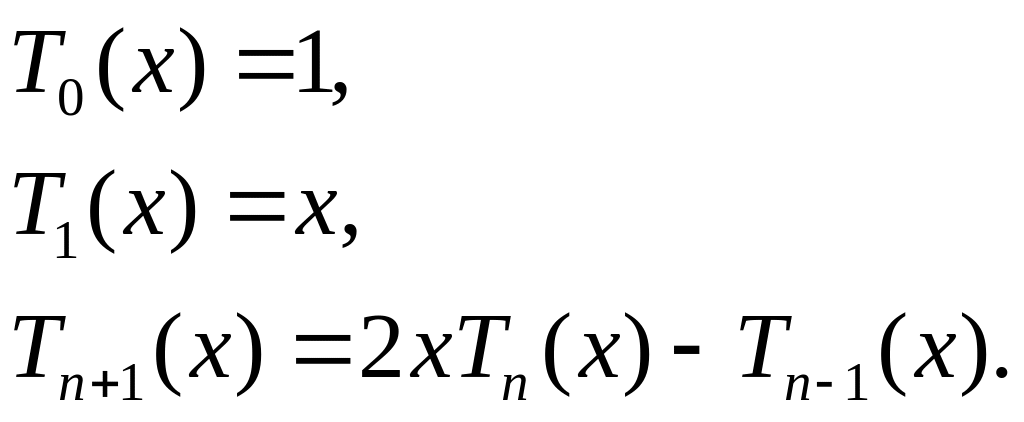
Вторая последовательность, , многочлен Чебышёва второго рода характеризуется как многочлен степени n со старшим коэффициентом 2ⁿ, интеграл абсолютного значения которого по интервалу [-1,1] наименьший возможный.

Тригонометрическое определение многочлена Чебышёва:

Многочлены Чебышёва первого рода :

.

Многочлены Чебышёва второго рода :

Примеры

Несколько первых многочленов Чебышёва первого рода:

Несколько первых многочленов Чебышёва второго рода:

Многочлены Чебышева первого рода

Определение 1. Многочлен Чебышева – функция

, (3.1)

где .

– многочлен при любом . Так как

и

,





Корни полинома Чебышева



Корни: – n корней на отрезке [-1,1].

Точки экстремума на [-1,1]

Из (3.2):

 точки экстремума:

Причем

Многочлены, наименее уклоняющиеся от нуля

.

Лемма. Если – произвольный многочлен степени n со старшим коэффициентом единица, то

. (3.3)

Доказательство от противного

Разность – многочлен степени (n -1).

В точках экстремумов полинома Чебышева , т.к. согласно предположению при любом m.



Между каждыми двумя точками многочлен меняет знак



Многочлен степени (n-1) имеет n различных корней



Противоречие

Многочлен таков, что его максимальное по модулю значение на отрезке [-1,1] не превосходит максимального по модулю значения на том же отрезке любого другого многочлена степени n со старшим коэффициентом единица

Определение 2. Многочлен называется многочленом, наименее уклоняющимся от нуля на отрезке [-1,1].

Более сильное утверждение:

Замена  отрезок [-1,1] переводится в отрезок .

, (3.4)

Старший коэффициент – единица;

– многочлен, наименее уклоняющийся от нуля на отрезке .

Корни многочлена (3.4) :

. (3.5)

Е

сли – любой многочлен степени n со старшим коэффициентом единица, то

Минимизация оценки остаточного члена интерполяционного многочлена Лагранжа (выбор узлов интерполирования)

Приближение на с узлами интерполяции – интерполяционным полиномом Лагранжа.

Оценка погрешности интерполяционного полинома Лагранжа:

Здесь – обозначение равномерной нормы , –точная верхняя граница .

Оценка:

(3.6)

где .

Как минимизировать выражение, стоящее справа в оценке (3.6)?

– многочлен степени (n+1) со старшим коэффициентом единица.

при произвольном выборе узлов интерполяции.

Если узлы интерполирования – корни полинома Чебышева : ,

.

Оценка погрешности интерполяционного полинома Лагранжа:

.



Если в качестве узлов интерполяции взяты корни полинома Чебышева, то получаем наименьшую погрешность интерполяции на отрезке при фиксированном числе узлов интерполяции.

О сходимости интерполяционного процесса

Можно ли повысить точность интерполяции на отрезке?

Последовательность узлов интерполяции:

, (3.8)

Интерполяционный процесс для функции :

  последовательность

Определение 3 Определение поточечной сходимости: интерполяционный процесс для функции сходится в точке , если существует .

Определение 4. Определение равномерной сходимости: интерполяционный процесс сходится равномерно на , если при .

Фабер: для любой системы узлов вида (3.8) найдется такая непрерывная функция , что построенные для нее интерполяционные многочлены Лагранжа по этим узлам не сходятся равномерно на к .

Бернштейн: последовательность интерполяционных полиномов Лагранжа , построенных для функции на отрезке по равноотстоящим узлам ( не стремится с возрастанием n к ни в одной точке отрезка за исключением точек -1, 0, 1.

Марцинкевич: если непрерывна на , то найдется такая последовательность сеток, для которой соответствующий интерполяционный процесс сходится равномерно на . Однако строить такие сетки очень сложно, причем для каждой нужно строить свою последовательность сеток.



В общем случае нет равномерной сходимости интерполяционного процесса, не имеет смысла строить интерполяционные многочлены высокой степени, т.к. при этом накапливается вычислительная погрешность

Сплайн–интерполяция

Отрезок с точками сетки разбит на систему подотрезков: . – значения функции в узлах сетки.

Определение 5. Интерполяционным сплайном степени m для функции , построенным по системе подотрезков на отрезке , называется функция , которая удовлетворяет следующим условиям:

1) на каждом подотрезке она является многочленом степени m ;

2) на всем отрезке она (m-1) раз непрерывно дифференцируема;

3) в узлах сетки она принимает заданные значения: .

Пример. Построение кубического сплайна .

Для подотрезка :

(3.9)

где – коэффициенты, подлежащие определению.

Условия определения коэффициентов:

1. непрерывность функции , её первой и второй производных в узлах системы подотрезков ;

2. требований .

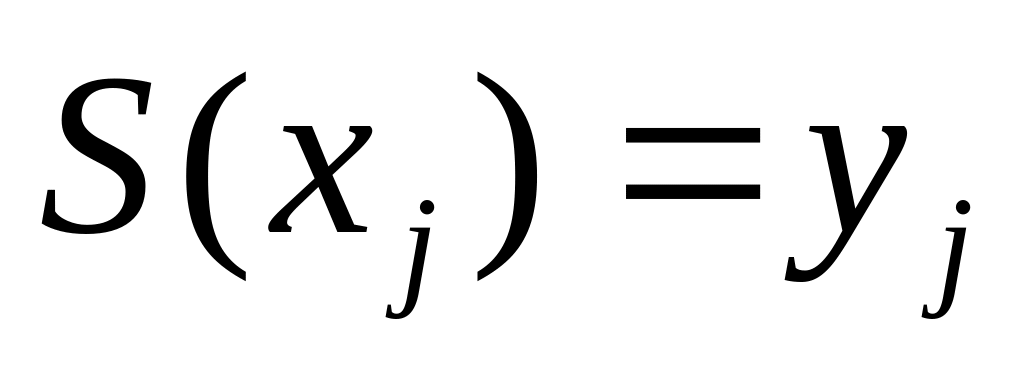1. Удовлетворение требованиям интерполяции и непрерывности в узлах сетки:

при и :

, (3.10)

. (3.11)

2. Удовлетворение требованиям непрерывности и :

(3.12)

. (3.13)

Получили уравнения на неизвестных коэффициентов .

3. Краевые условия на концах отрезка зависят от решаемой задачи: например, и :

. (3.14)



Система линейных алгебраических уравнений относительно неизвестных. Решим ее следующим образом.

Из (3.10) находим все . Из (3.13) и (3.14) выражаем через :

. (3.15)

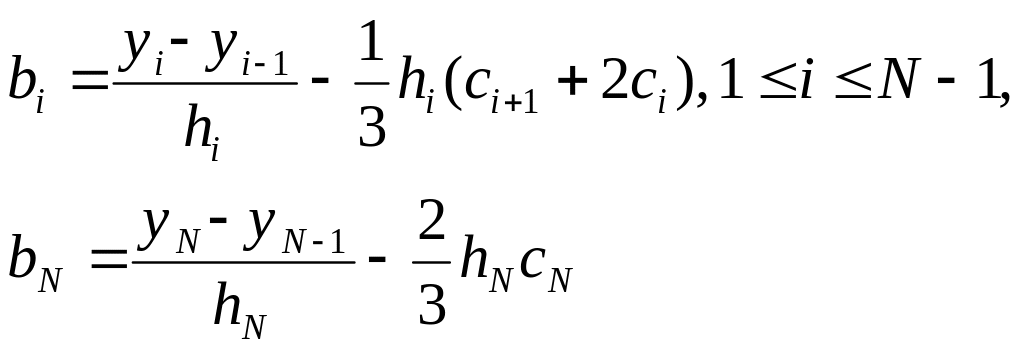(3.16)

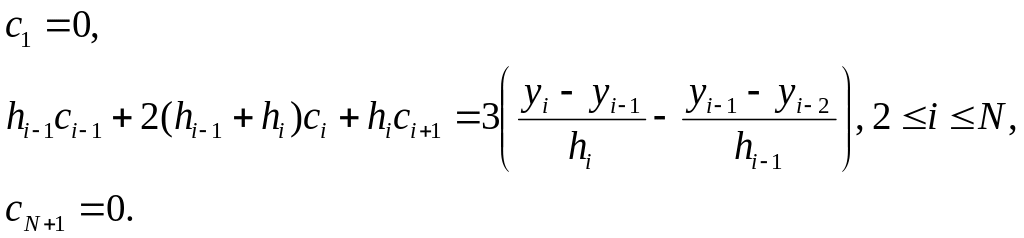(3.17)

Теорема 1. Пусть . Тогда для интерполяционного кубического сплайна , построенного на сетке , справедливы неравенства

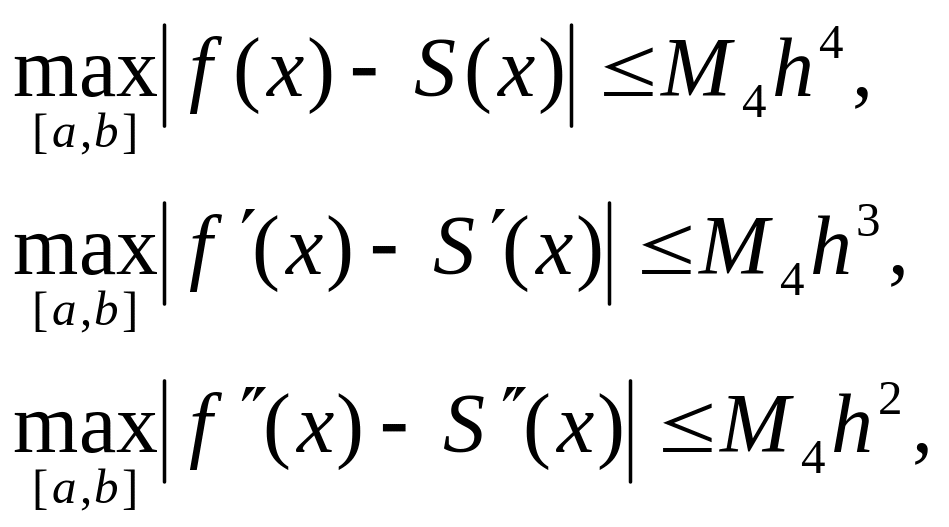
где

.