8. Операционный метод математического описания линейных систем. Типовые звенья: позиционные, дифференцирующие, интегрирующие и их характеристики.

Операционный метод решения уравнений динамики систем предусматривает следующее: вначале исходное уравнение приводят к операторной форме, применяя преобразование Лапласа, с учетом заданных начальных условий; затем разрешают полученное алгебраическое уравнение относительно искомой величины, записанной в операторной форме, используя в случае необходимости свойства преобразования Лапласа; и наконец, применяя операцию обратного преобразования Лапласа, находят решение исходного уравнения динамики в обычной форме.

Прямым преобразованием Лапласа функции f(t) действительного переменного t называется функция F(p) комплексного аргумента р=α+iw, определяемая формулой

где L — символ операции прямого преобразования Лапласа.

Функция f(t) может быть преобразована по Лапласу, если при t<0 она равна нулю, а при t>0 — кусочно-непрерывна и возрастает не быстрее некоторой показательной функции M exp(p₀t), где М и р₀ — постоянные: причем М>0, а р₀≥0. Последнее условие обеспечивает сходимость интеграла Лапласа (I,21). Обычно переходные процессы, протекающие в системах регулирования и являющиеся функцией времени, удовлетворяют этим трем условиям.

Функцию f(t), подвергаемую преобразованию Лапласа, называют оригиналом, а функцию F(р), вычисленную по уравнению (I,21),— изображением. Оригиналы обозначают строчными буквами, а изображения — прописными.

Уравнение динамики системы в операторной форме всегда проще исходного дифференциального уравнения. При этом оно учитывает начальные условия и отражает физическую картину переходного процесса в системе.

Для отыскания оригинала по соответствующему изображению F(p) необходимо провести операцию обратного преобразования Лапласа, которая обозначается символом L^-1:

Вычисление этого интеграла сопряжено с большими трудностями. Поэтому если изображение F(p) имеется в таблице или может быть приведено к табличному виду, то оригинал находят по таблице. В противном случае изображение F(p) необходимо предварительно привести к форме, удобной для последующего нахождения оригинала.

Структурные схемы систем и их типовые динамические звенья.

Для исследования различных по природе и конструкции систем регулирования с помощью единого математического аппарата их представляют в виде структурных схем. Такие схемы содержат узлы разветвления, узлы суммирования и динамические звенья (рис. I-10).

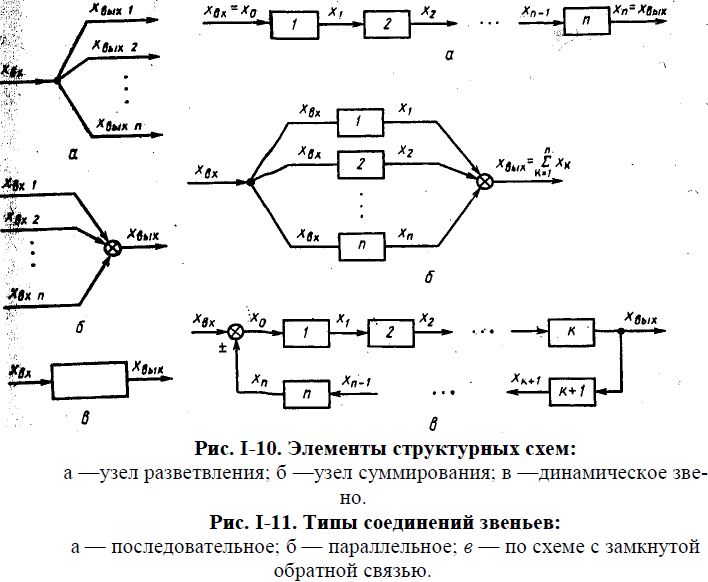
Узел разветвления. В таком узле входной сигнал х_вх разделяется, не меняя своего значения, и направляется далее по нескольким каналам

где x_вых1, x_вых2, …, x_{вых n} — сигналы в выходных каналах узла разветвления.

Суммирующий узел, к которому подходит несколько сигналов x_вх1, x_вх2, …, x_{вх n} формирует на выходе только один сигнал x_вых, равный алгебраической сумме входных сигналов

Динамическое звено. Проходя такое звено, входной сигнал x_вх изменяет сигнал на выходе x_вых по форме и величине (в некоторых случаях только по величине).

В основу классификации звеньев положены соответствующие уравнения динамики. Переходные процессы систем регулирования (пневматических, электрических, механических и др.), имеющих разную физическую природу и различное конструктивное оформление, но обладающих одинаковыми динамическими свойствами, подобны. Поэтому каждая такая система описывается одним или несколькими одинаковыми звеньями.

Большинство звеньев обладает направленностью действия (детектирующее свойство). Сигнал проходит через них только в одном направлении — с входа звена на его выход, в обратном направлении звено сигнал не пропускает. Например, изменение температуры рабочего спая термоэлектрического преобразователя приводит к изменению термоэлектродвижущей силы на его свободных концах.

Звенья систем могут быть статическими и астатическими. У статического звена при постоянном входном воздействии выходная величина со временем устанавливается на постоянном значении, отличном от первоначального, а у астатического звена в установившемся режиме выходная величина непрерывно изменяется с постоянной скоростью или ускорением.

Динамические звенья называют типовыми, если изменение проходящего через них сигнала описывается алгебраическим или дифференциальным уравнением не выше 2-го порядка. Они имеют одну входную и одну выходную величину. Титовыми звеньями являются: усилительное, интегрирующее, дифференцирующее, апериодическое, колебательное и запаздывающее. В табл. I.3 приведены уравнения динамики указанных звеньев, их переходные характеристики и графики.

Соединения звеньев. В реальных системах звенья объединяют последовательно, параллельно, а также в соединения с замкнутой обратной связью (рис I-11). При последовательном соединении звеньев (рис. I-11, а) выходная величина предыдущего звена без искажения поступает на вход последующего звена. При таком соединении звеньев входной величиной является входная величина первого по ходу сигнала звена, а выходной— выходная величина последнего из них.

При параллельном соединении звеньев (рис I-11; б) входной сигнал через узел разветвления поступает на входы всех элементарных звеньев. Выходные сигналы этих звеньев суммируются и направляются на выход соединения.

При замкнутой обратной связи (рис. I-11, в) система состоит из двух цепочек звеньев, каждая из которых может представлять собой достаточно сложное соединение. По одной из этих цепочек сигнал проходит последовательно через звенья от входа соединения к его выходу, т.е. по прямой связи, а по другой — от выхода соединения к входу, т.е. по обратной связи. При этом на вход первой цепочки звеньев подается сигнал x₀, равный сумме входной величины соединения х_вх и выходной величины второй цепочки звеньев х_п

Выходной величиной такого соединения х_вых является выход к-го звена; одновременно этот же сигнал подается на вход (к + 1)-го звена.

Если сигнал с выхода обратной связи и основной входной сигнал соединения действуют в одном направлении, то обратная связь называется положительной, а если эти сигналы действуют в противоположных направлениях — отрицательной.

Комбинации этих соединений звеньев позволяют представить любую сложную АСР химико-технологического процесса.

Выше рассматривались звенья и соединения только с одной входной и одной выходной величинами. Однако большое число реальных химико-технологических объектов, а также систем регулирования обычно представляют собой соединения звеньев, имеющих несколько входных и выходных величин. Такие соединения имеют несколько каналов прохождения сигналов.