5. Частотные характеристики систем. Частота среза. Вычисление частотной передаточной функции.
Частотные характеристики систем.
Частотные характеристики определяют динамические свойства АСР и широко используются в инженерной практике для их расчета.
Если на вход системы подать гармонические колебания хвх (частота wi, амплитуда Aвх), которые в комплексной форме имеют вид
(здесь eiw1t = cosw1t+isinw1t) то на выходе этой системы через достаточно большой промежуток времени установятся вынужденные колебания хвых с той же частотой w1, но с другой амплитудой Авых1 и со сдвигом по фазе φ1 (рис. I-12)
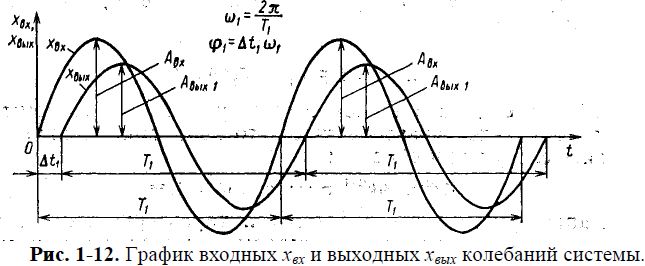
Отношение выходных колебаний системы хвых к входным хвх, выраженное в комплексном виде, называют комплексным коэффициентом передачи системы при частоте w1
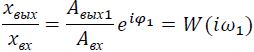
С изменением частоты колебаний на входе (при постоянной амплитуде Авх) амплитуда выходных колебаний Авых и фазовый сдвиг φ будут меняться, что вызовет изменение комплексного коэффициента передачи системы.
Совокупность всех значений комплексного коэффициента передачи при изменении φ от 0 до +∞ называют комплексной частотной характеристикой системы или амплитудно-фазовой характеристикой (АФХ) системы и обозначают через W(iw).
Зависимость отношения амплитуд выходных и входных колебаний Авых/Авх от частоты колебаний w называют амплитудно-частотной характеристикой (АЧХ) и обозначают через А(w). Зависимость фазового сдвига выходных колебаний относительно входных φ от частоты колебаний w называют фазо-частотной характеристикой (ФЧХ) и обозначают через φ(w). Эти частотные характеристики связаны между собой уравнением
Графически АФХ представляет собой кривую, описываемую на комплексной плоскости концом вектора, модуль которого равен значениями A(w), а аргумент — φ(w) при изменении w от 0 до +∞.
Проекцию АФХ на действительную ось комплексной плоскости называют вещественной частотной характеристикой (ВЧХ) и обозначают через U(w), а проекцию на мнимую ось — мнимой частотной характеристикой (МЧХ) и обозначают через V(w).
Частотные характеристики могут быть определены одна через другую с помощью следующих зависимостей:
Частотные характеристики выражают зависимость параметров установившихся выходных колебаний от параметров входных колебаний при одинаковых частотах. Они отображают квазиустановившиеся процессы в системе и в полной мере определяют ее динамические свойства. Частотные характеристики системы или звена можно определить по их уравнениям динамики.
Сравнивая полученное выражение с выражением передаточной функции этого звена (1,39), отметим, что они совпадают за исключением множителей р и iw. Этот вывод справедлив для всех звеньев и систем.
Следовательно, аналитическое выражение АФХ системы n-го порядка, уравнение движения которой описывается равенством (I,6) а передаточная функция — зависимостью (1,38), может быть получено путем замены комплексной величины р в уравнении (1,38) на мнимую величину iw
Аналитические выражения остальных частотных характеристик звена или системы находят по выражению АФХ. Для этого сначала освобождаются от мнимости в знаменателе АФХ и разделяют полученную комплексную величину на вещественную и мнимую части, т. е. находят соответственно ВЧХ и МЧХ. Затем по равенствам (I,58) и (I,59) определяют АЧХ и ФЧХ.
Частотные характеристики типовых динамических звеньев приведены также в табл. 1.4.
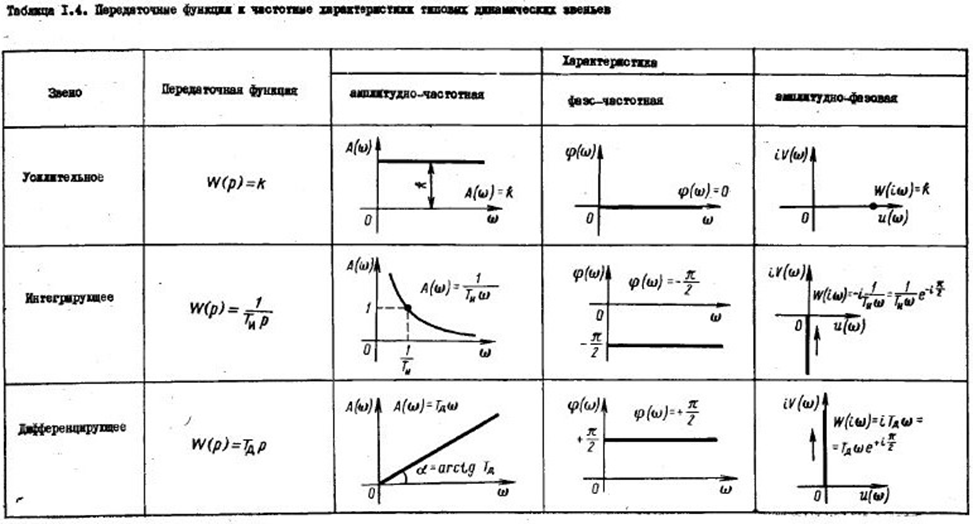
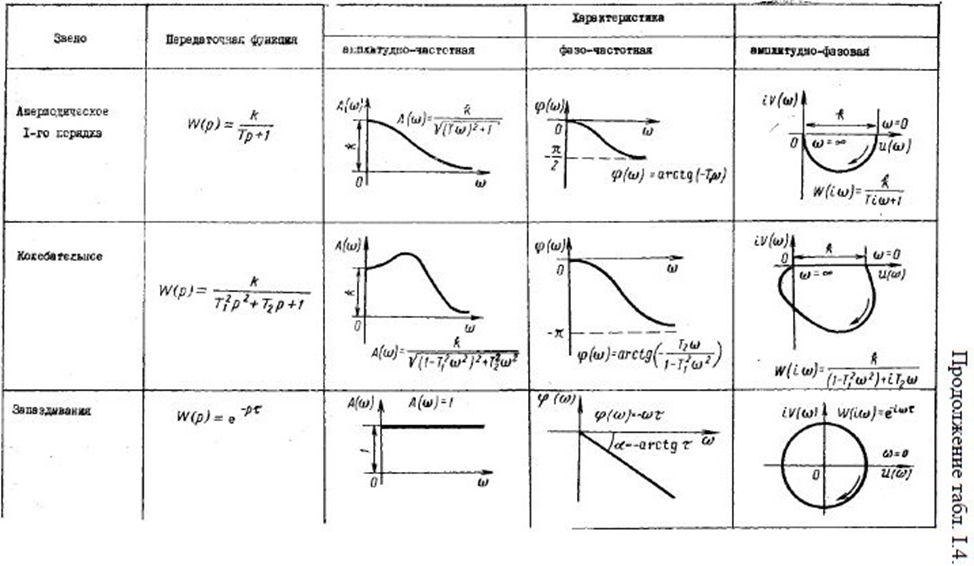
Если известны структурная схема системы и уравнения динамики всех ее звеньев, то для определения АФХ системы обычно находят аналитические выражения передаточных функций всех звеньев системы и по ним, используя зависимости (I,41), (I,44), (I,48) и (I,49) и правила преобразования структурных схем, определяют передаточную функцию системы. Заменяя в полученном выражении комплексную переменную р на ею, находят АФХ системы.
Логарифмические частотные характеристики. Такие характеристики также находят применение в расчетах АСР. Зависимость lg A(w), построенную в логарифмическом масштабе частот по оси абсцисс, называют логарифмической амплитудно-частотной характеристикой (ЛАЧХ). При этом по оси ординат обычно откладывают не величину lg A(w), а пропорциональную ей величину L(w), выраженную в децибелах. Соответствие между A(w) в натуральных единицах и L(w) в децибелах определяется равенством
Зависимость φ(w), построенную в логарифмическом масштабе частот по оси абсцисс, называют логарифмической фазо-частотной характеристикой (ЛФЧХ). Фазовый угол по оси ординат откладывают в градусах или радианах.
При построении логарифмических характеристик частоты откладывают в декадах. Декадой называют интервал изменения частоты в 10 раз.
Логарифмические частотные характеристики на больших участках изменения w без большой погрешности можно заменить прямыми. Всю же характеристику можно аппроксимировать ломаной кривой, состояли из нескольких прямолинейных отрезков (асимптот). Асимптотическую ЛАЧХ обозначают через Lа(w), а асимптотическую ЛФЧХ — через φа(w). Для построения асимптотических логарифмических характеристик достаточно определить наклоны прямолинейных отрезков и координаты точек их сопряжения. Аппроксимация логарифмических частотных характеристик прямыми значительно облегчает их построение и поэтому именно они обычно используются в инженерной практике для расчета систем.
Асимптотические логарифмические частотные характеристики системы находятся довольно просто при последовательном соединении входящих в нее звеньев. Для этого на одно поле чертежа наносят характеристики отдельных звеньев, а затем в соответствии с равенствами
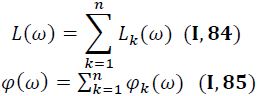
определяют значения их ординат при сопрягающих частотах и соединяют полученные точки отрезками прямых.
По временным характеристикам, передаточным функциям, характеристическим уравнениям или частотным характеристикам можно определить динамические свойства технологических объектов, регуляторов и других элементов, а также АСР.
Нахождение передаточных функций системы. Передаточные функции систем могут быть найдены по уравнениям динамики и по передаточным функциям звеньев системы.
По уравнению динамики передаточные функции находятся следующим образом. При нахождении, в частности, по уравнению (I,6) сначала запишем его в изображениях:
или обозначая полиномы в левой и правой частях уравнения через D(p) и К(р), получим
где U (р) — полином, определяемый начальными условиями системы. Полагая в уравнениях (I,36) и (I,37) начальные условия нулевыми [при этом U(p)=0], из равенств (I, 34), (I, 36) и (I,37) получим выражение для передаточной функции системы:
Таким образом, передаточная функция систем, движение которых описывается уравнениями типа (I,6), является дробно-рациональной функцией независимого переменного р. В реальных системах автоматики степень полинома знаменателя в выражении (1,38) всегда выше или равна степени полинома числителя, т. е. п≥т. Корни полинома числителя передаточной функции называют нулями, а корни полинома знаменателя — полюсами. При р = 0 передаточная функция системы вырождается в обычный коэффициент усиления системы.
Отметим, что передаточная функция системы может быть также определена, как отношение полиномов правой и левой частей уравнения (I,9).
Аналогичный результат можно получить, если записать уравнение (I,27) в виде (I,9), а затем взять отношение полиномов правой и левой частей уравнения.
Передаточные функции типовых звеньев приведены в табл. 4.
По передаточным функциям звеньев также могут быть найдены передаточные функции систем. Для нахождения передаточной функции системы W(p), состоящей из п последовательно соединенных звеньев, передаточные функции которых соответственно обозначены через W1(p), W2(р),…, Wn(р) (см. рис. I-11, а), напишем для каждого ее звена уравнение, подобное уравнению (I,35)
Исключим из системы (I,40) промежуточные величины
Сравнивая полученное с уравнением (I,35), найдем
Таким образом, при последовательном соединении звеньев передаточная функция системы равна произведению передаточных функций входящих в нее звеньев.
Для нахождения передаточной функции системы W(p), составленной из п параллельно соединенных звеньев, передаточные функции которых соответственно равны W1(p), W2(p),…, Wn(p) (см. рис. I-11,б), определим Лапласовы изображения выходных величин всех звеньев системы:
Запишем в изображениях уравнение (I,32) для суммирующего звена
Подставляя выражения для х1(p), х2(р) и т. д. в полученное уравнение, имеем
Сравнивая уравнения (I,35) и (I,43), окончательно получим
Таким образом, при параллельном соединении звеньев передаточная функция системы равна сумме передаточных функций входящих в нее звеньев.
Для нахождения передаточной функции соединения с замкнутой обратной связью (структурную схему см. на рис. 1-11, в) относительно величины xвых введем следующие обозначения: W1(p)—передаточная функция цепочки звеньев прямой связи; W2 (р) — передаточная функция цепочки звеньев обратной связи. Тогда передаточные функции W1(p) и W2 (р) можно выразить
При положительной обратной связи, когда сигналы прямой и обратной связей складываются, для суммирующего узла
Из уравнений (I,45) и (I,46) найдем соответственно величины Хо(р) и Хп(р)
Подставляя полученные выражения в уравнение (I,47), имеем
Сгруппируем в левой части члены, содержащие хвых(р)
Из последнего равенства найдем отношение хвых(р)/хвх(р) которое и является искомой передаточной функцией
Таким образом, передаточная функция соединения с замкнутой положительной обратной связью представляет собой дробь, числитель которой равен передаточной функции цепочки звеньев прямой связи, а знаменатель — выражению: единица минус произведение передаточных функций цепочек прямой и обратной связей (или единица минус передаточная функция соединения в разомкнутом состоянии).
Для нахождения передаточной функции соединения с замкнутой отрицательной обратной связью, в котором сигналы прямой и замыкающей обратной связей вычитаются, можно воспользоваться уравнением (I,48) при условии изменения знака минус в знаменателе на плюс
Однако, следует иметь в виду, что при расчете систем указанные знаки в знаменателе передаточных функций соединений (I,48) и (I,49) должны определяться с учетом знаков передаточных функций звеньев, входящих в эти соединения.
Аналогичным образом может быть найдено выражение для передаточной функции соединения с замкнутой обратной связью относительно любой промежуточной величины.