4. Уравнение динамики линейной системы n-го порядка. Передаточные функции. Временные характеристики систем.

Уравнение динамики линейной системы n-го порядка с одной входной и одной выходной величинами это неоднородное линейное дифференциальное уравнение с постоянными коэффициентами:

где а₀, а₁,…, а_п-1, а_п; b₀,b₁,…, b_п-1, b_п; — постоянные коэффициенты, зависящие от параметров входящих в систему элементов; i — время.

В физически реализуемых системах порядок левой части этого уравнения выше или равен порядку правой части уравнения, т. е. п ≥ т. В левой части уравнения группируют слагаемые, содержащие выходную величину и ее производные, а в правой — слагаемые с входной величиной и ее производными. При нескольких входных величинах все слагаемые, содержащие входные величины и их производные, записывают в правую часть уравнения. При наличии нескольких выходных величин поведение системы в переходном режиме описывают системой уравнений динамики, число которых равно числу выходных величин.

Решение уравнения динамики (I,6) представляет собой зависимость изменения выходной величины системы во времени при известном входном воздействии. По полученному решению определяют качество переходного процесса.

Уравнение динамики (I,6) при х_вх = 0 имеет вид:

Это однородное уравнение. Оно характеризует поведение системы, предоставленной самой себе, после снятия внешних возмущений. Его называют уравнением свободного движения системы.

Из уравнения динамики (I, 6) можно получить уравнение статики системы, приравняв в нем все производные нулю. Оно имеет вид уравнения (I,5), если k — b_m/a_m.

Обычно, входные и выходные величины в уравнениях статики и динамики записывают в относительном виде. При этом постоянные коэффициенты уравнения динамики или безразмерны, или имеют размерность времени в степени, равной порядку производной соответствующего слагаемого.

Для упрощения записи уравнения динамики операцию дифференцирования обозначают символом р (здесь р — алгебраическая величина):

Аналогично операцию интегрирования обозначают 1/p:

Таким образом

Используя эти соотношения, получим следующую запись уравнения динамики системы (I, 6):

Заменяя полином в левой части уравнения (1,8) через D(p) а в правой части через К(р), окончательно получим

где D(p) —полином, характеризующий свободные колебания системы; К(р) —полином, характеризующий внешнее возмущение.

Передаточные функции систем.

Передаточные функции, как и уравнения динамики, характеризуют изменение сигнала при прохождении через систему.

Отношение Лапласовых изображений выходной и входной величин системы при нулевых начальных условиях называется передаточной функцией системы W(p)

где x_вх(p) и x_вых(p)— изображения по Лапласу входной и выходной величин системы.

По передаточной функции системы W(p) и изображению ее входной величины можно найти изображение выходной величины

При наличии одной входной и одной выходной величины система или звено имеют только один канал прохождения сигнала, а следовательно, и одну передаточную функцию. Если же система или звено имеют несколько каналов прохождения сигнала, что возможно при нескольких входных и выходных величинах, то прохождение сигнала в каждом канале характеризуется своей передаточной функцией.

Нахождение передаточных функций системы. Передаточные функции систем могут быть найдены по уравнениям динамики и по передаточным функциям звеньев системы.

По уравнению динамики передаточные функции находятся следующим образом. При нахождении, в частности, по уравнению (I,6) сначала запишем его в изображениях:

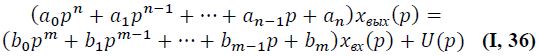
или обозначая полиномы в левой и правой частях уравнения через D(p) и К(р), получим

где U (р) — полином, определяемый начальными условиями системы. Полагая в уравнениях (I,36) и (I,37) начальные условия нулевыми [при этом U(p)=0], из равенств (I, 34), (I, 36) и (I,37) получим выражение для передаточной функции системы:

Таким образом, передаточная функция систем, движение которых описывается уравнениями типа (I,6), является дробно-рациональной функцией независимого переменного р. В реальных системах автоматики степень полинома знаменателя в выражении (1,38) всегда выше или равна степени полинома числителя, т. е. п≥т. Корни полинома числителя передаточной функции называют нулями, а корни полинома знаменателя — полюсами. При р = 0 передаточная функция системы вырождается в обычный коэффициент усиления системы.

Отметим, что передаточная функция системы может быть также определена, как отношение полиномов правой и левой частей уравнения (I,9).

А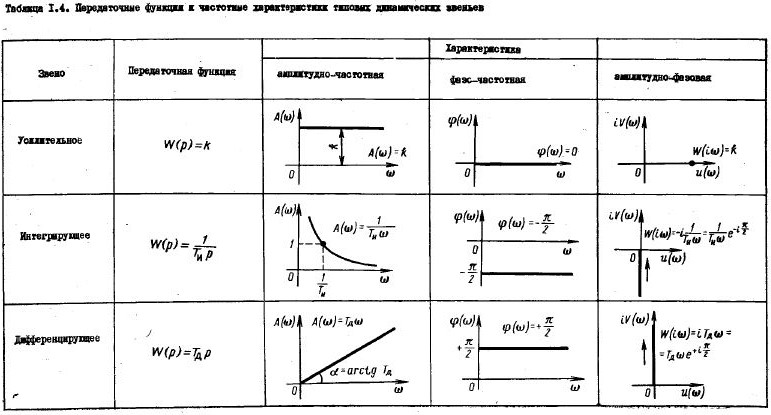 налогичный результат можно получить, если записать уравнение (I,27) в виде (I,9), а затем взять отношение полиномов правой и левой частей уравнения.

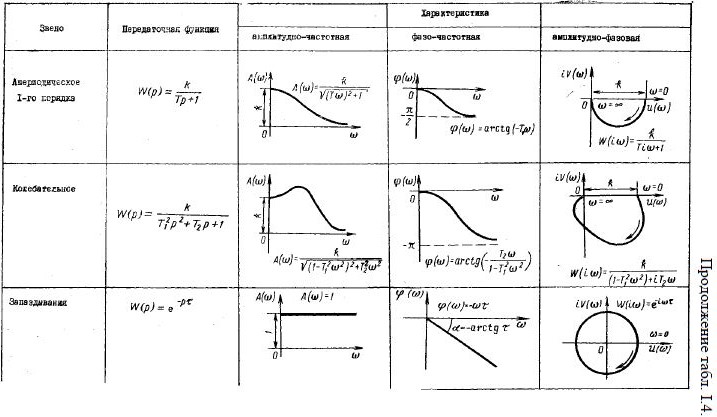
Передаточные функции типовых звеньев приведены в табл. 4.

По передаточным функциям звеньев также могут быть найдены передаточные функции систем. Для нахождения передаточной функции системы W(p), состоящей из п последовательно соединенных звеньев, передаточные функции которых соответственно обозначены через W₁(p), W₂(р),…, W_n(р) (см. рис. I-11, а), напишем для каждого ее звена уравнение, подобное уравнению (I,35)

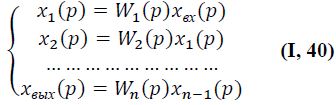
Исключим из системы (I,40) промежуточные величины

Сравнивая полученное с уравнением (I,35), найдем

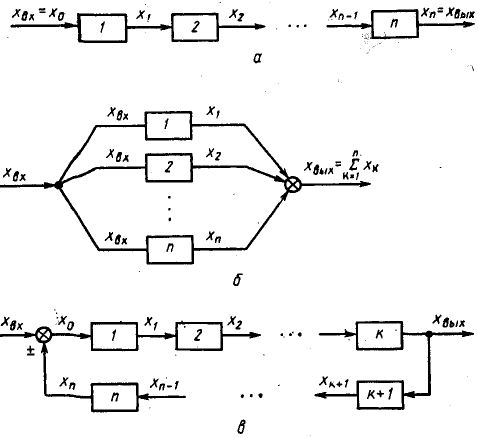
Таким образом, при последовательном соединении звеньев передаточная функция системы равна произведению передаточных функций входящих в нее звеньев.

Для нахождения передаточной функции системы W(p), составленной из п параллельно соединенных звеньев, передаточные функции которых соответственно равны W₁(p), W₂(p),…, W_n(p) (см. рис. I-11,б), определим Лапласовы изображения выходных величин всех звеньев системы:

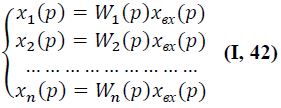
Запишем в изображениях уравнение (I,32) для суммирующего звена

Подставляя выражения для х₁(p), х₂(р) и т. д. в полученное уравнение, имеем

Сравнивая уравнения (I,35) и (I,43), окончательно получим

Таким образом, при параллельном соединении звеньев передаточная функция системы равна сумме передаточных функций входящих в нее звеньев.

Для нахождения передаточной функции соединения с замкнутой обратной связью (структурную схему см. на рис. 1-11, в) относительно величины x_вых введем следующие обозначения: W₁(p)—передаточная функция цепочки звеньев прямой связи; W₂ (р) — передаточная функция цепочки звеньев обратной связи. Тогда передаточные функции W₁(p) и W₂ (р) можно выразить

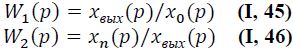
При положительной обратной связи, когда сигналы прямой и обратной связей складываются, для суммирующего узла

Из уравнений (I,45) и (I,46) найдем соответственно величины Х_о(р) и Х_п(р)

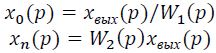
Подставляя полученные выражения в уравнение (I,47), имеем

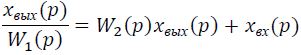
Сгруппируем в левой части члены, содержащие х_вых(р)

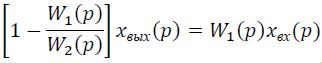
Из последнего равенства найдем отношение х_вых(р)/х_вх(р) которое и является искомой передаточной функцией

Таким образом, передаточная функция соединения с замкнутой положительной обратной связью представляет собой дробь, числитель которой равен передаточной функции цепочки звеньев прямой связи, а знаменатель — выражению: единица минус произведение передаточных функций цепочек прямой и обратной связей (или единица минус передаточная функция соединения в разомкнутом состоянии).

Для нахождения передаточной функции соединения с замкнутой отрицательной обратной связью, в котором сигналы прямой и замыкающей обратной связей вычитаются, можно воспользоваться уравнением (I,48) при условии изменения знака минус в знаменателе на плюс

Однако, следует иметь в виду, что при расчете систем указанные знаки в знаменателе передаточных функций соединений (I,48) и (I,49) должны определяться с учетом знаков передаточных функций звеньев, входящих в эти соединения.

Аналогичным образом может быть найдено выражение для передаточной функции соединения с замкнутой обратной связью относительно любой промежуточной величины.

Временные характеристики систем.

Временная характеристика системы представляет собой изменение выходной величины во времени при подаче на ее вход типового апериодического воздействия. В качестве последнего используют единичное ступенчатое воздействие, или единичный импульс. При единичном ступенчатом воздействии (рис. 1-5, а) входная величина мгновенно возрастает от нуля до единицы и далее остается неизменной. Единичное ступенчатое воздействие, или единичная ступенчатая функция 1(t) описывается выражением:

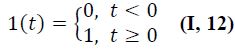
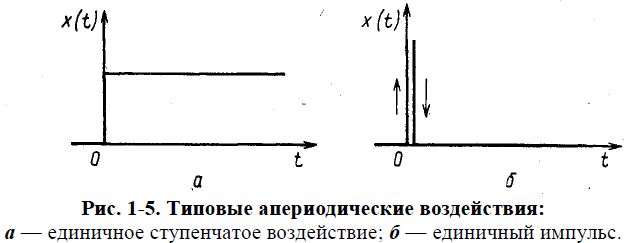
Импульс, величина которого равна бесконечности, длительность — нулю, а площадь — единице (рис. 1-5,б) называется единичным импульсом. Его аналитическое выражение называют единичной импульсной функцией, или дельта-функцией, и обозначают через δ(t).

Дельта-функцию при условии, что записывают так:

Переходная характеристика — это частный случай временной характеристики при подаче на вход элемента или системы единичного ступенчатого возмущения. Ее обозначают через h(t). Таким образом, если x_вх(t)=1(t), то x_вых(t)=h(t).

Импульсная переходная характеристика — это временная характеристика при подаче на вход элемента или системы единичного импульса. Ее аналитическим выражением является импульсная переходная функция, или весовая функция (функция веса) w(t). Следовательно, x_вых(t)= w(t) при x_вх(t)= δ(t). Между переходной и весовой функциями линейных звеньев наблюдается зависимость, аналогичная вышеприведенной: