15. Регуляторы двухпозиционные идеальные и с зоной неоднозначности. Статические характеристики: математическое описание и графики. Область применения.

Позиционные регуляторы (Пз-регуляторы). Позиционными, или релейными, называют регуляторы, у которых при изменении на входе выходная величина может принимать только определенные, заранее известные значения. Переход от одного из этих значений к другому происходит очень быстро, практически мгновенно. Они просты по конструкции, надежны в работе, несложны в обслуживании и при настройке.

Наибольшее распространение получили двухпозиционные регуляторы, у которых выходная величина может принимать только два значения: минимальное или максимальное. Иногда такие регуляторы называют регуляторами типа «открыто» — «закрыто».

Статические характеристики идеального двухпозиционного регулятора и регулятора с зоной нечувствительности (т. е. при неоднозначной характеристике) приведены на рис. III-3. Если текущее значение входной величины идеального регулятора у_т меньше заданного и₃ = у₀, то его выходная величина х_р принимает минимальное значение, равное нулю. Если же у_т>и₃, то выходная величина х_р принимает максимальное значение х_{р ,max} (рис. III-3,а). При изменении текущего значения регулируемой величины в момент перехода им заданного значения выходная величина Пз-регулятора быстро изменяется от одного крайнего положения до другого. Таким образом, работа идеального (с однозначной характеристикой) Пз-регулятора может быть представлена в виде:

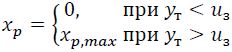
У регулятора с зоной нечувствительности выходная величина х изменяется от 0 до значения х_р,max при у = и₃+δy_t /2 и от значения х_р,мах до нуля — при у = и₃ - δy_t /2 (рис. 7III-3,б). Характеристика такого регулятора выражается следующим образом

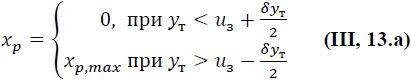
В интервале

величина х_р может принимать два значения (0 и x_p,mах) в зависимости от предыдущих значений у. Переход с нижней ветви на верхнюю осуществляется при условиях:

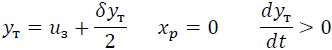
а с верхней ветви на нижнюю — при условиях

На рис. III-3, в и г показаны статические характеристики тех же регуляторов в относительных величинах. Для идеального регулятора они могут быть записаны в виде:

а для регулятора с зоной нечувствительности

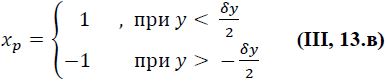
Условие перехода х снизу вверх принимает вид

а сверху вниз

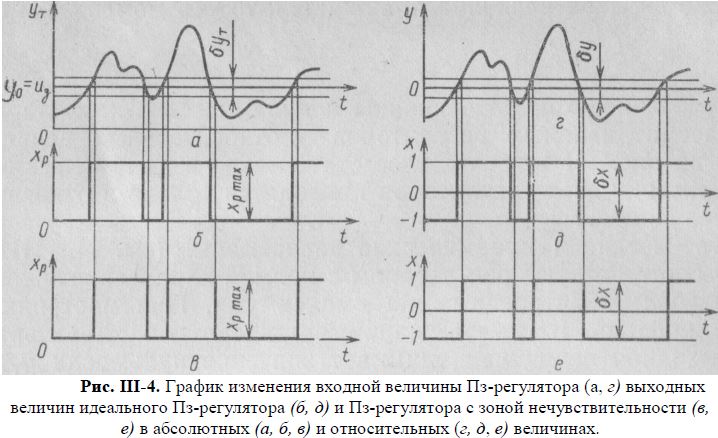
При непрерывном произвольном изменении технологической величины у_т (рис. III-4, а) выходная величина x_р Пз-регулятора с идеальной статической характеристикой принимает другое значение только при переходе у_т заданного значения и₃, т. е. в момент изменения знака отклонения у_т—и₃. Пз-регулятор не учитывает, удаляется ли регулируемая величина от заданного значения или приближается к нему, а также изменяется ли она с большой или малой скоростью (рис. III -4,б).

При непрерывном возрастании входной величины выходная величина Пз-регулятора с зоной нечувствительности (рис. III-4, в) принимает другое значение в момент, когда

если же входная величина понижается, то — в момент, когда

Изменение входной величины и динамические характеристики рассматриваемых регуляторов в относительных величинах даны на рис. III-4, г—е. Далее статические и динамические характеристики всех регуляторов приводятся только в относительных величинах.

Статические и динамические зависимости (см. рис. III-3 и III-4) соответствуют регуляторам с прямой характеристикой или регуляторам, настроенным на «максимум». При настройке их на «минимум», в случае, например, идеальной характеристики, выходная величина принимает значение нуль, если у_т>и₃, и значение х_{р мах}, если у_т<и₃. Статическая характеристика такого регулятора в относительных величинах записывается следующим образом:

Примерами Пз-регуляторов или двухпозиционных устройств могут служить электроконтактный термометр, биметаллический сигнализатор температуры, электроконтактный манометр, пневматическое реле и др.

16. Пропорционально-интегрально-дифференциальные регуляторы. Уравнения динамики для регуляторов с зависимыми и независимыми параметрами настройки. Переходные характеристики. Параметры настройки. Область применения.

Пропорционально-дифференциальные и пропорционально интегрально дифференциальные регуляторы (ПД- и ПИД - регуляторы). В ряде случаев качество регулирования можно повысить введением в закон регулирования составляющей, пропорциональной первой производной или скорости изменения входной величины регулятора. Эта дифференцирующая составляющая (Д-составляющая) формируется при помощи дополнительного устройства.

Уравнения динамики ПД- и ПИД - регуляторов имеют вид

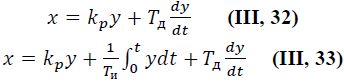
где k_p— коэффициент передачи регулятора; Т_и — время интегрирования; T_д — время дифференцирования.

ПД - регулятор имеет два параметра настройки: предел пропорциональности δ и время дифференцирования T_д. ПИД - регулятор имеет три параметра настройки: предел пропорциональности δ, время интегрирования T_и и время дифференцирования T_д. Воздействие входной величины этих регуляторов на выходную повышается с уменьшением предела пропорциональности уменьшением времени интегрирования T_и и увеличением времени дифференцирования Tд.

При наличии Д-составляющей выходная величина регулятора х изменяется с некоторым опережением относительно входной величины, пропорциональным скорости ее изменения dy/dt. С уменьшением производной dy/dt опережающее действие регулятора также уменьшается и полностью прекращается при у = const; поэтому их называют регуляторами с опережением, или предварением.

Влияние Д-составляющей в ПД- и ПИД - регуляторах одинаково, поэтому далее будем рассматривать только ПД - регуляторы.

Влияние введения Д-составляющей в пропорциональный закон регулирования иллюстрируется графиком, приведенным на рис. III-13, где показаны изменение пропорциональной х_П и дифференциальной х_д составляющих, а также пропорционально-дифференциальной х_пд составляющей, т. е. ПД - закона регулирования при непрерывном изменении входной величины у.

В случае применения П - регулятора при одинаковом отклонении регулируемой величины от заданного значения (точки А и В) величина воздействия на объект будет одинакова независимо от того, удаляется ее значение от заданного или приближается к нему. Для повышения же качества регулирования воздействие регулятора должно было бы быть большим в случае удаления регулируемой величины от заданного значения, чем при противоположном изменении. Это требование выполняется при введении в закон регулирования Д-составляющей; при нахождении регулируемой величины в точке А выходная величина ПД - регулятора больше

Р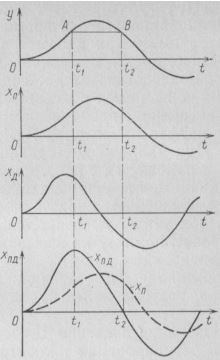 ис. III-13. График, иллюстрирующий влияние введения дифференциальной составляющей в пропорциональный закон регулирования.

(воздействия П- и Д-составляющих регулятора складываются), чем в точке В (воздействия П- и Д-составляющих регулятора вычитаются).

При наличии в законе регулирования Д-составляющей регулятор реагирует и на изменения скорости входной величины, т.е. на интенсивность ее изменения; такой регулятор вступает в работу быстрее, чем П - регулятор. Введение в закон регулирования воздействия по производной приводит к усилению влияния регулятора на переходный процесс, при этом сокращается время переходного процесса и уменьшаются колебания регулируемой величины.

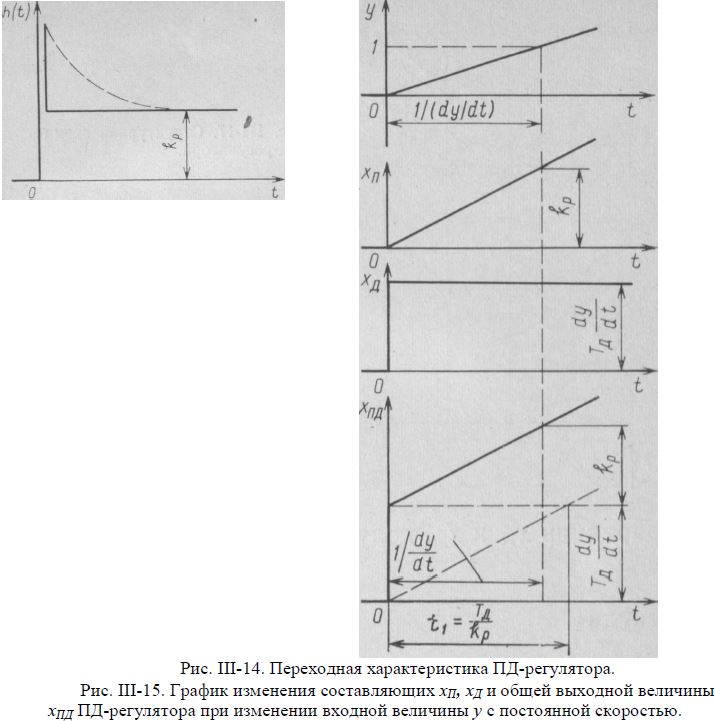
Переходная характеристика ПД - регулятора h(t) приведена на рис. III-14. Она отличается от переходной характеристики П - регулятора большим изменением выходной величины сразу же после изменения величины у. С течением времени отклонение х уменьшается, и величина х становится постоянной и равной х_п в соответствии со значением предела пропорциональности П-составляющей регулятора. Физически действие предварения можно представить как временное уменьшение действия обратной связи регулятора.

Динамическая характеристика ПД - регулятора для случая, когда входная величина изменяется с постоянной скоростью, приведена на рис. III-15. Для сравнения там же приведена аналогичная характеристика для П - регулятора. Выходные величины П- и ПД - регуляторов изменяются с одинаковой скоростью, равной k_p*dy/dt, но при ПД - регуляторе выходная величина всегда на T_д*dy/dt больше, чем при П - регуляторе. По сравнению с х_П выходная величина x_ПД достигает тех же значений с опережением, равным T_д/k_p. По графикам (см. рис. III-15) можно найти время дифференцирования T_д. Обозначим через t₁ время, в течение которого величина x_П достигает ступенчатого изменения величины х_Д, равного

Изменение х_П за время t₁ равно

Приравняв х_П и х_Д, получим

Откуда

Таким образом, время дифференцирования T_д—это отрезок времени, на который выходная величина ПД - регулятора x_пд опережает его пропорциональную составляющую x_п при изменении входной величины с постоянной скоростью и при условии, что коэффициент передачи регулятора k_p равен единице.

Графики, приведенные на рис. III-16, позволяют сравнить работу ПД- и П - регуляторов при колебательном изменении входной величины у. На рисунке показано изменение выходной величины регулятора во времени под действием только П-составляющей (выходная величина П - регулятора) х_п и только Д-составляющей х_д. Отметим, что максимальное отклонение величины x_д наблюдается при максимальной скорости изменения параметра у. Зависимость х_пд (выходная величина ПД - регулятора) получена путем алгебраического сложения ординат кривых x_п и х_д. Из рисунка видно, что изменение величины х_пд опережает изменение величины х_п, а следовательно, и изменение параметра у. Это еще раз подтверждает, что в замкнутом контуре регулирования при отклонении регулируемой величины от заданного значения ПД - регулятор вступает в работу раньше, чем П - регулятор.

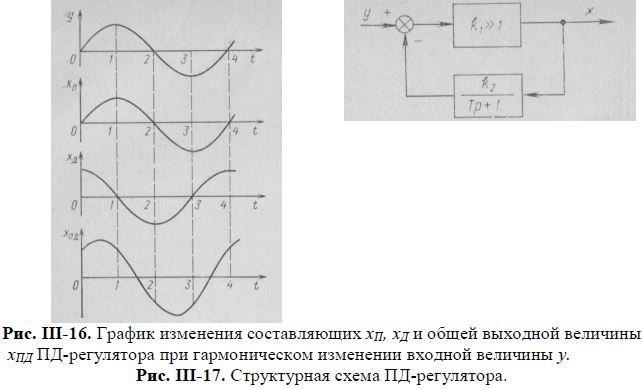
Структурная схема ПД - регулятора приведена на рис. III-17. Она состоит из усилительного звена с очень большим коэффициентом передачи (k>>1) и апериодического звена 1-го порядка, установленного в цепи отрицательной обратной связи. Передаточная функция W(p) такой системы, в соответствии с равенством (I,49) она равна

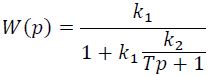
Разделив числитель и знаменатель полученного выражения на k₁ и пренебрегая в знаменателе слагаемым 1/k₁ получим

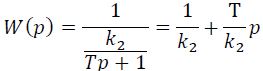
Вводя новые обозначения k_р=1/k₂ и T_д = T/k₂, окончательно находим

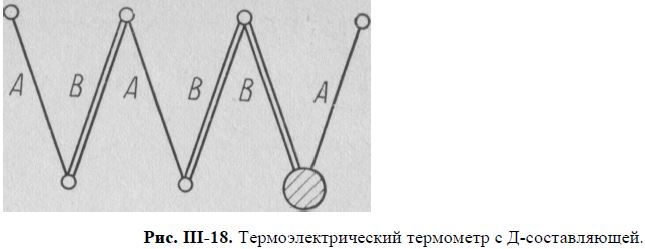
Дифференциальная составляющая может быть введена в закон регулирования и с помощью других элементов системы, например, термоэлектрического термометра с Д-составляющей (рис. III-18), состоящего из трех термопар, две из которых включены последовательно, а третья — встречно. Масса рабочего спая третьей термопары значительно больше, чем у первых двух. При тепловом равновесии все три спая имеют одинаковые температуры и термопары развивают одинаковые ТЭДС; при этой суммарная ТЭДС такой цепи равна ТЭДС одной термопары. При изменении температуры две первые термопары практически сразу начнут менять свою ТЭДС, а изменение ТЭДС третьей термопары будет отставать от них тем больше, чем больше различие масс рабочих спаев термопар и скорость изменения температуры. В частности, при возрастании температуры с постоянной скоростью ТЭДС цепи термопар будет больше, чем ТЭДС одной термопары.

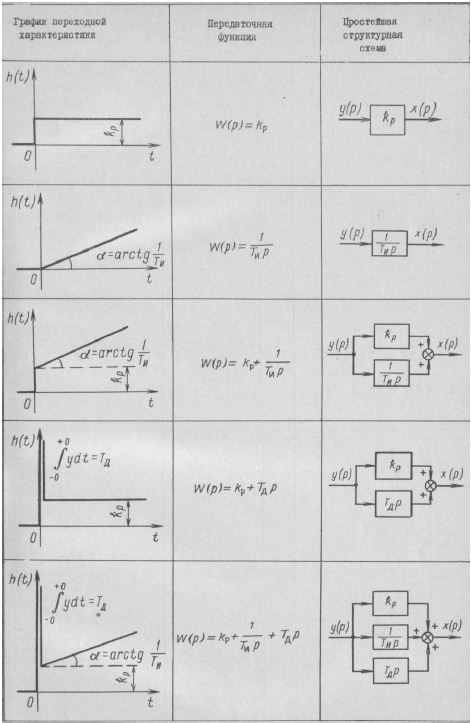
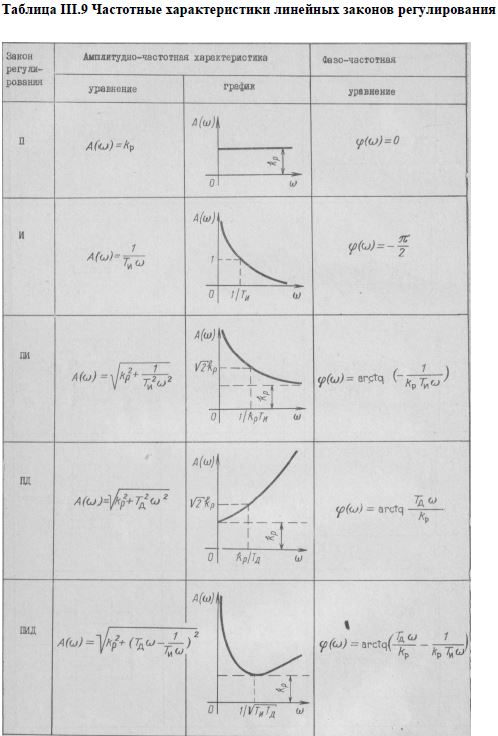
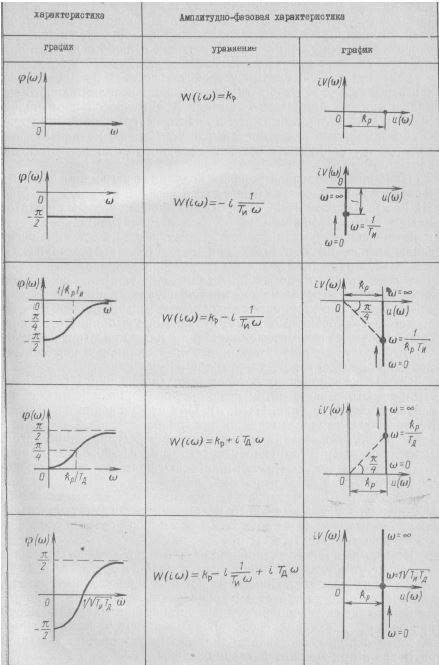
Уравнения динамики, переходные характеристики и их графики, передаточные функции и простейшие структурные схемы изложенных выше линейных законов регулирования приведены в табл. III.8, а их частотные характеристики — в табл. III.9.