10

Глава 5. Функции нескольких переменных

5.1. Пространство и функции нескольких переменных

Как и в главе 1, здесь под будем понимать множество, элементами которого являются всевозможные упорядоченные наборы из n действительных чисел , т.е. n-мерное линейное пространство. В частности, – числовая прямая, – координатная плоскость , - трехмерное геометрическое пространство . В линейном евклидовом пространстве определены линейные операции над элементами пространства, скалярное произведение элементов и , норма (длина) элемента , угол и расстояние между элементами и .

Пусть точка и . Множество всех точек для которых выполняются неравенства

,

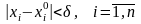называется n-мерным кубом с ребром и с центром в точке . Например, двумерный куб это квадрат со стороной с центром в точке _.

Множество точек , которые удовлетворяют неравенству

называются n-мерным шаром радиуса с центром в точке . Заметим, что n-мерный шар называют также -окрестностью точки в . Это записывается так:

.

Таким образом, одномерный шар есть интервал длиной . Двумерный шар есть круг, для которого верно

или

Множество называется ограниченным, если существует n-мерный шар, содержащий это множество.

Точка множества называется внутренней точкой этого множества, если существует -окрестность содержащаяся в X: .

Множество, каждая точка которого является его внутренней точкой, называется открытым множеством в . Понятно, что пространство является открытым множеством.

Точка называется граничной точкой множества Х, если любая ее окрестность содержит точку, принадлежащую множеству Х и точку не принадлежащую множеству Х. Все граничные точки множества Х называют границей Х и обозначают .

Определение. Пусть множество в , и каждой точке поставлено в соответствие единственное число . В этом случае говорят, что на множестве Х определена числовая функция n переменных (или функция нескольких переменных).

Правило, по которому устанавливается соответствие, обозначают некоторой буквой, например и пишут

или , .

Другими словами функция n переменных есть отображение множества на множество :

, где .

Множество Х является областью определения функции , а называют аргументом или независимой переменной.

Функция называется элементарной, если она может быть задана с помощью конечного числа арифметической операции и суперпозиций элементарных функций одной переменной.

Графиком функции называют множество точек связанных соотношением .

Функция является линейной функцией n переменных и называется гиперплоскостью. Область её определения все точки, принадлежащие . Рассмотрим примеры функций двух и трех переменных.

1. Функция z=ax+by+c определяет в плоскость (система координат Oxyz) , причем в общем виде уравнение плоскости имеет вид

Ax +By +Cz +D=0.

Вектор N(A,B,C) называется нормальным вектором этой плоскости (он перпендикулярен плоскости).

2. Функция геометрически представляет собой поверхность в , которая называется параболоидом. В вертикальных сечениях координатными плоскостями Oxz и Oyz получаются соответственно параболы и . При a=b поверхность называется параболоидом вращения.

3. Функция геометрически представляет собой поверхность в , которая называется эллиптическим конусом. В сечениях этой поверхности плоскостями, параллельными плоскости Oxy,получаются эллипсы. Если a=b, то конус называется круговым.

Определение. Линией уровня функции двух переменных u=f(x,y) называется плоская кривая, которая получается при пересечении поверхности, задаваемой этой функцией и плоскостью, параллельной координатной плоскости Оxy, т.е. уравнение линии уровня имеет вид f(x,y)=C.

Понятие линии уровня широко используется в геодезии, картографии, при описании различных физических полей (температура, давление и т.п.). На плоскости Оxy линии уровня представляю собой семейство непересекающихся кривых, с помощью которых удобно анализировать сложный характер поверхности, описываемой функцией u=f(x,y).

Пример. Найти линии уровня функции u=x² +y² -2x=2y.

Решение. По определению линии уровня имеем x² +y² -2x-2y=С.

или

(x-1)²+(y-1)²=C+2.

Это уравнение описывает семейство окружностей с центром в точке (1,1) радиусами r=

Определение. Поверхностью уровня функции трех переменных u=f(x,y,z) называется поверхность, на которой эта функция имеет постоянное значение, т.е.

f(x,y,z)=С.

Пример. Найти поверхности уровня функции u= x² -2x+y² +2y-z.

Решение. Согласно определению поверхности уровня, имеем

x² -2x+y² +2y-z=С, откуда z=(x-1)² +(y+1)² –C. Следовательно, поверхностями уровня данной функции являются параболоиды вращения с осью x=1, y=-1, параллельной оси Oz , вершины которых лежат в точках с координатами (1,-1,С).