
- •Содержание.
- •Глава I. Обзор предметной области…………………………………………..
- •Глава II. Методические указания для выполнения лабораторных
- •Введение
- •1.1 Кодирование сообщений переданных дискретным источником
- •1.2 Кодирование информации для передачи по каналу с шумом
- •1.3 Кодирование с заданным критерием качества
- •1.5 Секретная связь с системой защиты информации от несанкционированного доступа
- •Глава 2. Практическая часть. Лабораторная работа №1
- •Теоритические сведения
- •Взаимная информация
- •Лабораторная работа №2
- •Теоритические сведения Энтропия
- •Условная энтропия
- •Избыточность
- •Лабораторная работа №6
- •Теоритические сведения
- •Алгоритмы генерации псевдослучайных последовательностей
- •Лабораторная работа №7
- •Теоритические сведения
- •Лабораторная работа №8
- •Теоритические сведения
- •Cодержание отчета Отчет по лабораторной работе должен содержать:
Условная энтропия
Пусть
имеются два статистически независимых
конечных ансамбля символов
.
Пары символов
 с вероятностью
с вероятностью
 – это элементарные символы объединенного
ансамбля
– это элементарные символы объединенного
ансамбля
 с энтропией, вычисляемой по формуле
(6):
с энтропией, вычисляемой по формуле
(6):
|
(1.6) |
Появление
символа
вызывает появление символа
с вероятностью
 .
.
Частная условная энтропия:
|
(1.7) |
Средняя условная энтропия ансамбля при условии, что ансамбль известен:
|
(1.8) |
Свойства условной энтропии:
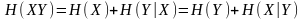 ,
при условии, что
зависимы.
,
при условии, что
зависимы.
Кроме того:
 .
.
 ,
если
независимы.
,
если
независимы. ,
причем равенство только в случае, если
независимы.
,
причем равенство только в случае, если
независимы. .
. .
.
Причем
равенство только в случае, если
условно независимы при всех
 .
.
Далее приводятся формулы для связи средней взаимной информации и энтропии:
 .
.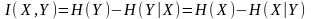 .
. ,
то есть энтропия – это частный случай
функционала средней взаимной информации.
,
то есть энтропия – это частный случай
функционала средней взаимной информации. .
.
Причем равенство нулю возможно тогда и только тогда, когда статистически независимы.
Пример
Вычислить
энтропию
 ,
условную энтропию
,
условную энтропию
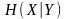 и среднюю взаимную информацию
и среднюю взаимную информацию
 ,
если дано
,
если дано
 двух ансамблей
:
двух ансамблей
:
|
|
|
|
|
0.5 |
0 |
0.5 |
|
0.25 |
0.25 |
0.5 |
|
0.75 |
0.25 |
|
Решение
Найдем
 :
:
|
|
|
|
1 |
0 |
|
0.5 |
0.5 |
Энтропия
 ,
,
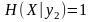 ,
,
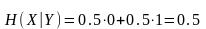 ,
,
 .
.
Средняя
взаимная
информация:
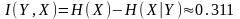 .●
.●
Избыточность
Считают, что имеется избыточность, если количество информации, содержащейся в сигнале (энтропия сигнала), меньше того количества, которое этот сигнал мог бы содержать по своей физической природе.
Пусть
сигнал длиной
символов содержит количество информации
 ;
кроме того, наибольшее количество
информации, которое может содержаться
в данном сигнале с учетом наложенных
ограничений (таких, как основание кода,
заданная средняя мощность сигнала и
т.п.), равно
;
кроме того, наибольшее количество
информации, которое может содержаться
в данном сигнале с учетом наложенных
ограничений (таких, как основание кода,
заданная средняя мощность сигнала и
т.п.), равно
 .
Тогда количественной мерой избыточности
является величина:
.
Тогда количественной мерой избыточности
является величина:
|
(1.9) |
Причина избыточности – статистические связи между символами сигнала и не экстремальность распределения вероятностей отдельных символов. Введение избыточности приводит к удлинению сигнала, но повышает его информационную устойчивость при воздействии помех.
Статистические связи между сигналами наблюдаются в случае ИДС с памятью: здесь вероятность выдачи им очередного элемента сообщения зависит от того, какие элементарные сообщения были выданы ранее.
Примером ИДС с памятью является источник связного русского текста, где в качестве элементарных сообщений выступают буквы. Сочетание ‘ар’ будет встречаться чаще, чем ‘аъ’.
Избыточность показывает, какая доля максимально возможной при заданном объеме алфавита неопределенности (энтропии) не используется источником.
Пример
Дан
ансамбль:
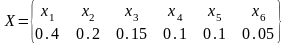 .
.
Символы в последовательности независимы. Найти энтропию источника и вычислить избыточность.
Решение
Энтропия:
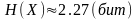 .
.
Избыточность
за счет не оптимальности (не равно
вероятности) распределения элементарных
сообщений в источнике:
 ,
где
,
где
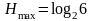 .●
.●
Индивидуальные задания.
Пример 1
Алфавит
источника состоит из трех букв
 .
Определить энтропию на 1
букву текста
.
Определить энтропию на 1
букву текста
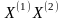 для следующих случаев:
для следующих случаев:
(а)
появлениебукв
не равновероятно:
 ,
а символы в последовательности на выходе
источника статистически зависимы.
Условные вероятности переходов
,
а символы в последовательности на выходе
источника статистически зависимы.
Условные вероятности переходов
 заданы таблицей:
заданы таблицей:
i – индекс предыдущей буквы |
j – индекс последующей буквы |
||
|
1 |
2 |
3 |
1 |
0.4 |
0.2 |
0.4 |
2 |
0.0 |
0.6 |
0.4 |
3 |
0.3 |
0.0 |
0.7 |
(б) вероятности букв те же, что и в пункте (а), но символы независимы;
(в) символы в последовательности независимы, а вероятности букв одинаковы.
Вычислить избыточность источника для случаев (а) и (б).
Контрольные вопросы:
Дать определение энтропии, условной энтропии, избыточности.
Свойства энтропии.
3.Свойства условной энтропии.

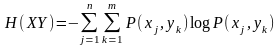 .
.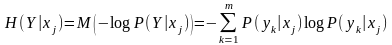 .
.

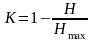 .
.