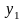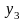- •Содержание.
- •Глава I. Обзор предметной области…………………………………………..
- •Глава II. Методические указания для выполнения лабораторных
- •Введение
- •1.1 Кодирование сообщений переданных дискретным источником
- •1.2 Кодирование информации для передачи по каналу с шумом
- •1.3 Кодирование с заданным критерием качества
- •1.5 Секретная связь с системой защиты информации от несанкционированного доступа
- •Глава 2. Практическая часть. Лабораторная работа №1
- •Теоритические сведения
- •Взаимная информация
- •Лабораторная работа №2
- •Теоритические сведения Энтропия
- •Условная энтропия
- •Избыточность
- •Лабораторная работа №6
- •Теоритические сведения
- •Алгоритмы генерации псевдослучайных последовательностей
- •Лабораторная работа №7
- •Теоритические сведения
- •Лабораторная работа №8
- •Теоритические сведения
- •Cодержание отчета Отчет по лабораторной работе должен содержать:
Глава 2. Практическая часть. Лабораторная работа №1
Тема:«Собственная информация и взаимная информация»
Цель работы:
1.Ознакомление со структурой и принципом вычисления взаимной и собственной информаций.
2.Вычисление взаимной информации.
3. Составление отчета по лабораторной работе.
Теоритические сведения
Собственная
информация сообщения
сообщения
 ,
выбираемого из дискретного ансамбля
,
выбираемого из дискретного ансамбля
 – это:
– это:
|
(1.1) |
|
|
Если
 ,
то количество информации измеряется в
битах;
,
то количество информации измеряется в
битах;
 – натах;
– натах;
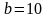 –ди/хартли
(Хартли впервые предложил эту формулу
в виде
–ди/хартли
(Хартли впервые предложил эту формулу
в виде
 в 1928 г.).
в 1928 г.).
Свойства собственной информации:
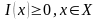 .
.Монотонность: если
 ,
то
,
то
 .
.Аддитивность: (для независимых сообщений)
 .
.
Пример
Дан
ансамбль:
 .
Кодирование будем производить, используя
0
и 1.
.
Кодирование будем производить, используя
0
и 1.

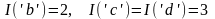 .●
.●
Видно, что чем выше вероятность появления символа в сообщение (чем чаще он появляется), тем меньшим числом бит его надо кодировать, чтобы сэкономить на длине закодированного сообщения.
Таким образом, собственная информация характеризует степень неожиданности появления конкретного сообщения.
Пример
Определить собственную информацию, содержащуюся в изображении, при условии, что оно состоит из 500 строк по 500 элементов в каждой строке. Яркость каждого элемента передается 8 уровнями. Яркости различных элементов независимы.
Решение
Случайная
величина
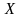 – яркость одного элемента изображения.
– яркость одного элемента изображения.
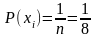 .
.
 .
Изображение содержит
.
Изображение содержит
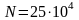 элементов. Так как яркости элементов
независимы, то
элементов. Так как яркости элементов
независимы, то
 .●
.●
Пример
На
экране радара
 полос; изображение появляется в виде
яркой отметки. Все положения равновероятны.
Определить количество собственной
информации, содержащейся в сообщениях:
(а) объект находится в 46
квадранте, (б) объект находится в 5-ой
горизонтальной строке.
полос; изображение появляется в виде
яркой отметки. Все положения равновероятны.
Определить количество собственной
информации, содержащейся в сообщениях:
(а) объект находится в 46
квадранте, (б) объект находится в 5-ой
горизонтальной строке.
Решение
(а)
 .
.
(б)
 .●
.●
Взаимная информация
Рассмотрим
два ансамбля сообщений:
 .
.
 – ансамбль сообщений на входе системы,
– ансамбль сообщений на входе системы,
 – на выходе. Естественно, что они
зависимы.
– на выходе. Естественно, что они
зависимы.
В
результате опыта (приема символа
 )
апостериорная вероятность появления
символа
)
апостериорная вероятность появления
символа
 изменяется в сравнении с априорной.
Тогда количество информации символа
сообщения
,
доставляемое символом
,
можно определить как логарифмотношения
апостериорной вероятности к априорной:
изменяется в сравнении с априорной.
Тогда количество информации символа
сообщения
,
доставляемое символом
,
можно определить как логарифмотношения
апостериорной вероятности к априорной:
|
(1.2) |
Это и есть определение взаимной информации.
Свойства взаимной информации:
 .
.
Если
 ,
то считается, что наступление события
делает наступление события
менее
вероятным, чем оно было априори до
наблюдения
.
,
то считается, что наступление события
делает наступление события
менее
вероятным, чем оно было априори до
наблюдения
.
 ,
,
 – взаимная информация не превышает
свою собственную.
– взаимная информация не превышает
свою собственную.
При
данном взаимная информация достигает своего
максимума, когда принятый символ
однозначно определяет переданный символ
.
взаимная информация достигает своего
максимума, когда принятый символ
однозначно определяет переданный символ
.
При
этом
 и это максимальное значение равно
и это максимальное значение равно
 ,
то есть собственной информации,
определяемой только априорной вероятностью
символа
.
,
то есть собственной информации,
определяемой только априорной вероятностью
символа
.
Симметрия:
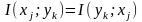 .
Информация, содержащаяся в
относительно
,
равна информации, содержащейся в
относительно
.
Поэтому
.
Информация, содержащаяся в
относительно
,
равна информации, содержащейся в
относительно
.
Поэтому
 – это именно взаимная
информация.
– это именно взаимная
информация.Аддитивность:
 ,
только при условии, что ансамбли
независимы от
,
только при условии, что ансамбли
независимы от .
.
Информация, содержащаяся в реализации принятого сигнала относительно ансамбля передаваемых сообщений , определяется следующей формулой:
|
(1.3) |
Наконец,
средняя взаимная информация между
ансамблем принимаемых сигналов
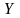 и ансамблем передаваемых сообщением
определяется
формулой (4):
и ансамблем передаваемых сообщением
определяется
формулой (4):
|
(1.4) |
то есть то количество информации, которое содержится в среднем в ансамбле принимаемых символов относительно ансамбля передаваемых символов .

Пример.
По
дискретному каналу передаются сообщения
 и
и
 .
Вследствие шумов на выходе канала
появляются сигналы
.
Вследствие шумов на выходе канала
появляются сигналы
 .
Вероятности их совместного появления
.
Вероятности их совместного появления
 заданы
в таблице:
заданы
в таблице:
|
|
|
|
|
1/4 |
1/16 |
1/8 |
|
1/8 |
3/16 |
1/4 |
Необходимо
найти взаимную информацию
 и
и
 .
.
Решение
 .
.
 ,
,
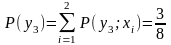 .
.
 .
Значит,
.
Значит,
 .
.
Аналогично:
 .●
.●
П ример
ример
Дан ансамбль сообщений:
|
|
|
|
|
|
|
|
|
1/2 |
1/4 |
1/8 |
1/32 |
1/32 |
1/32 |
1/32 |
Код |
001 |
010 |
100 |
011 |
101 |
110 |
111 |
Сообщение поступило в кодер. Вычислить дополнительную информацию об этом сообщении, доставляемую каждым последующим символом на выходе кодера.
Решение
Найдем
взаимную информацию, содержащуюся в
первом кодовом символе ‘1’
относительно сообщения
:
 (см. следующий рисунок).
(см. следующий рисунок).
1 |
? |
? |
 ,
где
– это гипотеза о том, что было передано
4-ое
сообщение.
,
где
– это гипотеза о том, что было передано
4-ое
сообщение.
 – это
вероятность появления ‘1’ на первом
месте в кодовом слове.
– это
вероятность появления ‘1’ на первом
месте в кодовом слове.
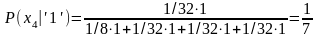 .
.
Таким
образом,
 .
.
Информация, содержащаяся во втором кодовом символе ‘0’ при условии, что первый кодовый символ равен ‘1’:
 ,
где
,
где
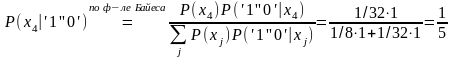 .
.
1 |
0 |
? |
Информация, содержащаяся в третьем кодовом символе ‘1’ при условии, что первые два кодовых символа равны ‘10’:
 .
.
1 |
0 |
1 |
Так как сообщение и кодовые слова однозначно связаны, то
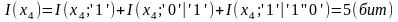 .
.
По
свойству 2) получаем тот же ответ:
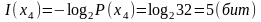 .●
.●
Заметим, что среднее значение, или математическое ожидание, вычисленные по ансамблю, будут характеристикой информативности всего ансамбля: для этого вводят понятие энтропии.
Индивидуальные задания для выполнения:
1.Пример1
По дискретному каналу передаются сообщения и х3 .Вследствие шумов на выходе канала появляются сигналы и у4.Вероятности их совместного появления заданы в таблице:
|
|
|
|
у4 |
|
1/4 |
1/16 |
1/8 |
2/16 |
|
1/8 |
3/16 |
1/4 |
1/2 |
х3 |
2/4 |
2/8 |
3/24 |
1/24 |
Необходимо найти взаимную информацию , иI (х3;у4)
2. Пример2
Исходя из этой же таблицы найти взаимную информацию, I( ; ), I( ; ) и I(х3; ) .
3.Пример3
Дан ансамбль сообщений:
|
|
|
|
|
|
|
|
|
1/2 |
1/4 |
1/8 |
1/16 |
1/32 |
1/64 |
1/32 |
Код |
001 |
010 |
100 |
011 |
101 |
110 |
111 |
Сообщение поступило в кодер. Вычислить дополнительную информацию об этом сообщении, доставляемую каждым последующим символом на выходе кодера.
Контрольные вопросы:
Дать определение собственной и взаимной информации.
Свойства взаимной информации.
Свойства собственной информации.

 .
. .
.