1.2 Кодирование информации для передачи по каналу с шумом

Помехоустойчивые коды – это коды, позволяющие обнаружить и (или) исправить ошибки в кодовых словах, которые возникают припередачи по каналам связи. Эти коды строятся таким образом, что для передачи сообщения используется лишь часть кодовых слов, которые отличаются друг от друга более, чем в один символ. Эти кодовые слова называются разрешенными, все остальные не используются и называются запрещенными.

Теорема Шеннона (о кодировании в дискретных каналах с шумом).

Пусть пропускная способность канала , скорость создания информации , где 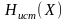– энтропия источника, – частота следования символов источника.

1. Прямая теорема.

Если скорость создания информации 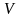источником на входе зашумленного канала без памяти с пропускной способностью такова, что 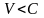, то существует такой код, при котором вероятность ошибки на приемном конце сколь угодно мала, а скорость передачи информации сколь угодно близка к скорости её создания.

2. Обратная теорема.

Если 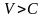, то никакой код не может сделать вероятность ошибок на приемном конце сколь угодно малой и достигнуть надежности, меньшей, чем , а скорость передачи информации сколь угодно близкой к скорости её создания. Основной способ повышения помехоустойчивости системы передачи информации – разумное введение избыточности в передаваемый сигнал .

Помехозащитные коды делятся на две группы:

1. Код с исправлением ошибок имеет цель восстановить с вероятностью близкой к единице посланное сообщение.

2. Код с обнаружением ошибок имеет цель выявить с вероятностью близкой к единицы наличие ошибок.

Введем основные параметры помехоустойчивых кодов:

• Расстояние Хэмминга (кодовое расстояние между двумя кодовыми словами) – число позиций, в которых два кодовых двоичных слова отличаются друг от друга.

• Кодовое расстояние кода – наименьшее расстояние Хэмминга между различными словами кода.

Считают, что в канале произошла -кратная ошибка, если кодовое слово на выходе канала отличается от кодового слова на входе ровно в символах (то есть ).Среди всех корректирующих кодов наибольшее применение нашли систематические коды. Систематическим кодом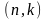 называется двоичный корректирующий код.

1.3 Кодирование с заданным критерием качества

Кодирование источников при заданных ограничениях на точность восстановления декодером - одно из наиболее актуальных разделов в теории информации.

Такие методы сжатия сегодня востребованы во многих областях обработки, хранения и передачи мультимедиа данных.

В случае, когда кодирование источника осуществляется таким образом, что закодированные сообщения восстанавливаются с некоторой ошибкой, не большей заданного значения, говорят, что имеет место кодирование источника с заданным значением критерия качества (или просто с критерием качества).

Рассмотрим несколько примеров критериев качества.

а) называют вероятностным критерием качества.

б) называют квадратичным критерием качества.

При кодировании источника с критерием качества основным показателем эффективности кода так же, как и при безошибочном кодировании источника, является скорость кодирования.

Таким образом, среднее количество двоичных символов, требуемое для кодирования источника с критерием качества, даже при нулевой ошибке можно уменьшить по сравнению с кодированием в отсутствии критерия качества.

Линейным блоковым (n, k) кодом называется множество последовательностей длины 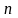над полем Галуа , называемых кодовыми словами. Это поле характеризуется тем, что сумма двух кодовых слов является кодовым словом и произведение любого кодового слова на элемент поля – также кодовое слово.

Если , то линейный код называется групповым, так как кодовые слова образуют математическую структуру, называемую группой. При формировании данного кода линейной операцией является сумма по модулю два ( ).

Основные свойства линейных кодов:

1. Если 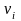– это кодовое слово, то: .

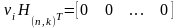2. Произведение некоторого кодового слова с ошибкой на 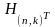даст синдром : .

3. .

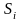4. Кодовое расстояние -кода равно минимальному числу линейно зависимых столбцов .

5. Произведение информационного слова на даст кодовое слово.

6. Два кода называются эквивалентными, если их порождающие матрицы отличаются только перестановкой столбцов и элементарными операциями над строками.

7. Кодовое расстояние любого линейного -кода удовлетворяет неравенству 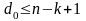(граница Сингтона). Если выполняется строгое равенство, то данный код называется кодом с максимальным расстоянием.

8. Граница Плоткина для минимального количества контрольных разрядов: 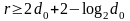при .