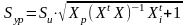Хід роботи

Для множинної лінійної регресії має місце стохастична лінійна залежність випадкового показника Y від декількох факторів X₁, . X₂, …, X_m, яку можна представити моделлю:

,

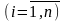
Де п кількість вимірювань, т кількість факторів,

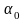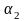, , , …, – параметри моделі,

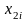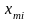, , …, та 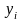– значення факторів та показника для деякого і-того вимірювання,

випадкове відхилення від «лінії регресії».

Задача регресійного аналізу полягає у тому, щоби визначити параметри регресії

,

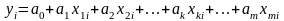встановити адекватність лінійної моделі, знайти довірчу зону регресії, обчислити прогнозоване значення показника та його довірчий інтервал. Таку задачу розв’язують методом найменших квадратів у матричній формі. Здобуті МНК значення параметрів , , 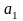, …, 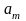– є статистичними оцінками справжніх невідомих параметрів моделі.

Матрична форма моделі має вид:

або

Y=XA+U

Таким чином маємо матриці:

– показника 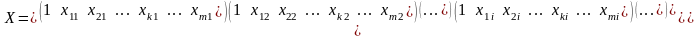– факторів

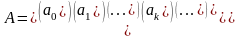– параметрів регресії 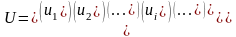– залишків

Матрицю факторів доповнює перший стовпчик із значеннями фіктивного фактору Х₀, які завжди дорівнюють 1.

Оператор оцінювання параметрів знаходимо за формулою:

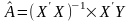
Коефіцієнт детермінації обчислюють в матричній формі:

або

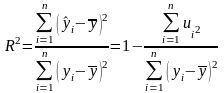
– середнє значення показника.

Множинний коефіцієнт кореляції

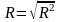
Критерієм тесту на адекватність моделі вибирають F- розподіл Фішера:

Розрахункове значення порівнюють із табличним 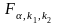. У випадку 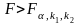– із значимістю α модель вважають адекватною. Тут k₁=m, та k₂=n–m–1 відповідні ступені вільності.

Для множинної регресії перевіряють параметри регресії на значущість за допомогою критерію Стьюдента

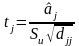
де 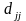- j-й діагональний елемент матриці похибок .

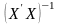Якщо │t_j│>t_α,k, то можна вважати, що вплив відповідного фактора значний (α – рівень значущості, k=n–m–1)

Надійні інтервали базисних даних обчислюють після знаходження дисперсії 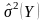за допомогою формули дисперсії для кожного значення вимірювання:

Тут маємо: – рядок матриці факторів,

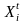транспонований ,

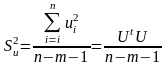– дисперсія залишків.

Надійні інтервали показника знаходять як: 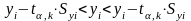, де 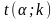– табличне значення функції Стьюдента, α – рівень значущості, k=n–m–1

Дисперсію прогнозованого значення показника, як і для парної регресії, потрібно збільшити на 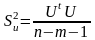щоби врахувати відхилення прогнозу від «лінії» регресії. Отже: 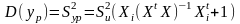, а довірчий інтервал прогнозованого значення показника:

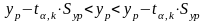, де