Практичне заняття 7.
Тема: Оцінювання параметрів лінійної економетричної моделі з гетероскедастичними залишками.
Мета: Навчитися досліджувати явище гетероскедастичності в економетричних
моделях з використанням EXCEL.
Завдання:
Використовуючи певні критерії перевірити наявність гетероскедастичності.
Оцінити параметри економетричної моделі за допомогою зваженого методу найменших квадратів.
Хід роботи
Для тестування гетероскедастичності використовують декілька способів:
Графічний аналіз
Критерій Бартлетта
Параметричний тест Голдфельда–Квандта
Тест рангової кореляції Спірмена
Тест Глейзера
Тест μ–критерія
Вводиться
гіпотеза, що між факторами X
та показником Y
існує стохастична лінійна залежність
.
Встановимо наявність гетероскедастичності, застосовуючи тест Гольдфельда-Квандта.
Упорядкувати спостереження відповідно до величини елементів незалежної змінної
.Відшукати
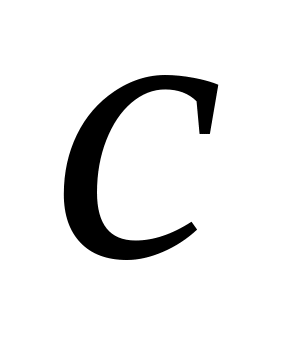спостережень, які містяться в середині
спостережень:
,
де
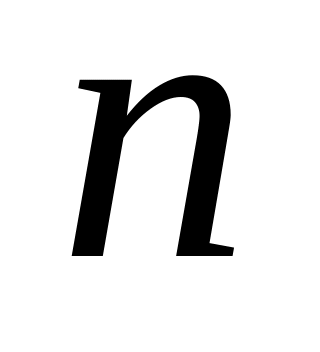- кількість елементів вектора
.
Отримати дві сукупності спостережень.
Побудувати дві економетричні моделі на основі 1МНК за двома утвореними сукупностями спостережень, використовуючи функцію ЛИНЕЙН
Обчислити критерій
,
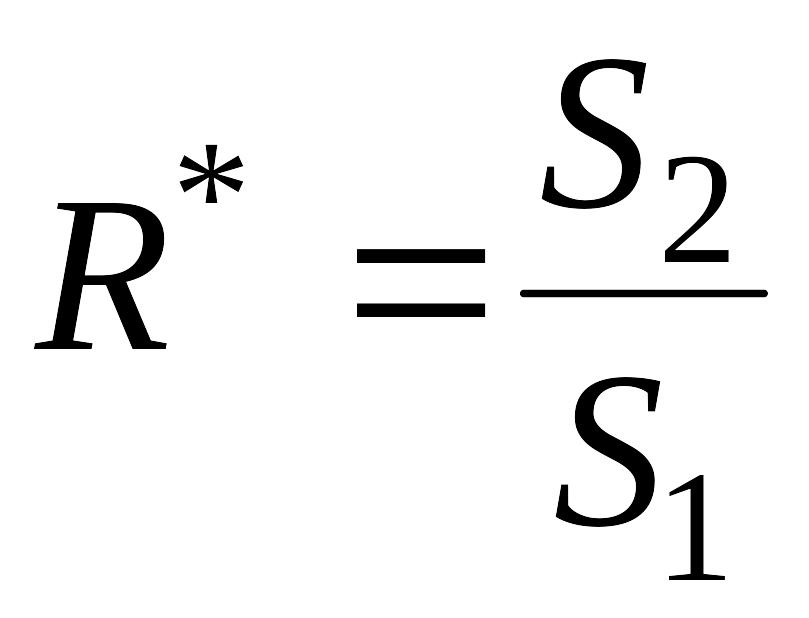який порівнюється з табличним значенням
F-критерію
для ступенів свободи
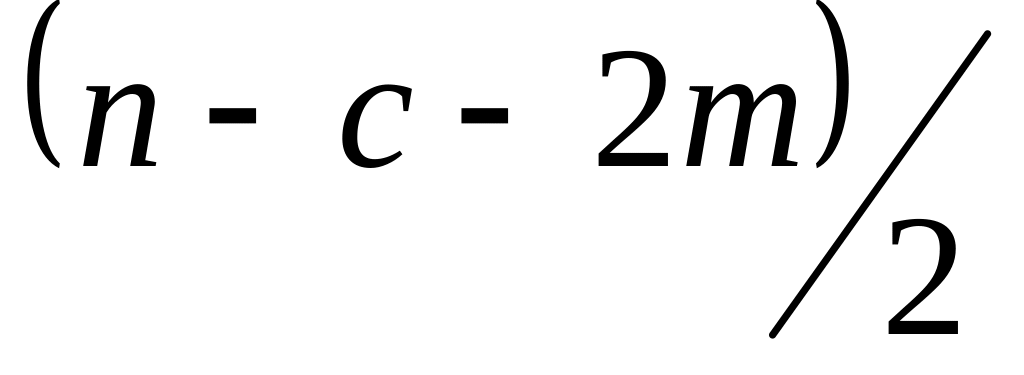і
(m=2) і
вибраного рівня значущості
.
Зробити висновки.
Встановимо наявність гетероскедастичності, застосовуючи тест Глейзера
Оцінити параметри моделі за МНК, використовуючи функцію «ЛИНЕЙН»;
Обчислити абсолютні помилки ABS(uі) для кожного окремого спостереження.
Побудувати моделі
за допомогою функції «ЛИНЕЙН».
Перевірити значущість оцінок параметрів
та
,
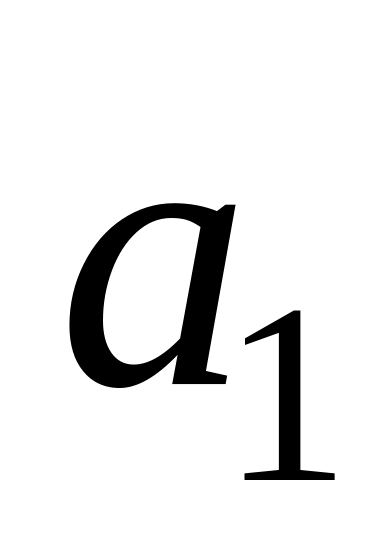використовуючи t-критерій:
.
Зробити висновки.
Якщо встановлено наявність гетероскедастичності, потрібно трансформувати початкову модель таким чином, щоби випадкові помилки мали постійну дисперсію. Спосіб проведення трансформації початкової моделі залежить від форми залежності між дисперсією випадкових величин та значеннями факторних ознак.
Дисперсія
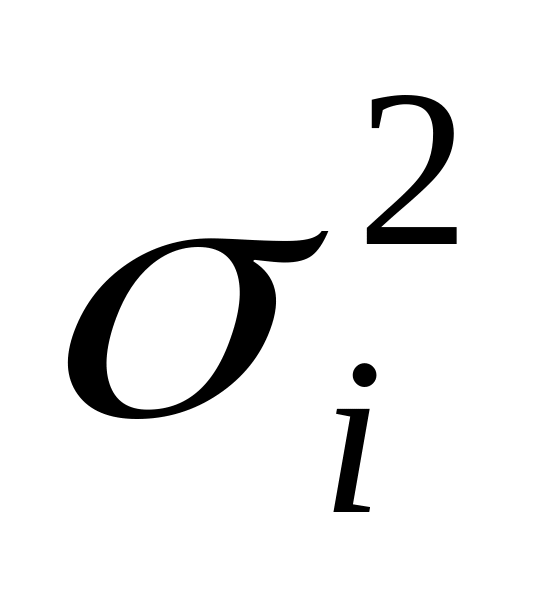пропорційна
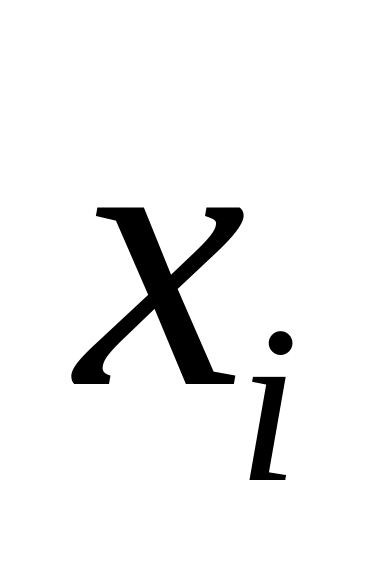
Тоді
трансформація моделі
полягає у діленні лівої правої частин
рівняння на
:
.
За
допомогою функції «ЛИНЕЙН
»
оцінимо параметри моделі з урахуванням
наявності гетероскедастичності.
Дисперсія пропорційна
Трансформація
початкової моделі полягає у діленні
моделі на
.
Взявши у якості зважених змінних Y*
та X*,
та за допомогою функції «ЛИНЕЙН»,або
матричним методом знайти оцінки парної
лінійної регресії А(а0,
а1)
(врахувати, що у відповідних записах
результатів обрахунків а0
та а1
міняються місцями
):
;
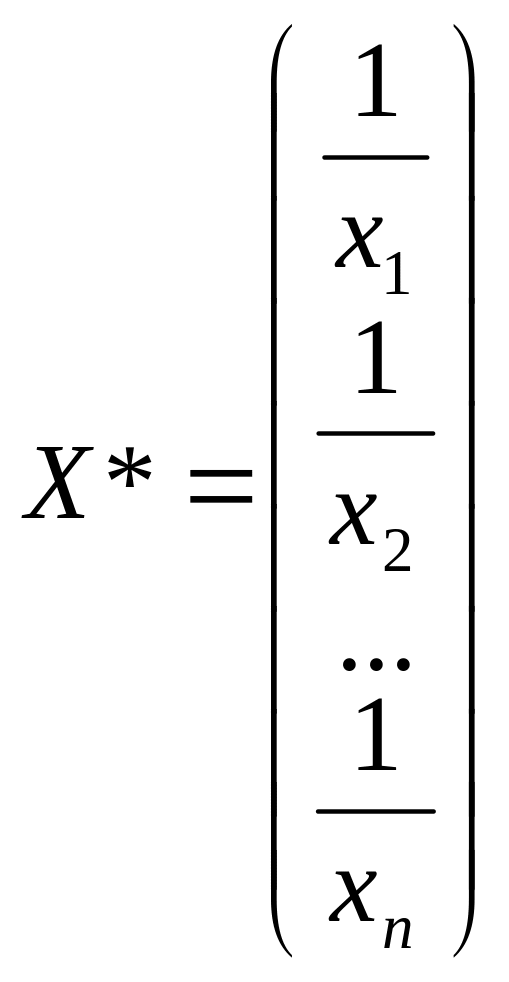або
;
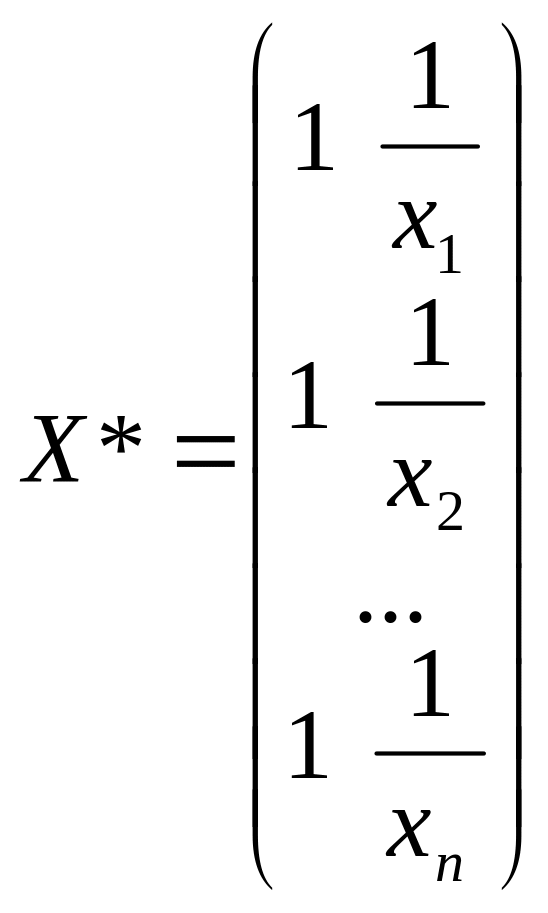
Порівняти результати застосування МНК для вихідних даних без урахування гетероскедастичності та з урахуванням її.
Значення фактора х1
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
25,3 |
22,6 |
8,1 |
8,8 |
6,23 |
10,4 |
1,9 |
12,77 |
27,6 |
13,21 |
8,38 |
6,1 |
9,4 |
13,2 |
9,68 |
78 |
71 |
9,4 |
10,1 |
7,58 |
10,1 |
58 |
10,1 |
76 |
10,45 |
9,4 |
7,4 |
9,1 |
10,9 |
10,1 |
35,5 |
32,4 |
11,4 |
12,1 |
9,1 |
12,1 |
0,2 |
12,1 |
37,4 |
10,19 |
10,28 |
9,4 |
11,1 |
11,6 |
10,98 |
16 |
14 |
15,4 |
16,1 |
13,4 |
16,1 |
62 |
16,1 |
19 |
11,83 |
10,25 |
13,4 |
15,1 |
10,4 |
10,95 |
487 |
347 |
12,3 |
13 |
10,2 |
13 |
14,7 |
13 |
352 |
11,47 |
13,2 |
10,3 |
12 |
10,9 |
13,2 |
11,3 |
11,5 |
7,2 |
7,9 |
5,2 |
7,9 |
180 |
11,98 |
16,5 |
11,74 |
11,28 |
5,2 |
6,9 |
14,2 |
9,98 |
10,5 |
8,6 |
7,9 |
8,6 |
5,9 |
8,6 |
10,8 |
13,19 |
13,6 |
13,46 |
12,49 |
5,9 |
7,6 |
12,2 |
13,19 |
66 |
59 |
10,4 |
11,1 |
8,37 |
11,1 |
43 |
11,1 |
64 |
12,95 |
10,4 |
8,4 |
10,1 |
73,1 |
11,1 |
6,4 |
4,2 |
11,6 |
62,37 |
9,6 |
12,3 |
170 |
12,3 |
9,2 |
13,33 |
11,6 |
9,6 |
11,3 |
63,9 |
12,3 |
76,8 |
63,3 |
62,37 |
52,34 |
60,37 |
10,5 |
88 |
10,5 |
68,3 |
13,77 |
9,8 |
60,37 |
9,5 |
52,6 |
13,5 |
24,1 |
21,7 |
52,34 |
73,48 |
50,14 |
12,1 |
1,2 |
12,1 |
26,7 |
13,81 |
9,81 |
50,34 |
11,1 |
14,2 |
10,51 |
293 |
205 |
73,48 |
49,34 |
71,28 |
11,4 |
521 |
11,4 |
210 |
6,95 |
10,7 |
71,48 |
10,4 |
11,9 |
71,4 |
20,4 |
19,2 |
49,34 |
48,64 |
47,36 |
12,5 |
165 |
12,5 |
24,2 |
14,92 |
67,38 |
47,34 |
11,5 |
35,6 |
70,1 |
52,3 |
48,5 |
48,64 |
67,38 |
46,624 |
13,4 |
681 |
98 |
53,5 |
15,28 |
64,37 |
46,64 |
12,4 |
58,7 |
82,4 |
264,6 |
207,7 |
67,38 |
64,37 |
65,34 |
14,4 |
421 |
67,38 |
212,7 |
40,37 |
86,14 |
65,38 |
13,4 |
67,38 |
93,4 |
95,5 |
89,6 |
64,37 |
86,14 |
62,87 |
15 |
524 |
64,37 |
94,6 |
32,69 |
91,34 |
62,37 |
14 |
64,37 |
101,8 |
9,4 |
8,1 |
86,14 |
91,34 |
84,14 |
15,6 |
563 |
86,14 |
13,1 |
51,62 |
61,37 |
84,14 |
14,6 |
86,14 |
110,5 |
638,1 |
601,3 |
91,34 |
61,37 |
90,34 |
15,4 |
587 |
91,34 |
606,3 |
60,48 |
86,14 |
89,34 |
14,4 |
91,34 |
95,4 |
277 |
254 |
61,37 |
86,14 |
63,37 |
15,3 |
675 |
61,37 |
259 |
75,69 |
91,34 |
59,37 |
14,3 |
61,37 |
130,1 |
868,3 |
831 |
86,14 |
91,34 |
84,14 |
15,2 |
702 |
86,14 |
836 |
61,16 |
19,34 |
84,14 |
14,2 |
86,14 |
125,9 |
522,9 |
491 |
91,34 |
119,34 |
90,35 |
71,4 |
854 |
91,34 |
496 |
35,63 |
78 |
59,34 |
69,4 |
91,34 |
11,4 |
629,9 |
547 |
119,34 |
12,5 |
117,33 |
70,1 |
726 |
119,34 |
552 |
85,14 |
11,8 |
19,34 |
68,1 |
119,34 |
12,5 |
658,7 |
542 |
11,8 |
12,5 |
10,7 |
82,4 |
803 |
67 |
547 |
15,78 |
12,7 |
10,7 |
81,4 |
34 |
13,4 |
687,5 |
345 |
12,7 |
13,4 |
11,7 |
93,4 |
896 |
13,4 |
350 |
16,35 |
13,7 |
11,7 |
92,4 |
41,9 |
11,8 |
876,3 |
791 |
13,7 |
14,4 |
12,3 |
101,8 |
1,9 |
14,4 |
796 |
16,92 |
12,08 |
12,3 |
100,8 |
|
12,5 |
905,1 |
853 |
14,3 |
15 |
12,9 |
|
58 |
15,43 |
858 |
18,47 |
14,9 |
12,9 |
|
|
13,1 |
1093,9 |
961 |
14,9 |
15,6 |
|
|
|
15,6 |
966 |
16,89 |
13,01 |
|
|
|
15,7 |
962,9 |
874 |
15,5 |
|
|
|
|
16,68 |
879 |
18,35 |
|
|
|
|
16,1 |
1071,7 |
982 |
|
|
|
|
|
16,7 |
987 |
|
|
|
|
|
16,8 |
1157 |
|
|
|
|
|
|
16,9 |
|
|
|
|
|
|
17,2 |