Задачи 31-40

Определить набор товаров потребителя (х₁,х₂), макси­мизирующий функцию полезности

при заданном бюджетном ограничении.

Цены товаров р₁, р₂; доход (бюджет) потребителя m, а также параметры с и d функции полезности приведены в таб­лице 4.

Таблица 4

№№ задач	Р1	Р2	т	с	d
31	2	3	36	1/6	5/6
32	3	4	72	2/6	4/6
33	7	10	420	3/6	3/6
34	9	11	594	4/6	2/6
35	4	5	120	5/6	1/6
36	6	7	336	1/8	7/8
37	12	11	1056	2/8	6/8
38	3	9	216	3/8	5/8
39	5	8	320	4/8	4/8
40	9	4	288	5/8	3/8

Задачи 41-50

Найти решение и цену игры, заданной следующей пла­тежной матрицей:

41.	42.		43.
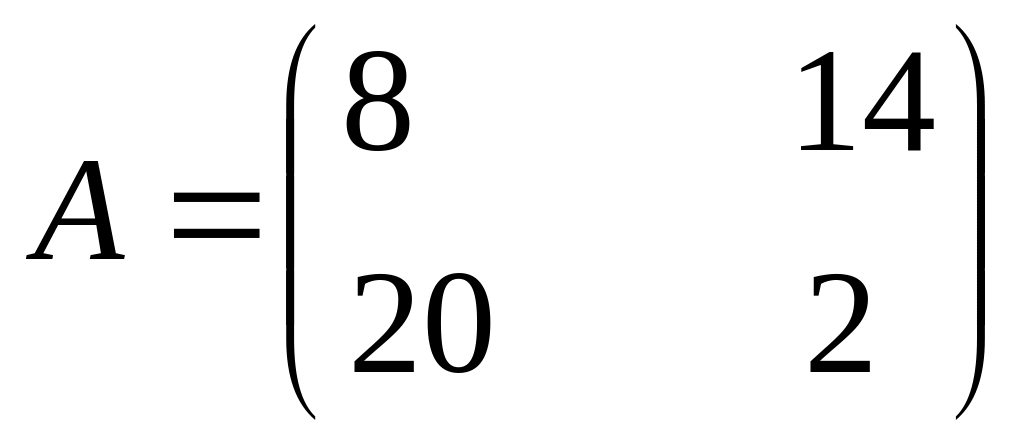
44.	45.		46.
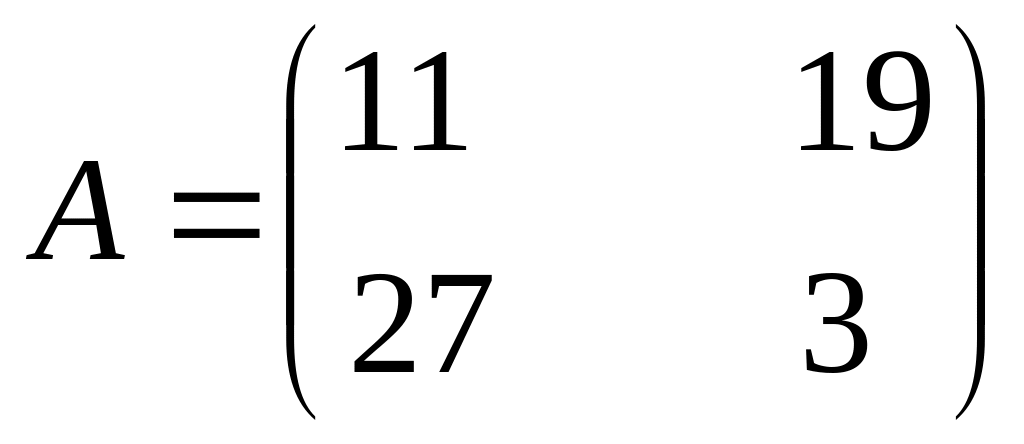
47.	48.		49.
50.

Методические указания

Настоящие указания составлены в соответствии с учебни­ками [1], [2] и [3]:

1. Исследование операций в экономике: Учебное посо­бие / Под ред. Н.Ш. Кремера. - М.: ЮНИТИ-ДАНА, 2006.

2. Высшая математика для экономистов: Учебное посо­бие / Под ред. Н.Ш. Кремера. - М: ЮНИТИ, 2004.

3. Бережная Е.В., Бережной В.И. Математические методы моделирования

экономических систем: Учебное пособие. – М.: Финансы и статистика, 2006

Приведем образец решения и оформления заданий контрольной работы

Задача 1

На изготовление двух видов продукции Р₁ и Р₂ требует­ся три вида сырья S₁, S₂ и S₃ , запасы которого ограничены и составляют соответственно b₁, b₃ и b₂ условных единиц. Коли­чество сырья, необходимое для изготовления единицы каждого из видов продукции дано в таблице5.

Таблица 5

Сырье	Продукция		Запасы сырья
	P1	Р2
S1	a11	a12	b1
S2	a21	а22	b2
S3	a31	а32	b3
Прибыль	C1	C2

Здесь а_ij - количество сырья вида S_j, необходимое для изготовления единицы продукции типа P_j (i=l,2,3; j-1,2). В последней строке указана прибыль (в условных денежных еди­ницах), получаемая от реализации единицы соответствующей продукции (предполагается, что вся выпущенная продукция реа­лизуется). Требуется составить план выпуска продукции, при котором суммарная прибыль от реализации всей продукции была бы максимальной.

Рассмотрим конкретный пример ( таблица 6).

Таблица6

Сырье	Продукция		Запасы сырья
	P1	P2
S1	3	3	15
S2	2	6	18
S3	4	0	16
Прибыль	2	3

Решение

Обозначим искомый план производства через (х₁ ,х₂), где х₁ - количество продукции типа Р₁; х₂ - ко­личество продукции типа Р₂. Составим ограничения задачи. Ог­раничивающим фактором здесь является сырье. Например, на план производства (х₁, х₂) должно истратиться Зх₁ + Зх₂ сы­рья вида S₁, запасы которого равны 15 ед., поэтому должно вы­полняться неравенство

для сырья S₂ и S₃, соответственно, должны выполняться неравен­ства 2х₁ + 6х₂ ≤ 18 и 4х₁ ≤ 16

По смыслу задачи в систему ограничений необходимо включить еще два неравенства

и .

Объединим все неравенства в систему

Эта система носит название системы ограничений задачи.

В качестве целевой функции задачи выступает суммарная прибыль, которая, очевидно, имеет вид

Итак, мы построили математическую модель задачи:

Заметим, что это - задача линейного программирования с двумя переменными. Решим ее графическим методом.

Рассмотрим систему неравенств; множество ее решений называется ОДР - областью допустимых решений или об­ластью допустимых планов.

Построим область решений первого неравенства системы ограничений 3х₁ + 3х₂ ≤ 15. Сначала построим прямую Зх₁ + Зх₂ =15, например, по точкам (0,5), (5,0), которую обозначим цифрой (I). Эта прямая разбивает всю плоскость на две полуплоскости. Для определения полуплоскости решений нашего неравенства возьмем произвольную точку плоскости, не нежащую непрямой Зх₁ +3х₂ = 15, например, (0, 0), и подставим ее координаты в неравенство: 3 · 0 + 3 · 0 ≤ 15. Так как О < 15, то течка (0, 0) лежит в полуплоскости решений нашего неравенства Противоположную полуплоскость мы заштрихуем (см. рис. 1).

Аналогично строим полуплоскости решений остальных неравенств системы ограничений, каждый раз заштриховывая "ненужную" полуплоскость [прямые (II) и (Ш)]. Заметим, что неравенстве х₁ ≥ 0 и х₂ ≥ 0 "выделяют" первый квадрант (заштриховываем левую полуплоскость от прямой x₁=0 нижнюю от прямой х₂ =0). Таким образом, ОДР - это замкну­тый многоугольник OABCD (рисунок1).

Х₂

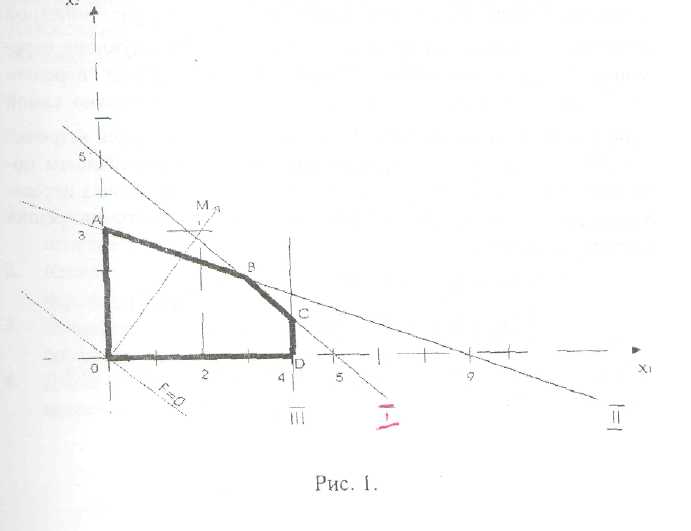
Рисунок 1

Теперь нужно среди точек построенного многоугольника (включая и его границу!) найти такую, в которой целевая функ­ция F(x₁, х₂) = 2х₁ +3х₂ достигает максимального значения. Для этого построим прямую, заданную уравнением 2х₁ + 3х₂ = 0, которая является линией нулевого уровня функ­ции F{x₁, x₂,). Как известно, линии уровней линейной функции образуют на плоскости семейство параллельных прямых, на каж­дой из которых функция принимает постоянное значение. При переходе от одной линии уровня к другой значение функции из­меняется. Направление "наискорейшего" возрастания функции F указывает вектор

(в нашем случае это вектор с началом в начале координат (0, 0) и концом в точке (2, 3), координаты которого в случае линейной функции F равны коэффициентам при соответствующих пере­менных). Для нахождения оптимального плана нужно "передви­гать" линию нулевого уровня функции F параллельно самой себе в направлении вектора М до точки ее "последней встречи" с ОДР. Эта точка (или отрезок прямой) и будет решением по­ставленной задачи. В нашем случае это точка В - точка пересе­чения прямых (I) и (II). Найдем координата этой точки, решив систему уравнений:

→ В(3;2)

Следовательно, усл. ден. ед.

Ответ: для получения суммарной максимальной прибыли нужно выпускать 3 ед. продукции типа P₁ и 2 ед. про­дукции типа P₂. При таком плане прибыль составит 12 ден. ед.

Замечание I: Если требуется найти минимум функции F , то линию нулевого уровня следует передвигать до точки "первой встречи" с ОДР или в направлении, противопо­ложном вектору .

Как правило, задачи, в которых целевая функция представляет собой затраты производства, требуют минимизации этой функции.

Замечание 2: Если на рисунке "не видно" опти­мальной точки, то рекомендуется найти координаты всех вершин многоугольника и посчитать значение функции F в этих точках. Наибольшее (или наименьшее) значение функции F укажет оптимальную точку (или отрезок прямой).

Задача 2

Ниже приведена таблица 7, в которой указаны запасы не­которого груза у поставщиков А₁ , А₂ , А₃ , потребности в этом грузе потребителей В₁ , В₂,, B₃, а также стоимости (тарифы) с₁₁ c₁₂ ,…, c₃₃ перевозки единицы этого груза от каждого поставщи­ка каждому потребителю (тариф c_ij означает стоимость перевоз­ки единицы груза от поставщика A_i потребителю В_j ); величи­ны c_ij указаны в некоторых денежных единицах. Составьте оп­тимальный план перевозок - такой, чтобы все потребители были удовлетворены и при этом стоимость всех перевозок была бы наименьшей.

Таблица 7

Поставщики	Потребители			Запасы
	B1	B2	B3
A1	3	4	1	70
А2	4	1	3	40
A3	2	2	4	80
Потребности	60	90	40	Итого: 190

Решение

1. Составление начального плана перевозок ([1], стр. 129-131).

а) Метод "северо-западного угла".

Заполним клетку а_1] - "северо-западный угол" матрицы перевозок. В нее можно запланировать перевозку 60 единиц гру­за: потребность потребителя В_] равна 60 единицам, а у постав­щика А₁ имеется воз­можность поставить B₁ весь требуемый груз (60 единиц из имеющихся у него 70). При этом 1-й столбец матрицы перевозок будет закрыт, а в пер­вую строку останется в дальнейшем размес­тить перевозку 10 единиц (рисунок 1).

60 - -		10 40 80
90 40

Рисунок 1

Заполняем "северо-западный угол", оставшейся незапол­ненной части таблицы - клетку a₁₂ . В нее можно запланировать перевозку 10 единиц груза, оставшихся у поставщика А_], потре­бителю В₂; при этом все возможности А₁ будут исчерпаны, а В₂ надо будет поставить еще 80 единиц груза. При этом 1-я строка матрицы перевозок будет закрыта (рисунок 2).

60	10 -	40 80
- -
	80 40

Рисунок 2

Снова заполняем "северо-западный угол" незаполненной части таблицы - клетку a₂₂ . В нее можно запланировать перевоз­ку 40 единиц груза, имеющихся у А₂, потребителю В₂; при этом все возможности А₂,будут исчерпаны, а потребителю В₂ надо будет поставить еще 40 единиц груза; 2-я строка матрицы будет закрыта (рисунок 3).

60 -	10 40	80
-
	40 40

Рисунок 3

В оставшейся незаполненной части последней строки матрицы перевозок заполняем сначала "северо-­западный угол" - клетку а₃₂ (в нее ставим, естественно, 40 единиц груза и закрываем 2-й столбец), а затем – оставшуюся клетку a₃₃ (снова "северо-­западный угол" оставшейся незаполнен­ной части таблицы); получаем план перевозок, изображенный на рисунке 4.

60 10 - - 40 - - 40 40

Рисунок 4

Подсчитаем стоимость затрат на перевозки по этому пла­ну. Для этого объем перевозки, указанный в каждой заполненной клетке, надо умножить на тариф этой клетки и сложить все полу­ченные произведения:

Метод "северо-западного угла" очень простой Он никак не учитывает стоимости перевозок. Точно так же можно применять ме­тод "юго-восточного угла" или какого-нибудь другой, важно лишь четко сформулировать правило (алгоритм) составления плана.

б) Метод наименьшей стоимости.

Находим клетку матрицы перевозок с наименьшим тари­фом; таких клеток две: а₂₂ и а₁₃ - тарифы в них равны 1. По­скольку в клетку а₂₂ можно поместить 40 единиц груза (это наи­меньшее из чисел 40 и 90, соответственно запасов А₂ и потребностей В₂), а в клетку а₁₃ - тоже 40 единиц.

Выбираем одну из них произвольно, например, клетку a₁₃, и закрываем 3-й столбец, а у поставщика А₁ оставляем 70 -40 = 30 единиц груза (рисунок 5).

		40	30
		-	40
		-	80
60	90

Рисунок 5

В оставшейся незаполненной части матрицы перевозок наименьший тариф имеет клетка а₂₂. Заполняем ее: ставим перевозку 40, закрываем вторую строку, а потребителю В₂ останется еще по­лучить 50 единиц груза (рисунок 6).

		40	30
-	40	-
		-	80
60	50

Рисунок 6

В оставшейся неза­полненной части мат­рицы перевозок наи­меньший тариф (2

денежные единицы) имеют клетки a₃₁, и а₃₂ - В первую из них помещаем требуемые там 60 единиц груза (во вторую можно поместить лишь 50 единиц- меньше), закрываем первый столбец, уменьшая запасы А₃ до 80 - 60 = 20 единиц груза (рисунок 7)

- 40 - 40 - 60 -	30 20
50

Рисунок 7

Дальше матрица заполняется однозначно - в незаполненные клетки a₁₂ и a₃₂ ста­вим требуемые там 30 и 20 единиц груза соот­ветственно. План со­ставлен (рисунок 8). Под­считаем стоимость за­трат по составленному плану:

30 • 4 + 40 • 1 + 40 • 1 + 60 • 2 + 20 • 2 = 360 (ед.).

- 30 40 - 40 - 60 20 -

Рисунок 8

Метод наименьшей стоимости дал более выгодный план, поэтому будем рассматривать именно его в качестве начального. Отметим два обстоятельства. В обо­их планах оказались заполненными одина­ковое число клеток. Это не случайно. Для невырожденных задач это число равно, как известно из теории, т+п-1 где т и п -размеры матрицы перевозок. В нашем случае т = n = 3 , поэтому должны быть заполнены 3 + 3 — 1 = 5 клеток, что и получилось. "Невырожденость" здесь означала, что на каждом этапе решения мы "закрывали" либо столбец, либо строку матрицы перевозок, но никогда столбец и строку одновременно. Если бы случилась необходимость их одновременного закрытия, нам пришлось бы вводить фиктивную нулевую перевозку, чтобы соблюсти указан­ный принцип. Кроме того, мы решали так называемую "закры­тую" транспортную задачу: сумма запасов поставщиков равня­лась сумме потребностей потребителей; иначе нам тоже пришлось бы вводить либо "фиктивных поставщиков", либо "фик­тивных потребителей". Осталось напомнить, что, очевидно, дос­таточно составить исходный план лишь одним способом; мы привели два способа из методических соображений.

Теперь надо выяснить, оптимален ли план, приведенный на рис. 8. Для этого надо провести оценку каждой свободной клетки, составив для нее цикл, а по нему -знакочередующуюся сумму тарифов клеток, входящих в этот цикл: если эта оценка окажется для какой-то клетки неотрицательной, ее невыгодно включать в новый план, если же она окажется отрицательной, то рассматриваемый план не оптимален и эту клетку целесообразно включить в новый, более выгодный план.

Как только в некотором плане все свободные клетки бу­дут иметь» неотрицательные оценки, мы получим оптимальный план.

Исследование исходного плана на оптимальность (распределительный метод) ([1], стр. 134- 139). Найдем последовательно оценки всех свободных клеток плана перевозок, изображенного на рисунке 8.

Клетка a₁₁. Цикл (рисунок 9). Его оценка

3			4
2			2

Рисунок 9

Клетка a₂₁. Цикл (рисунок 10). Его оценка

					4	1			4	1
4	1				1	3
2	2								2	4

Рисунок 10 Рисунок 11 Рисунок 12

Клетка a₂₃ . Цикл (рисунок 11). Его оценка а₂₃ = 3 -1 + 4-1 =5 >0 .

Клетка a₃₃ Цикл а₃₃ - а₁₃ + а₁₂. – а₃₂ (рисунок 12). Его оценка α₃₃ = 4-1 + 4 – 2 = 5>0

Итак, исследуемый план не оптимален, в новый план сле­дует включить клетку а₁₁ (это единственная свободная слетка с отрицательной оценкой).

Комментарий. Полезно убедиться в единственности (с точностью до направления обхода) цикла для каждой свободной клетки и независимости значения ее оценки от направления об­хода цикла. Иногда возникает недоразумение из-за недопонима­ния такого обстоятельства: мы считаем, что цикл проходит через клетку, если он делает в ней поворот (например, цикл клетки а₁₁ не проходит через клетку а₂₁ , он "перепрыгивает" через нее); поэто­му лучше употреблять такие слова: "клетка входит в цикл" или "принадлежит циклу".

Улучшение плана происходит просто: берем сво­бодную клетку с отрицательной оценкой и производим по ее циклу перемещение поставок так, чтобы не нарушить баланс: в свободную клетку и в те занятые клетки ее цикла, тарифы кото­рых брались при оценке со знаком "+", добавляем некоторое (од­но и то же для всех клеток цикла) количество единиц груза (то есть увеличиваем на это количество запланированные в этих клетках перевозки), а в остальных, клетках цикла на это же коли­чество уменьшаем перевозки. Величина оценки свободной клет­ки имеет экономический смысл: когда она отрицательна, то пока­зывает, насколько выгодней перевозить единицу груза, проделав перемещение поставок по циклу этой клетки, поэтому по циклу надо переместить как можно больше единиц груза. Эта величина ограничена тем, что в тех клеткам, в которых мы уменьшаем по­ставки, не должно остаться отрицательной величины. Значит, мы можем переместить по циклу лишь наименьшую величину еди­ниц груза из тех клеток, тарифы которых входили в оценку со знаком "-". Произведение этой величины на оценку клетки и даст величину выгоды перевозок по новому плану - разности в стои­мости старого и нового планов перевозок.

В нашем случае перемес­тим по циклу клетки a₁₁ 30 единиц груза: в клетки a₁₁ и а₃₂ плана добавляем по 30 единиц груза, и из клеток а₁₂ и а_3] убираем по 30 единиц. Получаем новый, улуч­шенный план, показанный на рисунке 13.

30		40
	40
30	50

3		1
	1	3
2	2

3		1
2		4

Рисунок 13 Рисунок 14 Рисунок 15

Его стоимость на 30 денежных единиц меньше стоимости исходного: (-1)-ЗО=-ЗО; таким образом, по второму плану стои­мость перевозок равна 360- 30 = 330 денежным единицам.

Обязательна проверьте, что стоимость нового плана равна 330 единицам. Тетерь, видимо, становятся понятнее свойства цикла: в него входят ровно по две клетки из столбца или строки из-за того, чтобы при улучшении плана не нарушался баланс: на такую величину мы уменьшили перевозку из одной клетки стро­ки (столбца), на столько же увеличили ее во второй клетке этой строки (столбца), так что общая величина поставок от этого по­ставщика (баланс в строке) или этому потребителю (баланс в столбце) не меняется.

Исследование второго плана на оптимальность. Найдем последовательно оценки всех свободных клеток второго плана.

Клетка a₁₂. Ее только что освободили, так что оценивать ее нецелесообразно.

Клетка а₂₁ .Ее цикл, а зна­чит, и оценка, не изменились; оценка по-прежнему равна 3>0.

К летка а₂₃ (рисунок 14). Его оценка

Клетка a₃₃ . Цикл (рисунок 15). Его оценка

Поскольку во втором плане оценки всех свободных клеток поло­жительны, он оптимален.

Ответ: а₁₁ =30, а₁₃ =40, а₂₂ =40, а₃₁ =30, а₃₂ = 50, а₁₂ = а₂₁ = а₂₃ = а₃₃ = 0; оптимальная стоимость пе­ревозок равна 330 денежным единицам.

Задача 3

Пусть потребительский набор представляет собой вектор x = (х₁ ,х₂), где х₁ - количество первого товара; х₂ -количест­во второго товара. Пусть цена первого товара – р₁, второго – p₂, , а доход (бюджет) потребителя т. Предпочтения потребителя представлены функцией полезности U = U(x₁ , х₂) . Найти оп­тимальный набор потребителя, то есть набор , максими­зирующий функцию полезности U(x₁,x₂) при соблюдении бюджетного ограничения. Конкретные данные взять следующие:

U(x₁, x₂ ) = (функция Кобба-Дугласа) (1)

p₁ =9 ; p₂ =8 ; m = 504.

Решение

Математическая модель задачи

U(x₁ ,x₁)=

9x₁ +8x₂ =504

Это задача нелинейного программирования (задача на ус­ловный экстремум). Поскольку функции полезности определимы лишь с точностью до монотонного преобразования, удобно про­логарифмировать функцию (1) и работать далее с функцией

Итак, имеем следующую задачу

Для решения этой задачи обратимся к методу Лагранжа ([1], стр. 208-209). Построим функцию Лагранжа

Исследуем полученную функцию на безусловный экстре­мум. Для этого вычислим и приравняем нулю ее частные произ­водные по x₁ , х₂, λ :

Составляем систему

Исключая из этой системы, получим

откуда х₁ = 24; х₂ =36.

Таким образом, по необходимому условию существова­ния экстремума дифференцируемой функции получаем стационарную точку М (24; 36) возможного условно­го экстремума функции V(x₁, х₂).

Теперь проверим выполнение достаточного условия существования условного экс­тремума в стационарной точке:

0 р₁ р₂

р₁

обозначим Δ = - _{- определитель,}

р₂

вычисленный при х₁ = х₁⁰, х₂ = х₂⁰.

Если Δ < 0, то функция V (х₁, х₂) имеет в т (х₁⁰, х₂⁰) условный максимум, если Δ > 0 – условный минимум.

Тогда

; при любых х₁ и х₂;

Т ак как

0 9 8

Δ = - 9 - 0 = - -9 +8 =

8 0 -

= - -9 ∙ 9 ∙ - + 8 ∙ 8 ∙ < 0, то т.М (24; 36) – точка условного максимума

функции V (х₁, х₂).

Ответ: оптимальный набор потребителя: х₁⁰ = 24 ед. первого товара, х₂⁰ = 36 ед. второго товара.

Задача 4

Решить игру, заданную следующей платежной матрицей

Решение

Нижняя цена игры а = 4, верхняя β = 5 ,то есть α ≠ β, следовательно, игра седловой точки не имеет ([1], 9.2) и ее решение будем искать в смешанных стратегиях ([1], 9.3). Обозначим через р = (р₁, р₂), q = (q_],q₂)- смешанные стра­тегии первого и второго игроков, соответственно ([1], 9.3).

Как известно , для игры 2 х 2 с платежной матрицей

для определения координат оптимальных смешанных стратегий

Надо решить следующие системы уравнений

и

где ν - цена игры.

Для нашей матрицы А эти системы уравнений приобре­тают вид

и

Решая их, найдем:

Из любого уравнения (кроме третьего) любой системы при уже известных находим цену игры v = 4,5 .

Итак, первый игрок должен применять свои стратегии поровну ("пятьдесят на пятьдесят"), а второй в соотношении 1:3; при этом цена игры составит v = 4,5 (что больше нижней цены игры α = 4 и меньше верхней (β = 5). Заметим, что свои страте­гии в данных соотношениях игроки должны применять «случай­но».

О т в е т: