Усвоить такие дисциплины в вузе, как, например, физику, химию и некоторые другие, где изучаются важнейшие законы естествознания, раскрывается сущность физических, химических и других явлений, невозможно, изучая только теорию этих наук. Нужно пронаблюдать многие явления экспериментально, а для этого необходимо владеть экспериментом, проводить его. Такие навыки приобретаются на лабораторных занятиях, практикумах и требуют дополнительной внеаудиторной подготовки к ним.

Лабораторное занятие, или лабораторная работа – это практическое учебное занятие, организуемое и проводимое в соответствии с правилами и нормами научно-экспериментального исследования (опыта, наблюдения, моделирования), целью и результатом которого является изучение заданными средствами и способами явлений, процессов и иных характеристик лабораторного объекта.

Особенность проведения лабораторного занятия по сравнению с уроком состоит в том, что преподавателю предоставляется возможность индивидуальной работы с каждым студентом. И эту возможность необходимо использовать как можно полнее.

Основными целями проведения лабораторных занятий должны быть:

• углубленное освоение студентами теоретических положений изучаемой дисциплины и получение практических навыков планирования, постановки и решения задач в соответствующей предметной области;

• изучение особенностей строения, состояния, поведения и/или функционирования конкретных объектов исследования;

• освоение приемов, методов и способов выявления, наблюдения, измерения и контроля свойств объекта исследования;

• усвоение приемов, методов и способов обработки, представления и интерпретации результатов проведенных исследований;

• приобретение практических навыков выбора, настройки, регулировки и применения технических средств исследования, наблюдения, контроля, измерения.

Прежде всего, лабораторные занятия преследуют цель – на основе ранее полученных знаний включать учащихся в различные действия для формирования умений и навыков. Студенты, опираясь на полученные знания на уроках, других занятиях, самостоятельно выполняют лабораторные работы, проводят измерения, решают задачи, выполняют упражнения.

Таким образом, лабораторные занятия выполняют следующие функции:

1. образовательная – научить студентов исследовать явления с помощью специальных оборудований;

2. воспитательная – стимулировать потребность в формировании ответственности, коллективизма, социальной коммуникации;

3. развивающая – развивать мышление, внимание, творческие способности.

Лабораторные занятия представляют собой особую конструкцию звена формирования и навыков. Оно строится из следующих этапов:

• организационного – постановки цели и актуализации знаний;

• инструктажа, выполнения лабораторной работы;

• контроля и самоконтроля знаний и способов действий;

• оформления результатов наблюдения;

• подведение итогов;

• определения домашнего задания.

Беря за основание содержание лабораторных работ, выделяют следующие их виды:

• наблюдение и анализ различных явлений, процессов;

• наблюдение и анализ устройства работы оборудования;

• исследование качественных и количественных зависимостей между явлениями;

• изучение устройства и способов пользования контрольно-измерительным инструментом.

Каждое лабораторное занятие должно сопровождаться отчетом, т.к. он является документом, свидетельствующим о выполнении студентом лабораторной работы (ЛР). Отчет должен включать:

• титульный лист, оформленный в соответствии с требованиями;

• цели выполненной ЛР;

• используемые материалы, технические и программные средства;

• термины и определения (при необходимости);

• описание задания (постановка задач, подлежащих выполнению в процессе ЛР, осуществляемая студентом.);

• описание основной части (краткая характеристика объекта исследования; методика или программа ЛР; результаты измерений, наблюдений и расчетов, представленные в форме таблиц, графиков, диаграмм и т.д.);

• обсуждение результатов выполнения ЛР в виде кратких, но принципиально необходимых доказательств, обоснований, разъяснений, анализов, оценок, обобщений и выводов;

• приложения (при необходимости).

В зависимости от особенностей лабораторных занятий или их цикла по указанию преподавателя отчет составляется каждым студентом индивидуально или общий на подгруппу (бригаду) студентов.

Лабораторная работа №1 “ Решение задач линейного программирования с использованием Microsoft Excel”

1. Цель работы

Целью работы является приобретение навыков решения задач линейного и целочисленного программирования в редакторе электронных таблиц Microsoft Excel, входящем в пакет Microsoft Office.

2. Постановка задачи

Найти решение общей задачи линейного программирования, заданной математической моделью в виде целевой функции

(1)

при следующих ограничениях:

(2)

Также решить задачу целочисленного программирования для данной математической модели.

3. Ход решения

3.1 Ввод исходных данных

Для решения поставленной задачи, после запуска табличного редактора Microsoft Excel, необходимо ввести в таблицу необходимые данные. Пример ввода исходных данных для модели (1)-(2) показан на рис. 1.

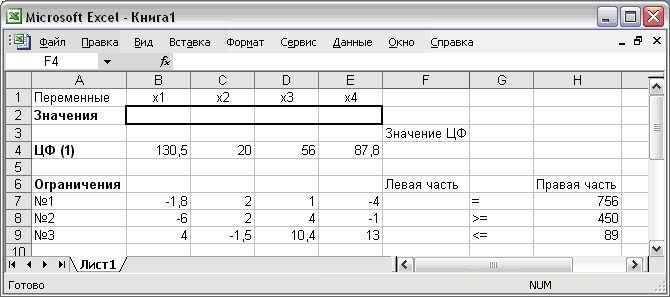
Рис. 1. – Экранная форма задачи линейного программирования

На экранной форме ячейки B2:E2 (на рисунке они выделены рамкой) необходимо оставить пустыми: в них будут отображаться значения переменных x_i после решения. Коэффициенты целевой функции заносятся в ячейки B4:E4 под соответствующими им переменными x_i.

Теперь необходимо ввести зависимости модели в данную экранную форму. В ячейке F4 будет отображаться значение целевой функции (1). Используя обозначения ячеек в Excel, формулу для расчета ЦФ можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных x_i (B2, C2, D2, E2), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B4, C4, D4, E4):

B2·B4 + С·С + D2·D4 + E2·E4.

Чтобы ввести данную формулу в экранную форму необходимо в ячейку F4 ввести следующее выражение: СУММПРОИЗВ($B$2:$E$2;B4:E4). Символ $ перед номером столбца B и строки 2 означает, что при копировании этой формулы в другие места листа Excel номер столбца В и строки 2 не изменится.

Существует другой способ задания функций в Excel с помощью режима "Вставка функций", который можно вызвать из меню "Вставка" или при нажатии кнопки " " на стандартной панели инструментов. Так, например, предыдущую формулу можно задать следующим образом:

• курсор в ячейке со значением целевой функции;

• нажав кнопку " ", вызовите окно "Мастер функций – шаг 1 из 2";

• выберите в окне "Категория" категорию "Математические";

• в окне "Функция" выберите функцию СУММПРОИЗВ;

• в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение $B$2:$E$2, а в строку "Массив 2" – выражение B4:E4 (рис. 2);

• после ввода ячеек в строки "Массив 1" и "Массив 2" в окне "СУММПРОИЗВ" появятся числовые значения введенных массивов, а в экранной форме в ячейке F4 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).

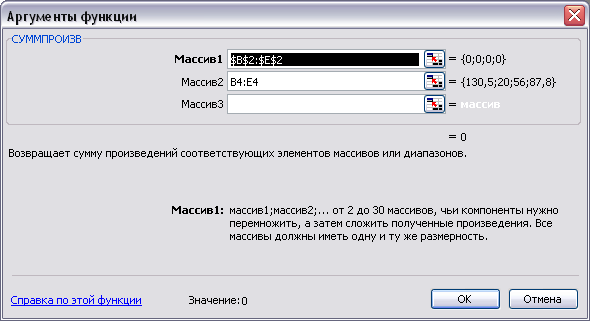
Рис. 2. – Ввод формулы с помощью "Мастера функций"

Далее введем ограничения. Левые части ограничений задачи линейного программирования (2), аналогично целевой функции, представляют собой сумму произведений каждого из значений x_i (ячейки B2:E2) и соответствующих ячеек с коэффициентами для каждого ограничения (ячейки B7:E7, B8:E8, B9:E9 соответственно для каждого ограничения) (рис. 3). Введем в ячейки F7, F8 и F9 соответствующие формулы для расчета левой части каждого ограничения:

1) “=СУММПРОИЗВ($B$2:$E$2;B7:E7)”;

2) “=СУММПРОИЗВ($B$2:$E$2;B8:E8)”;

3) “=СУММПРОИЗВ($B$2:$E$2;B9:E9)”.

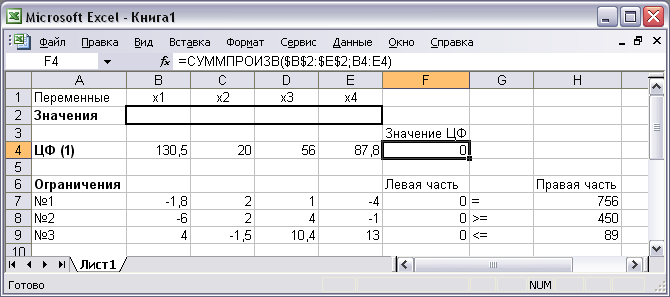
Рис. 3. – Экранная форма задачи после ввода всех необходимых формул

Формулы, задающие левые части ограничений, отличаются друг от друга и от формулы в целевой ячейке F4 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:

• поместить курсор в поле целевой ячейки F4 и скопировать в буфер содержимое ячейки F4 (клавишами "Ctrl+С");

• помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F7, F8 и F9, и вставлять в эти поля содержимое буфера (клавишами "Ctrl+V") (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера).

На экране в полях F7, F8 и F9 появится 0 (нулевое значение).

Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши (или нажатие на клавишу F2) на ячейки с формулами. При этом на экране цветными рамками будут выделяться ячейки, используемые в формуле (рис. 4).

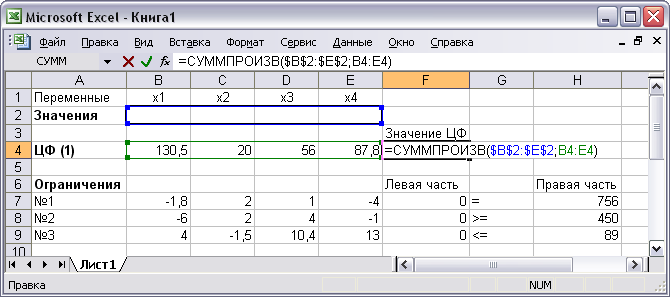
Рис. 4 – Проверка правильности введения формул

3.2 Поиск решения

Решить задачу линейного программирования в Microsoft Excel возможно с помощью инструмента “Поиск решения”. Для этого необходимо в меню “Сервис” выбрать пункт “Поиск решения”. Если его не существует, его необходимо установить. Для этого необходимо выбрать пункт “Надстройки...” в меню “Сервис”, установить галочку напротив необходимой надстройки и нажать кнопку “ОК”.

В окне “Поиск решения” последовательно заполняем необходимые поля:

• поле "Установить целевую ячейку" адрес целевой ячейки F4 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме;

• введите направление оптимизации, щелкнув один раз левой клавишей мыши по селекторной кнопке "максимальному значению";

• в поле "Изменяя ячейки" впишите адреса B2:E2. Необходимые адреса можно вносить в поле "Изменяя ячейки" и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме аналогично целевой функции (рис. 5).

Далее вводим ограничения, для этого (рис. 6):

• нажмите кнопку "Добавить" в окне "Поиск решения" справа от поля “Ограничения”;

• в поле "Ссылка на ячейку" введите адрес ячейки левой части конкретного ограничения, например $F$7;

• в соответствии с условием задачи выберите в поле знака необходимый знак, например “=”;

• в поле "Ограничение" введите адрес ячейки правой части рассматриваемого ограничения, например $H$7;

• аналогично введите ограничения: $F$8>=$H$8, $F$9<=$H$9;

• подтвердите ввод всех перечисленных выше условий нажатием кнопки OK.

Последнее ограничение на не отрицательность переменных x_i будет введено далее.

Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки "Изменить" или "Удалить".

Рис. 5 – Окно "Поиск решения"

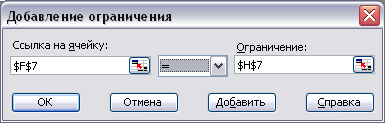
Рис. 6 – Добавление ограничений

Перед решением задачи, предварительно установим конкретные параметры решения задачи оптимизации определенного класса. Для этого необходимо нажать кнопку "Параметры" и заполнить некоторые поля окна "Параметры поиска решения" (рис. 7).

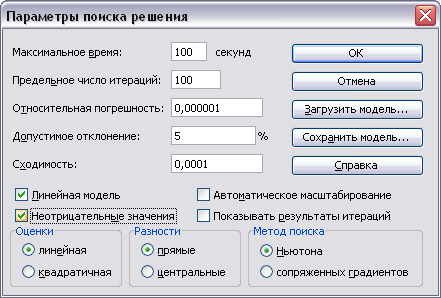
Рис. 7 – Параметры поиска решения

Параметр "Максимальное время" служит для назначения времени (в секундах), выделяемого на решение задачи. Параметр "Предельное число итераций" служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. Параметр "Относительная погрешность" служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.

Параметр "Допустимое отклонение" служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр "Сходимость" применяется только при решении нелинейных задач.

Установка флажка "Линейная модель" обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.

Поставленная задача является линейной задачей линейного программирования, поэтому необходимо отметить галочку "Линейная модель" для более быстрого и точного решения задачи.

Для удовлетворения последнего ограничения (не отрицательности значений x_i) необходимо отметить пункт “Неотрицательные значения”.

Подтвердите установленные параметры нажатием кнопки "OK".