2.3. Эффект масштаба, сетевой эффект и экономические границы монополии

Перейдем теперь к более подробному изучению эффекта мас­штаба и эффекта разнообразия (сети), которые имеют важное значение не только для характеристики поведения неокласси­ческой фирмы, включая установление ею эффективного объе­ма производства и выбор размера производственных единиц, но и для анализа параметров, определяющих рыночные струк­туры.

2.3.1. Эффект масштаба

Как было выше отмечено, при установлении оптимальных размеров производства существенную роль играют свойства про­изводственной функции f(x₁ ...,х_n). Для их характеристики большое значение придается понятию эффект (или экономия от) масштаба (returns to scale). Его значение может быть по­казано на примере функции производственных издержек с дву­мя факторами производства: f(х₁, х₂).

Рассмотрим ситуацию, когда происходит умножение обоих производственных факторов на некоторую положительную ве­личину k (или возрастание их размера в k раз). Возникает во­прос: насколько при этом увеличится объем производства? Эф­фект масштаба отражает определенное свойство технологии фирмы. Если объем производства увеличивается в таком же соотношении, что и факторы производства, то это означает, что эффект масштаба для соответствующей комбинации фак­торов производства является постоянным. В общем виде оп­ределение эффекта масштаба может быть выражено следую­щим образом:

Производственная функция называется однородной (го­могенной) степенью λ, если для некоторой постоянной ве­личины λ и любого положительного числа к выполняется со­отношение:

f(kx₁ kx₂) = k^λf(x₁, х₂).

Говорят, что эффект масштаба возрастает, когда λ > 1; он постоянен, когда λ = 1; и эффект масштаба снижается, если λ < 1.

Показатель степени гомогенности производственной функ­ции λ можно использовать для установления характера взаимо­отношений между производственной функцией и функцией издержек. Здесь могут быть выделены следующие три случая:

1. постоянство экономии от масштаба. f(kx₁, kx₂)=kf(x₁, х₂). В этом случае умножение факторов производства на величину k приводит к пропорциональному же увеличению объемов производства (λ = 1). При таких условиях функция издержек является линейной по отношению к объему. Это оз­начает, что, скажем, увеличение в 2 раза факторов производст­ва приводит к удвоению и объема выпуска. То есть функции средних и предельных издержек идентичны, они обе располо­жены горизонтально;

2. возрастание экономии от масштаба. f(kx₁, kx₂) >kf(x₁, х₂). Умножение факторов производства на величину k приводит к более значительному (по отношению к k) увели­чению объемов производства (здесь λ > 1). Для этого случая характерно снижение функции средних издержек;

3. убывание экономии от масштаба, f (kx₁, kx₂) < < kf(x₁, x₂). Здесь увеличение факторов производства в k раз приводит к непропорционально низкому (по отношению к k) увеличению объемов производства (здесь 0 < λ < 1).

С учетом данного выше определения можно заключить, что возрастающему (убывающему) эффекту от масштаба соответ­ствуют уменьшающиеся (возрастающие) средние издержки.

Вместе с тем для определенных функций издержек при раз­личных объемах производства эффект масштаба может изме­няться. Примеры с различными функциями средних издержек приведены на рис. 2.5. Функция средних издержек может

Рис. 2.5. Примеры различных функций средних издержек в зависимости от эффекта масштаба производства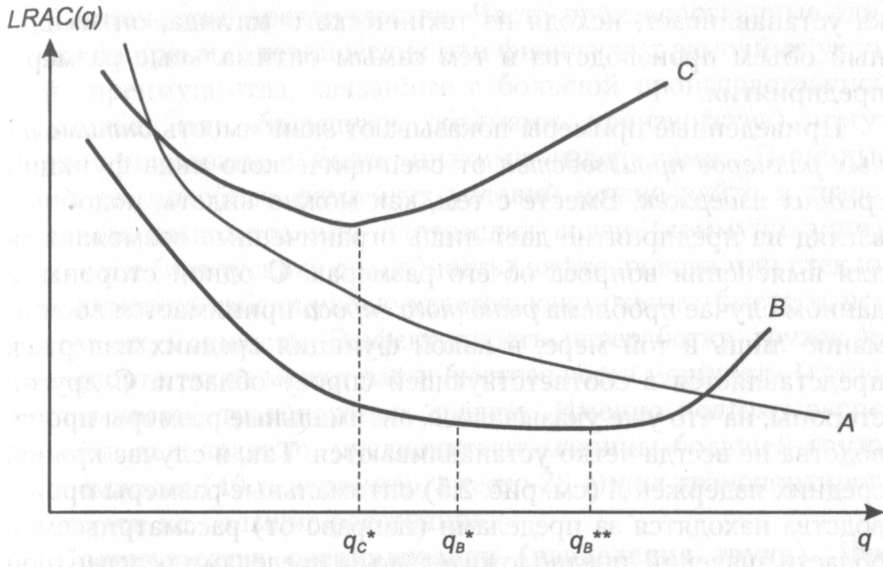

иметь имеет вид А. Здесь эффект масштаба возрастает для всей области значений аргумента функции, соответственно средние издержки монотонно убывают с увеличением объема произ­водства. В этом случае оптимальный размер производства ле­жит за пределами рассматриваемой области значений аргумен­та, поскольку с каждой дополнительной единицей выпуска средние издержки сокращаются.

Для функции средних издержек, имеющей вид В, эффект масштаба вначале возрастает; далее для области q^*_B<q< q^**_B он постоянен, и для области q > q^**_B эффект масштаба снижает­ся. В этом случае, поскольку средние издержки постоянны для целой области q*_B < q < q**_B , оптимальный объем производства и определяемый им оптимальный размер предприятия не мо­жет быть установлен точно.

Функция средних издержек может иметь вид С. В этом слу­чае до уровня q*_c эффект масштаба возрастает, а для уровня производства q > q*_c он сокращается. Средние издержки про­изводства достигают своего минимума в точке q*_c Данная точка устанавливает, исходя из технического взгляда, оптималь­ный объем производства и тем самым оптимальные размеры предприятия.

Приведенные примеры показывают зависимость оптималь­ных размеров производства от специфического вида функции средних издержек. Вместе с тем, как можно видеть, подобный взгляд на предприятие дает лишь ограниченные возможности для выяснения вопроса об его размерах. С одной стороны, в данном случае проблема рыночного спроса принимается во вни­мание лишь в той мере, в какой функция средних издержек представляется в соответствующей спросу области. С другой стороны, на что уже указывалось, оптимальные размеры произ­водства не всегда четко устанавливаются. Так, в случае кривой средних издержек А (см. рис. 2.5) оптимальные размеры произ­водства находятся за пределами (направо от) рассматриваемой области значений, предположительно за пределами релевантной области спроса и соответственно рыночного потенциала. В этом случае минимум средних издержек не может быть достигнут.

В случае кривой В минимум функции средних издержек простирается от точки q*_B, задающей «минимально эффектив­ный масштаб» производства, до точки q**_B («максимально эф­фективного масштаба» производства). Вновь оптимальный размер производства в релевантной области рыночного спроса не может быть точно определен. Только лишь применяемые в учебниках по микроэкономике «U-образные» кривые средних издержек строго определяют оптимальные размеры предпри­ятия в области рыночного спроса, поскольку здесь четко уста­навливается минимум в точке q**_с